Generalised Linear Models

ACTL3142 & ACTL5110 Statistical Machine Learning for Risk Applications

Overview

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

Reading

De Jong & Heller (2008): Chapters 5.1, 5.2, 5.3, 5.4, 5.6, 5.7, 5.9, 5.11

Optional: Haberman & Renshaw (1996)

Introduction to GLMs

Lecture Outline

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

Motivation

We are still trying to explain a response Y via predictors \mathrm{X} \coloneqq \left(1,X_1,X_2,\ldots,X_p \right).
We want the distribution of Y|\mathrm{X} to be flexible.
Solution: Generalised Linear Models, “GLMs”.
These models are characterised by three components:
- Systematic component: a linear function of predictors (as in models we have already seen).
- Stochastic component: a specific probability distribution that describes the response, given the predictors.
- Link function: a function that relates the mean of the response to the systematic component.

GLMs

GLMs have played a key role in the development of statistical modelling (and associated software), and have numerous applications in Actuarial Science.
Linear Regression (under the strong assumptions), Logistic and Poisson Regression are all special cases of GLMs!

GLM: Overview

	Linear Regression	Logistic Regression	Poisson Regression	Generalised Linear Models
Type of Data	Continuous	Binary (Categorical)	Count	Flexible
Use	Prediction of continuous variables	Classification	Prediction of an integer number	Flexible
Distribution of Y\|\mathrm{X}	Normal	Bernoulli (Binomial for multiple trials)	Poisson	Exponential Family
\mathbb{E}[Y\|\mathrm{X}]	\mathrm{X}\boldsymbol{\beta}	\frac{e^{\mathrm{X}\boldsymbol{\beta}}}{1+e^{\mathrm{X}\boldsymbol{\beta}}}	e^{\mathrm{X}\boldsymbol{\beta}}	g^{-1}(\mathrm{X}\boldsymbol{\beta})
Link Function Name	Identity	Logit	Log	Depends on the choice of distribution
Link Function Expression	g(\mu)=\mu	g(\mu) = \ln \left(\frac{\mu}{1-\mu}\right)	g(\mu)=\ln(\mu)	Depends on the choice of distribution

Insurance Applications

Applications are numerous
- Mortality modelling
- Rate making (modelling both claims frequency and severity)
- Loss reserving
Predictors often have a multiplicative effect on the mean of the response (said otherwise, a linear effect on the log-scale), which GLMs can accomodate.
Usually, distributions are not symmetrical and their variance often changes with the mean, e.g.,
- Claim numbers are not Normal, but can be Poisson (or Poisson with over-dispersion).
- Claim amounts are not Normal, but are skewed to the right (for example, shaped like a Gamma).

Non-normality

In linear regression, we usually assume that errors are Normal (or at least, symmetrical). But this means that Y|\mathrm{X} is also normal (or at least, symmetrical).
This is often unrealistic: real data, especially in insurance and finance, is often strongly skewed, heavy-tailed, with bounded support, strictly positive, etc.
GLMs allow the specification of a variety of different distributions for Y|\mathrm{X}:
- Poisson, useful with count data
- Binomial, useful with data on proportions
- Gamma, useful with data showing a constant coefficient of variation
- Exponential, useful with data on time to death (survival analysis)
- And more!

When to use a GLM?

If linear regression does not perform well (poor fit and/or assumptions seem invalid), try GLMs! This can be relevant for example when:

errors are not normal
variance of errors is not constant (against predictors or fitted values)
the response is a “proportion” or a “number of successes out of m trials”
the response is a count (0,1,2,\ldots)
the response is binary (0/1)
the response is continuous but strictly non-negative (linear regression assumes negative values are possible)

Many statistical methods (linear regression, t-test) assume constant variance of errors, which is often untenable. This is an instance where GLMs come in handy.

The components of a GLM

Lecture Outline

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

The components of a GLM

A Generalised Linear Model (GLM) has three components:
1. Systematic component: a linear function of predictors (to capture the location of Y).
2. Stochastic component: a specific probability distribution for Y|\mathrm{X} (to capture the spread of Y around its mean).
3. Link function: a function that specifically links the mean of the response to the systematic component.

The Systematic Component

The systematic component, which we denote \eta_i for short, is “just” a linear function (in its coefficients) of the predictors: \eta_{i} \coloneqq \mathrm{x}_i \boldsymbol{\beta} = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}, where \mathrm{x}_i is the i’th row of the design matrix \boldsymbol{X} and there are p predictor variables (“covariates”) affecting the response.
The mean \mu_i (location) of the response depends on \eta_i, and we assume that for some function g(\cdot), called the link function, g(\mu_i) = \eta_i.
We assume that g(\cdot) is monotone and differentiable (hence continuous), so it has an inverse g^{-1}(\cdot) and we can write \mu_i = g^{-1}(\eta_i).

The Stochastic Component

We now build “spread” around our model for the mean.
For this, we use the exponential dispersion family. We say Y comes from an exponential dispersion family if its density (or mass) has the form f_{Y}(y) = \exp \left[ \frac{y\theta -b\left( \theta \right) }{% \psi }+c\left( y;\psi \right) \right].% \new{\theta\in \Theta,\psi\in \Pi }.
Here \theta and \psi are location and scale parameters, respectively. Note in the book they use a slightly different (but equivalent) representation.
\theta is known as the canonical or natural parameter of the distribution.
b\left( \theta \right) and c\left( y;\psi \right) are known functions (which specify a particular distribution).

Example 1 - Poisson

Let Y be a Poisson(\mu), i.e., f_Y(y) = \frac{\mathrm{e}^{-\mu} \mu^y}{y!}, \quad y\in\{0,1,2,\ldots\}.
Show that Y is in the exponential dispersion family, and identify \theta, \, \psi, \, b(\theta), \, c(y;\psi).

Example 1 - Solution

We use the magic trick x=\mathrm{e}^{\ln(x)} to put everything inside the exponential: \begin{align*} f_Y(y) &=\mathrm{e}^{-\mu} \mathrm{e}^{\ln(\mu^y)} \mathrm{e}^{-\ln(y!)} \\ & = \exp \left(y\ln(\mu)-\mu -\ln(y!) \right) \end{align*}
Hence, we identify that \theta=\ln(\mu).
Equivalently, \mu=\mathrm{e}^{\theta}, and therefore b(\theta)= \mathrm{e}^{\theta}.
\psi=1.
c(y;\psi)=-\ln(y!).

Example 2 - Gamma

The gamma(\alpha,\beta) distribution belongs to the exponential dispersion family. Its density is \begin{align*} f(y) &= \frac{\beta^\alpha y^{\alpha-1}\mathrm{e}^{-\beta y}}{\Gamma(\alpha)}&= \exp\left( -\ln\Gamma(\alpha)+\alpha\ln\beta+(\alpha-1)\ln y-\beta y\right) \end{align*}
Because \theta is a location parameter, it should depend on both \alpha and \beta (since the mean of the Gamma is \alpha/\beta). This motivates us to write everything inside the exponential as \begin{align*} &= \frac{-\frac{\beta}{\alpha}y + \ln \beta}{\frac{1}{\alpha}} -\ln\Gamma(\alpha)+(\alpha-1)\ln y \\ &= \frac{-\frac{\beta}{\alpha}y + \ln \left(\beta \frac{\alpha}{\alpha} \right)}{\frac{1}{\alpha}} -\ln\Gamma(\alpha)+(\alpha-1)\ln y \\ &= \frac{-\frac{\beta}{\alpha}y + \ln \left(\frac{\beta}{\alpha} \right)}{\frac{1}{\alpha}} + \frac{\ln \alpha}{\frac{1}{\alpha}} -\ln\Gamma(\alpha)+(\alpha-1)\ln y \\ \end{align*}

\begin{align*} &= \frac{ -\frac{\beta}{\alpha}y-\left(-\ln\left(\frac\beta\alpha\right)\right) }{ \frac 1\alpha}+\frac{\ln \frac1{1/\alpha}}{\frac1{\alpha}}-\ln\Gamma\left(\frac1{1/\alpha}\right)+\left(\frac1{1/\alpha}-1\right)\ln y \\ &= \exp\left( \frac{y\theta-b(\theta)}{\psi}+c(y;\psi)\right) \end{align*}

This shows that

\theta = -\frac{\beta}{\alpha}, \quad \psi = \frac1\alpha, \quad b(\theta) = -\ln(-\theta),

c(y;\psi) = \frac{\ln\frac1\psi}{\psi}+\left(\frac1\psi-1\right)\ln y-\ln\Gamma\left(\frac1\psi\right).

Members of the Exponential Dispersion Family

Normal N\left( \mu ,\sigma ^{2}\right) with \theta = \mu and \psi = \sigma^2.
Gamma(\alpha, \beta) with \theta = -\beta/\alpha and \psi = 1/\alpha .
Inverse Gaussian(\mu, \lambda) with \theta = -\frac{1}{2\mu^2} and \psi = 1/\lambda.
Poisson(\mu) with \theta = \ln \mu and \psi = 1.
Binomial(m, p) with \theta = \ln \left[p/\left( 1-p\right) \right] and \psi = 1.
Negative Binomial(r, p) with \theta = \ln (1-p) and \psi = 1.

Some Properties of the exponential family

It can be shown that the moment generating function can be expressed as M_{Y}(t) = \mathbb{E}\left( \mathrm{e}^{tY}\right) = \exp \left[\frac{b\left( \theta +t\psi \right) -b\left( \theta \right) }{\psi }\right] .
The cumulant generating function immediately follows: \kappa_Y(t) = \ln M_Y(t) = \frac{b(\theta +t \psi) -b(\theta)}{\psi}. which can be used to determine
- mean: \kappa_1 = \left. \frac{\partial \kappa_{Y}(t)}{\partial t}\right\vert_{t=0} = \color{red}{b^{\prime}(\theta) = \mathbb{E}(Y)} = \mu
- variance: \kappa_2 = \left. \frac{\partial^{2} \kappa_{Y}(t)}{\partial t^{2}}\right\vert_{t=0} = \color{red}{\psi b^{\prime \prime}(\theta) = \text{Var}(Y)}

Expected value (“mean”)

Since \mu = b^\prime(\theta), we can express \mu as function of the location parameter \theta.
But conversely, as \theta is “just” a parameter of the distribution of Y, we can find the \theta that yields any \mu.
Hence, we sometimes write \theta = \theta(\mu), which you can understand as “the \theta that is required for Y to have a mean \mu”.
Exercise: for a Gamma(\alpha,\beta) random variable, find \theta(\mu).

Solution

From the good work we’ve done before, the density can be written as \begin{aligned} f(y)&= \exp\left(\frac{y\theta-b(\theta)}{\psi}+c(y;\psi)\right) \end{aligned} where \theta = -\frac{\beta}{\alpha}, \psi = \frac1\alpha, b(\theta) = -\ln(-\theta),
Then,

\mu = \mathbb{E}[Y] = b^\prime(\theta) = -\frac1{\theta}.

\implies \theta = \theta(\mu) = -\frac1\mu.

List of distributions and their \theta(\mu)

Normal N(\mu, \sigma^2): \theta = \mu.
Gamma(\alpha, \beta): \theta = -\beta/\alpha = -\frac{1}{\alpha/\beta} and hence \theta(\mu) = -\frac{1}{\mu}.
Inverse Gaussian(\mu, \lambda): \theta = -\frac{1}{2\mu^2}.
Poisson(\mu): \theta = \ln \mu.
Binomial(m, p):

\theta = \ln[p/(1-p)] = \ln[mp/(m-mp)],and hence \theta(\mu) = \ln[\mu/(m-\mu)].

Negative Binomial(r, p):

\theta = \ln(1-p) = \ln\left((1-p)\cdot\frac{r}{p}\cdot\frac{p}{r}\right),and hence \theta(\mu) = \ln(\mu p/r).

Variance Function

The variance is sometimes expressed as \text{Var}(Y) = \psi V(\mu), where V(\mu) = b^{\prime \prime}\bigl( \theta(\mu) \bigr) is called the variance function.

Examples

Normal N(\mu, \sigma^{2}) with V(\mu) = 1
Gamma(\alpha, \beta) with V(\mu) = \mu^2
Inverse Gaussian(\mu, \lambda) with V(\mu) = \mu^3
Poisson(\mu) with V(\mu) = \mu
Binomial(m, p) with V(\mu) = \mu (1-\mu/m)
Negative Binomial(r, p) with V(\mu) = \mu (1+\mu/r)

Mean-variance relationship

In linear regression, a central assumption is constant variance (top left graph).
Count data: response is an integer, lots of zeros—variance may increase linearly with mean (top right).
Proportion data: count of number of events out of “trials”, variance will have inverted U-shape (bottom left).
If response follows Gamma distribution (e.g. time-to-death data), variance increases faster than linearly with mean (bottom right).

Example

Show that the variance function of a Gamma(\alpha, \beta) is V(\mu) = \mu^2.

Answer:

f(y) = \exp\left( \frac{y\theta-b(\theta)}{\psi}+c(y;\psi)\right) where \theta = -\frac{\beta}{\alpha}, \psi = \frac1\alpha, b(\theta) = -\ln(-\theta).

Note that \mu = \mathbb{E}[Y] = b^\prime(\theta) = -\frac1{\theta}, and therefore \theta = -\frac1{\mu}. So V(\mu) = b^{\prime \prime}(\theta) = \frac1{\theta^2} = \mu^2.

The link between both components

Recall that the mean \mu_i is connected to the linear predictor \eta_i = \mathrm{x}_i\boldsymbol{\beta} through g(\mu_i) = \eta_i \quad \iff \quad \mu_i = g^{-1}(\eta_i), where g(\cdot) is called the link function.
If we use the specific choice of link function g(\mu) \equiv \theta(\mu), we say we have a canonical (or natural) link function. In that case, \theta_i = \eta_i, i.e., the location parameter is exactly the linear function of predictors.
From De Jong & Heller (2008), “[c]hoosing the canonical link g corresponding to a response distribution f simplifies estimation, although with modern computing this is no longer an overriding consideration”.

Canonical Link Functions

Some canonical links are:

Distribution	Canonical Link g\left( \mu \right)	Called
Normal	g(\mu) = \theta(\mu) = \mu	Identity
Poisson	g(\mu) = \theta(\mu) = \ln \mu	Log link
Binomial	g(\mu) = \theta(\mu) = \ln \left(\frac{\mu }{m-\mu }\right)	Logit
Gamma	g(\mu) = \theta(\mu) = -1/\mu	Reciprocal

Summary of GLM components

A GLM models an n-vector of independent response variables, \boldsymbol{y}, using

A systematic component: \eta_{i} = \mathrm{x}_i \boldsymbol{\beta} = \beta_0 + \beta_1 x_{i1} + \cdots + \beta_p x_{ip}, the linear predictors with \boldsymbol{\beta} = (\beta_0, \beta_1,\ldots,\beta_p) regression parameters.
A stochastic component: for each observation y_{i} we use an exponential dispersion model f(y_i;\theta_i) = \exp \left[ \frac{y_{i}\theta_{i}-b\left( \theta _{i}\right) }{\psi }+c\left( y_{i};\psi \right) \right] where \theta _{i} is the canonical parameter, \psi is a scale parameter and function b(\cdot) and c(\cdot, \cdot) are known functions.
A parametric link function: the link function g(\mu_i) = \eta_i=\mathrm{x}_i\beta combines the linear predictor with the mean \mu_i=\mathbb{E}[Y_i]. The link is called canonical if \theta _{i}=\eta_i.

Fitting a GLM

Lecture Outline

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

Procedure

Constructing a GLM consists of the following steps:

Choose a response distribution f_Y and hence choose b(\theta).
Choose a link function g(\mu).
Choose explanatory variables \mathrm{X} in terms of which g(\mu) is to be modeled.
Collect observations y_1,\cdots,y_n on the response Y and corresponding values \mathrm{x}_1,\ldots,\mathrm{x}_n on the explanatory variables \mathrm{X}.
Fit the model by estimating \boldsymbol{\beta} and, if unknown, \psi.
Given the estimate of \boldsymbol{\beta}, generate predictions (or fitted values) of y for different values of \mathrm{X} and examine how well the model fits.
The estimated values of \boldsymbol{\beta} (and associated confidence intervals) are used to assess whether given predictors are important in explaining Y.

Maximum Likelihood Estimation

The parameters in a GLM are estimated using maximum likelihood.
For each observation y_{i}, the contribution to the likelihood is f(y_i; \theta_i) = \exp \left[ \frac{y_{i}\theta_{i}-b\left( \theta _{i}\right) }{\psi }+c\left( y_{i};\psi\right) \right].
Given a vector \boldsymbol{y} of n observations of Y, we want to find the MLE of \boldsymbol{\beta}. Recall that \theta_i depends on \boldsymbol{\beta} via

\theta_i = \theta_i(\mu_i) = \theta_i(g^{-1}(\mathrm{x}_i \boldsymbol{\beta})).

Since the y_i are mutually independent, the likelihood of \boldsymbol{\beta} is

L(\boldsymbol{\beta}) = \prod_{i=1}^n f(y_i; \theta_i).

Maximum Likelihood Estimation

For n independent observations y_{1}, y_{2}, \dots, y_{n}, we have

L(\boldsymbol{\beta}) \equiv L(\boldsymbol{y}; \boldsymbol{\mu}) = \prod_{i=1}^{n} \exp \left[ \frac{y_{i}\theta _{i}-b(\theta_i) }{\psi} + c\left( y_{i};\psi \right) \right].

We take the log to obtain the log-likelihood as

\ell(\boldsymbol{y}; \boldsymbol{\mu}) = \sum_{i=1}^n \left[ \frac{y_i \theta_i - b(\theta_i)}{\psi} + c(y_i; \psi) \right].

Example

Consider a GLM model with Gamma distribution, canonical link and known \psi. The density of the response variable is \begin{aligned} f(y)&= \exp\left( \frac{y\theta-b(\theta)}{\psi}+c(y;\psi)\right) \end{aligned} with b({\theta}) = -\ln(-\theta).
With canonical link, we have \theta_i = \theta(\mu_i) = g(\mu_i) = \mathrm{x}_i \boldsymbol{\beta}.
Using the log-likelihood \ell(\boldsymbol{y}; \boldsymbol{\mu}) = \sum_{i=1}^n \left(\frac{y_i \theta_i - b(\theta_i)}{\psi} + c(y_i; \psi)\right), can you find the p+1 equations that, if solved, will yield the MLE of \boldsymbol{\beta}?

Solution

First, note that

\frac{\partial}{\partial \beta_j} \ell (\boldsymbol{y} ; \boldsymbol{\mu}) = \sum_{i=1}^n \frac{y_i - b^\prime(\theta_i)}{\psi} \frac{\partial \theta_i}{\partial \beta_j}

Then, recall that \theta_i=\mathrm{x}_i \boldsymbol{\beta}, so

\begin{align*} \frac{\partial \theta_i}{\partial \beta_0} & = 1 \\ \frac{\partial \theta_i}{\partial \beta_j} & = x_{ij} \quad \text{for } j=1,2,\ldots,p. \end{align*}

We also have b^\prime(\theta_i)=-1/\theta_i.

Hence, the derivative with respect to \beta_0 is

\frac{\partial}{\partial \beta_0} \ell (\boldsymbol{y} ; \boldsymbol{\mu}) = \sum_{i=1}^n \frac{y_i - \left(-\frac{1}{\theta_i}\right)}{\psi} = \sum_{i=1}^n \frac{y_i + \frac{1}{\mathrm{x}_i \boldsymbol{\beta}}}{\psi}

All other derivatives (for j=1,2,\ldots,p) are

\frac{\partial}{\partial \beta_j} \ell (\boldsymbol{y} ; \boldsymbol{\mu}) = \sum_{i=1}^n\frac{y_i - \left(-\frac{1}{\theta_i}\right)}{\psi} x_{ij} = \sum_{i=1}^n\frac{y_i + \frac{1}{\mathrm{x}_i \boldsymbol{\beta}}}{\psi} x_{ij}

Setting those p+1 equations to 0 and solving for \beta_0, \beta_1, \ldots, \beta_p will yield the MLEs of \boldsymbol{\beta}.

R demo with insurance data

Lecture Outline

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

Case Study: Motor claims illustration

Consider the data used in McCullagh & Nelder (1989), p.299, related to motor claims.
In this case study, the response is the average claim in specific groups.
There are three factors used:
- policyholder age (PA), with 8 levels, 17-20, 21-24, 25-29, etc.
- car group (CG), with 4 levels, A, B, C, and D.
- vehicle age (VA), with 4 levels, 0-3, 4-7, 8-9, 10+
There are a total of 123 different cells of data (we remove 5 categories with no claims).

Case Study: Motor claims illustration

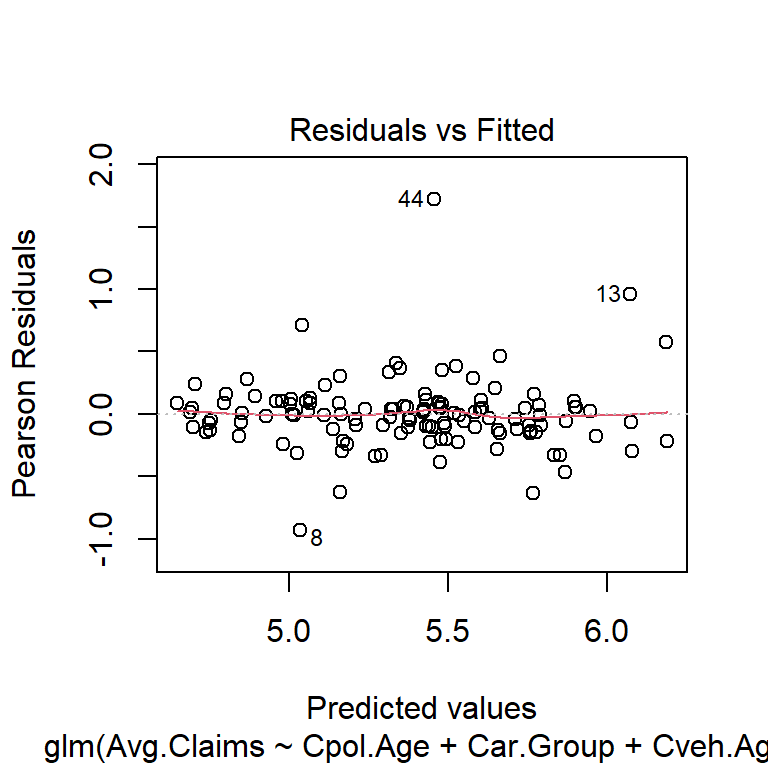
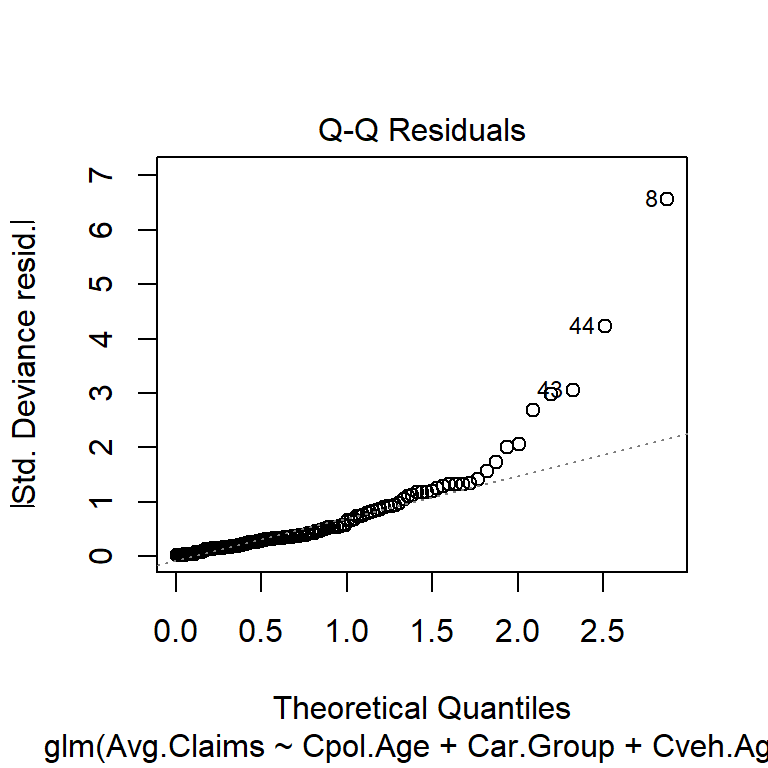
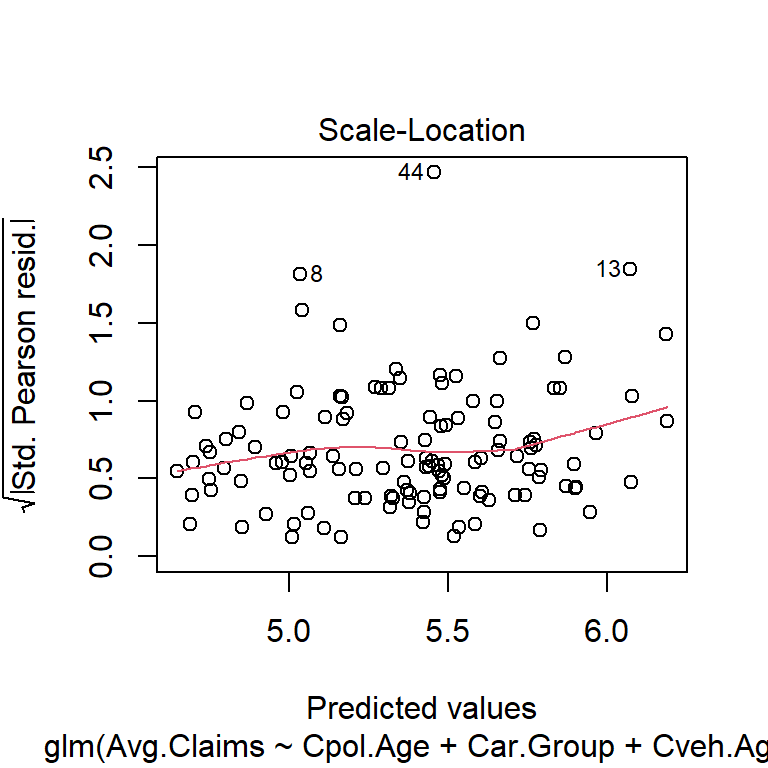
library(tidyverse)

PCarIns <- read_csv("PrivateCarIns1975-Data.csv")
PCarIns <- PCarIns %>% filter(Numb.Claims>0) # remove the 5 categories with no claims

str(PCarIns)

spc_tbl_ [123 × 7] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
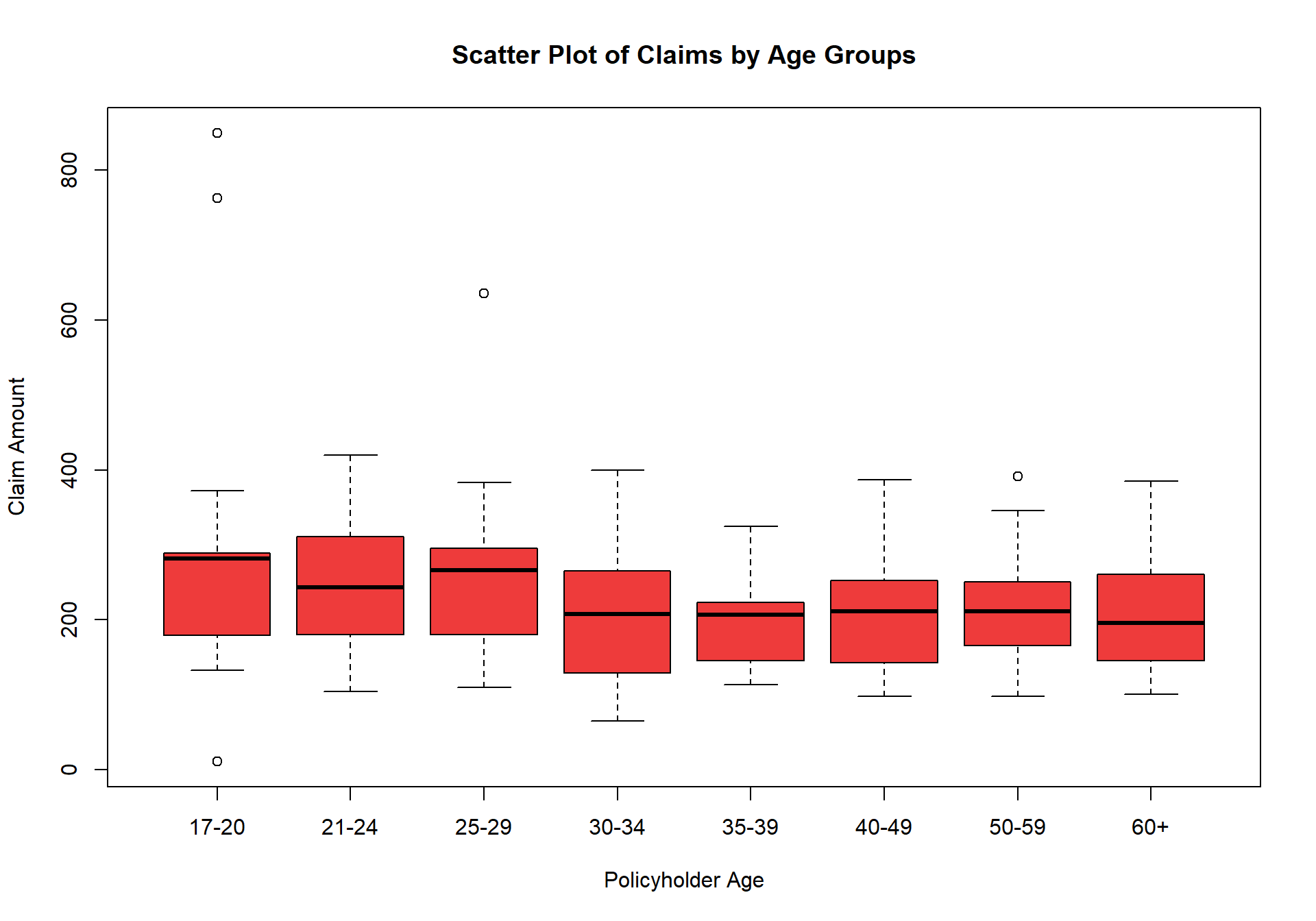
 $ Pol.Age    : num [1:123] 1 1 1 1 1 1 1 1 1 1 ...
 $ Cpol.Age   : chr [1:123] "17-20" "17-20" "17-20" "17-20" ...
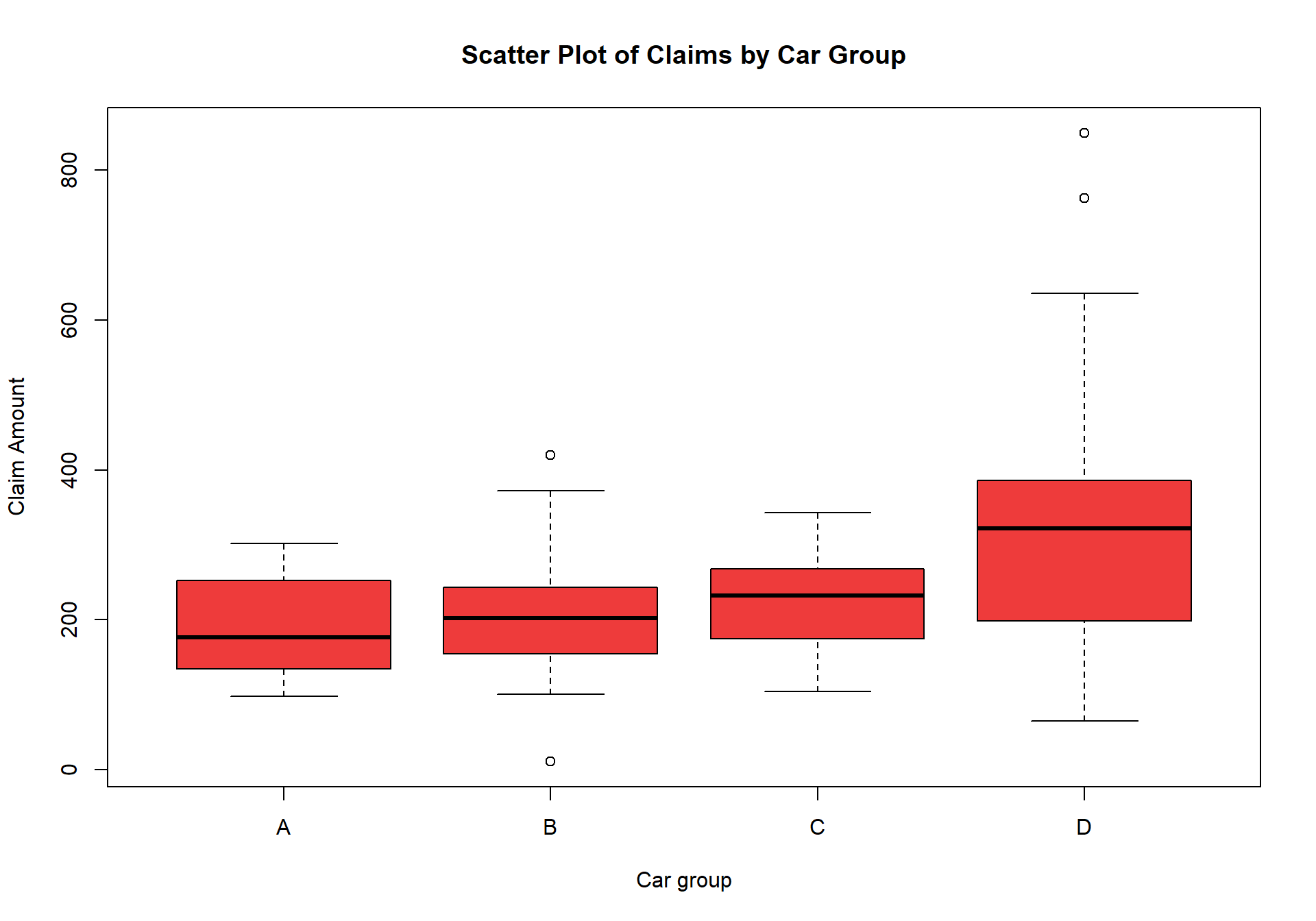
 $ Car.Group  : chr [1:123] "A" "A" "A" "A" ...
 $ Veh.Age    : num [1:123] 1 2 3 4 1 2 3 4 1 2 ...
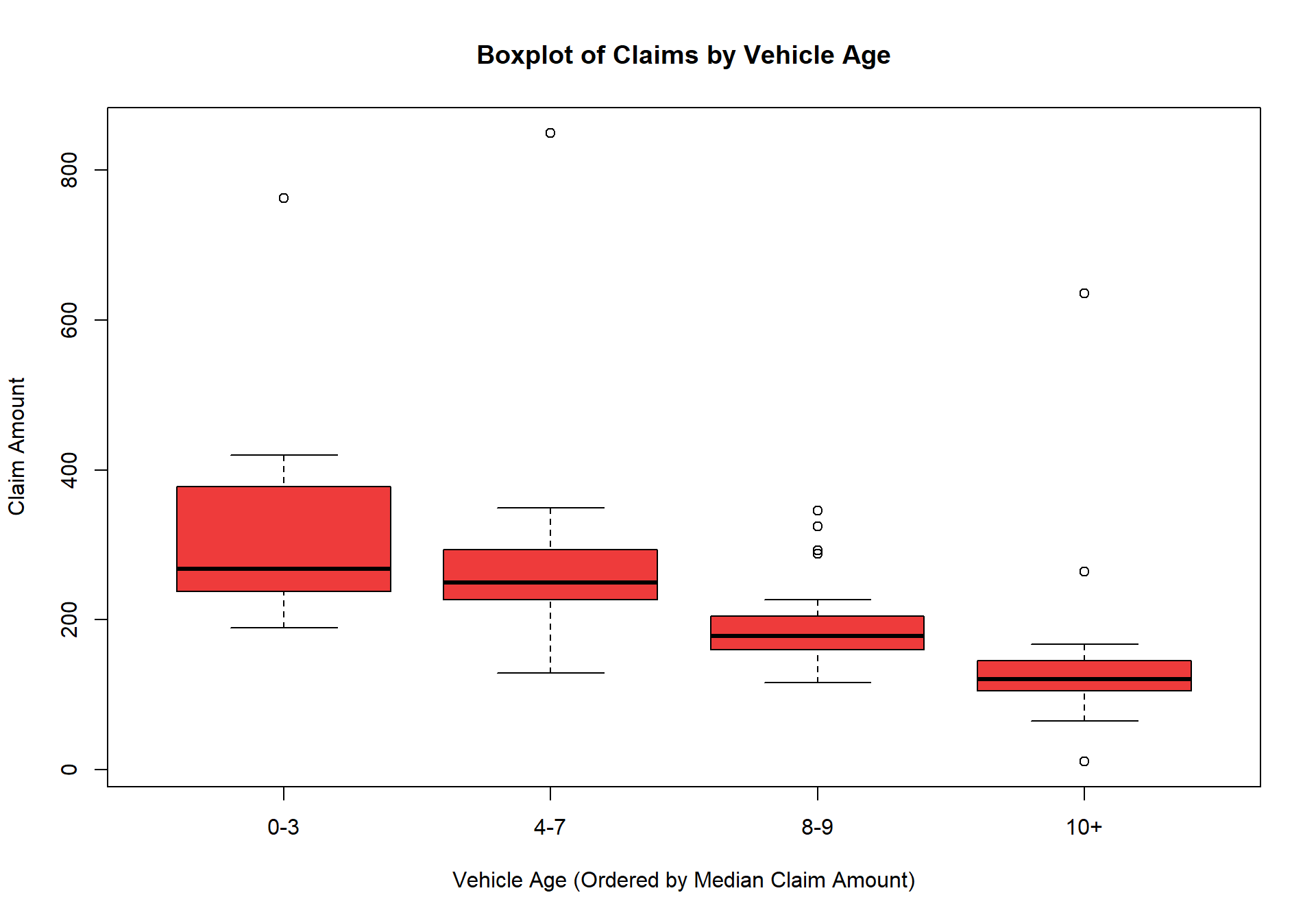
 $ Cveh.Age   : chr [1:123] "0-3" "4-7" "8-9" "10+" ...
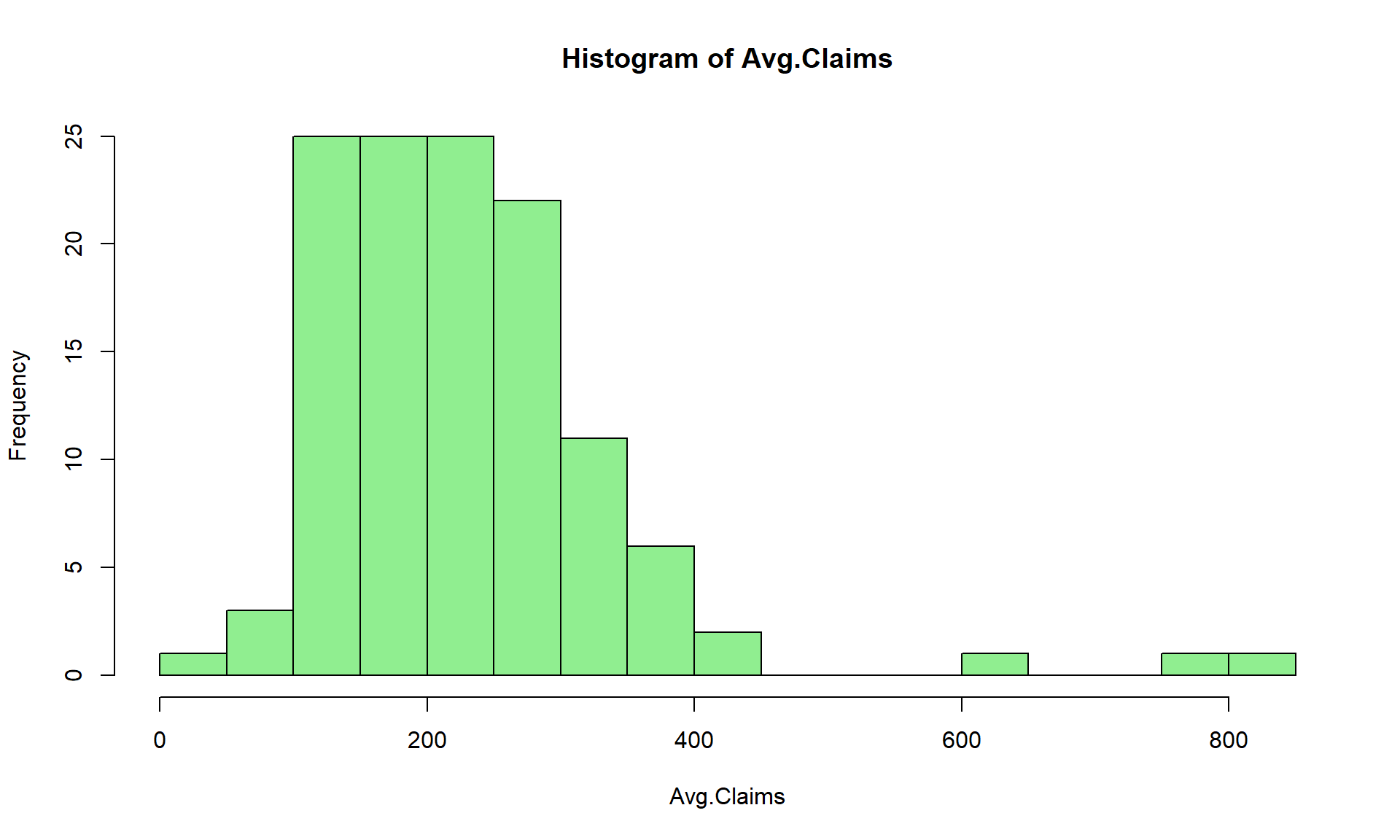
 $ Avg.Claims : num [1:123] 289 282 133 160 372 249 288 11 189 288 ...
 $ Numb.Claims: num [1:123] 8 8 4 1 10 28 1 1 9 13 ...
 - attr(*, "spec")=
  .. cols(
  ..   Pol.Age = col_double(),
  ..   Cpol.Age = col_character(),
  ..   Car.Group = col_character(),
  ..   Veh.Age = col_double(),
  ..   Cveh.Age = col_character(),
  ..   Avg.Claims = col_double(),
  ..   Numb.Claims = col_double()
  .. )
 - attr(*, "problems")=<externalptr>

# convert to categorical
PCarIns <-  PCarIns %>% 
  mutate(Cpol.Age = factor(Cpol.Age),
         Car.Group = factor(Car.Group),
         Cveh.Age = factor(Cveh.Age))

Case Study: Motor claims illustration

Show code for Figure

#par(mfrow=c(1,2)) # Set up the plotting area to have 1 row and 2 columns
hist(PCarIns$Avg.Claims, main="Histogram of Avg.Claims", col="lightgreen", 
     breaks="FD", xlab="Avg.Claims")

Show code for Figure

plot(x = PCarIns$Cpol.Age,y = PCarIns$Avg.Claims, 
     xlab = "Policyholder Age", ylab = "Claim Amount",  main="Scatter Plot of Claims by Age Groups", col="brown2")

Show code for Figure

plot(x = PCarIns$Car.Group, y = PCarIns$Avg.Claims, 
     xlab = "Car group", ylab = "Claim Amount", main="Scatter Plot of Claims by Car Group", col="brown2")

Show code for Figure

boxplot(Avg.Claims ~ reorder(Cveh.Age, -Avg.Claims, median), data = PCarIns,
        xlab = "Vehicle Age (Ordered by Median Claim Amount)", 
        ylab = "Claim Amount", 
        main = "Boxplot of Claims by Vehicle Age", 
        col="brown2")

How do we model the relationship between claims and the covariates?

Case Study: Motor claims illustration - Gamma GLM

pcarins.glm <- glm(Avg.Claims~ Cpol.Age + Car.Group + Cveh.Age,
                   family=Gamma(link="log"),  data = PCarIns)
summary(pcarins.glm)


Call:
glm(formula = Avg.Claims ~ Cpol.Age + Car.Group + Cveh.Age, family = Gamma(link = "log"), 
    data = PCarIns)

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.711672   0.103851  54.999  < 2e-16 ***
Cpol.Age21-24 -0.108184   0.114564  -0.944  0.34710    
Cpol.Age25-29  0.005219   0.113187   0.046  0.96331    
Cpol.Age30-34 -0.288110   0.113187  -2.545  0.01231 *  
Cpol.Age35-39 -0.331051   0.114564  -2.890  0.00465 ** 
Cpol.Age40-49 -0.280799   0.113187  -2.481  0.01464 *  
Cpol.Age50-59 -0.238162   0.113187  -2.104  0.03767 *  
Cpol.Age60+   -0.283549   0.113187  -2.505  0.01372 *  
Car.GroupB     0.057942   0.075458   0.768  0.44422    
Car.GroupC     0.154767   0.076126   2.033  0.04448 *  
Car.GroupD     0.472303   0.078509   6.016 2.44e-08 ***
Cveh.Age10+   -0.735519   0.078509  -9.369 1.18e-15 ***
Cveh.Age4-7   -0.111420   0.075458  -1.477  0.14267    
Cveh.Age8-9   -0.422360   0.076126  -5.548 2.04e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Gamma family taken to be 0.09110331)

    Null deviance: 27.839  on 122  degrees of freedom
Residual deviance: 11.265  on 109  degrees of freedom
AIC: 1398.1

Number of Fisher Scoring iterations: 7

Diagnostics and measures of model fit

Lecture Outline

Introduction to GLMs
The components of a GLM
Fitting a GLM
R demo with insurance data
Diagnostics and measures of model fit

The “Null Model” and “Saturated Model”

With a GLM we estimate Y_i\, by \,\hat{\mu}_i.
For n data points, we can estimate up to n parameters.
Null model: the systematic component is a constant term only. \hat{\mu}_i=\bar{y},\quad \text{for all} \quad i = 1, 2, \dots, n
Only one parameter \implies model is much too simple, or “underfitting”.
Saturated (or “full”) model: each observation has its own parameter. \hat{\mu}_i = y_i,\quad \text{for all} \quad i = 1, 2, \dots, n
Model is “perfect” on training data… but useless for inference/predictions \implies model is much too complex, or “overfitting”.

Log-likelihood in the Saturated Model

The log-likelihood in the saturated model is \ell(\boldsymbol{y}; \boldsymbol{y}) = \sum_{i=1}^n \left[ \frac{y_i \widetilde{\theta}_i - b\bigl(\widetilde{\theta}_i\bigr)}{\psi} + c(y_i; \psi) \right] where \widetilde{\theta}_i are the canonical parameter values yielding \mu_i = y_i for all i = 1, 2, \dots, n.

Deviance and Scaled Deviance

We use the notation \widehat{\boldsymbol{\mu}} to mean all MLEs of a chosen model.
One way of assessing the fit of a given model is to compare it to the model with the “closest” possible fit: the saturated model. The likelihood ratio criterion does just this: \begin{aligned} -2\ln \left[ \frac{L(\boldsymbol{y}; \widehat{\boldsymbol{\mu}})}{L(\boldsymbol{y}; \boldsymbol{y})} \right] &= 2 [ \ell(\boldsymbol{y}; \boldsymbol{y}) - \ell(\boldsymbol{y}; \widehat{\boldsymbol{\mu}}) ] = 2\sum_{i=1}^n \left[\frac{y_{i}( \widetilde{\theta}_i - \widehat{\theta}_i)}{\psi}-\frac{b(\widetilde{\theta}_i) -b(\widehat{\theta}_i)}{\psi}\right] \\ &= \frac{D(\boldsymbol{y}, \widehat{\boldsymbol{\mu}})}{\psi} \end{aligned}
D(\boldsymbol{y}, \widehat{\boldsymbol{\mu}}) is called the deviance and D(\boldsymbol{y}, \widehat{\boldsymbol{\mu}})/\psi the scaled deviance.
Deviance plays a similar role for GLMs than RSS plays for linear regression (under which deviance is RSS).

Example

Recall that for a Gamma(\alpha,\beta), \, \theta=-1/\mu and b(\theta)=-\ln(-\theta).
Then, the scaled deviance of the Gamma is

\begin{aligned} -2 \ln \left[ \frac{L(\boldsymbol{y}; \widehat{\boldsymbol{\mu}})}{L(\boldsymbol{y}; \boldsymbol{y})}\right] &= 2 \sum_{i=1}^n \left[ \frac{y_i (\widetilde{\theta}_i - \widehat{\theta}_i)}{\psi} - \frac{b(\widetilde{\theta}_i) - b(\widehat{\theta}_i)}{\psi}\right] \\ &= 2 \sum_{i=1}^n \left[ \frac{-1 + y_i \cdot 1/\widehat{\mu}_i}{\psi} - \frac{- \ln (1/y_i) + \ln(1/ \widehat{\mu}_i)}{\psi} \right] \\ &= \frac{2}{\psi} \sum_{i=1}^n \left[ \frac{y_i - \widehat{\mu}_i}{\widehat{\mu}_i} - \ln ( y_i/\widehat{\mu}_i) \right] . \end{aligned}

Exponential Dispersions and their Deviances

Dropping the subscript i = 1,2,\dots,n, deviances are:

Distribution	Deviance D(y,\hat{\mu})
Normal	\sum (y-\hat{\mu})^2
Poisson	2\sum [y\ln(y/\hat{\mu}) - (y-\hat{\mu})]
Binomial	2\sum [y\ln(y/\hat{\mu}) + (m-y)\ln((m-y)/(m-\hat{\mu}))]
Gamma	2\sum [-\ln(y/\hat{\mu}) + (y-\hat{\mu})/\hat{\mu}]
Inverse Gaussian	\sum (y-\hat{\mu})^2/(\hat{\mu}^2y)

Deviance as a Measure of Model Fit

The deviance can be used as a measure of fit of the model (“large values” indicate lack of fit).
We can use it to define a “\,\text{pseudo}~R^2\,”, as simply 1 - \frac{D(\boldsymbol{y},\widehat{\boldsymbol{\mu}})}{D_{\text{null}}}, where D_{\text{null}} is the deviance of the null model.
Warning 1: this should not be interpreted as a “proportion of variability in the reponse explained by the model”. Rather, it measures how close the log-likelihood of the model is to the log-likelihood of the saturated model.
Warning 2: it does not contain a penalty for adding parameters (hence, relying solely on this measure can lead to overfitting).
Warning 3: it can be close to 1 even if the choice of distribution for Y is “very wrong”.
Note: there are many other “pseudo R^2”, which you can read about on your favourite website.

Scaled Deviance: Asymptotic Result

Assuming the fitted model is correct, the scaled deviance approximately has a chi-squared distribution (asymptotically true) with degrees of freedom equal to the number of observations minus the number of estimated parameters: \frac{D(\boldsymbol{y},\widehat{\boldsymbol{\mu}})}{\psi} \to \chi^2_{n-(p+1)} \quad \text{when} \quad n\to\infty.

De Jong & Heller (2008) note that “[s]everal authors, for example (McCullagh and Nelder 1989, pp. 119, 122) caution against using the deviance as an overall goodness of fit measure in general”.
Instead, the scaled deviance is usually used to compare models that are nested (one model is a subset of another) by looking at the difference in their deviances (assessed against the quantiles of the chi-squared).

Model selection (Nested models)

Consider two models:
- Model 1 (q parameters): \eta=\beta_0+\beta_1x_1+\ldots\beta_qx_q
- Model 2 (p parameters): \eta=\beta_0+\beta_1x_1+\ldots\beta_qx_q+\beta_{q+1}x_{q+1}+\ldots\beta_px_p
We want to assess whether Model 2 is an improvement over the more parsimonious Model 1. That is, we want to test:

H_0: \beta_{q+1} = \cdots = \beta_p = 0 \quad \text{vs} \quad H_a: \text{at least one } \beta_j \text{ is non-zero}

Call D_1 and D_2 the scaled deviances of Model 1 (q parameters) and Model 2 (p parameters), respectively.
Model 2 is a significant improvement over Model 1, if D_1 - D_2 > \chi^2_{(p-q),1-\alpha}

Model selection (Nested models): Rule of Thumb

Rule of thumb: a critical value (at the 5% level) for a \chi^{2} distribution with \nu degrees of freedom is approximately 2\nu, i.e., \chi^2_{\nu, 95\%} \approx 2\nu \quad \iff \quad \mathbb{P} \left[ \chi^2(\nu)>2\nu \right] \approx 5\%
Note this overestimates the critical value for \nu \geq 8.
Using this rule of thumb, \text{model 2 is preferred if } D_{1}-D_{2} > 2(p-q).

Back to the Motor Claims Case Study

From our previous work on Avg.Claims, it looked like Cpol.Age was perhaps the “least useful” predictor in the model.
Let’s see if a model with “Car Group + Vehicule Age + Driver Age” improves on “Car Group + Vehicule Age”.
Warning: R gives you the “deviance”, not the “scaled deviance”.

Case Study: Null Model

#Null model
pcarins.glm.NULL <- glm(Avg.Claims~1, family=Gamma(link="log"), data = PCarIns)
pcarins.glm.NULL


Call:  glm(formula = Avg.Claims ~ 1, family = Gamma(link = "log"), data = PCarIns)

Coefficients:
(Intercept)  
      5.443  

Degrees of Freedom: 122 Total (i.e. Null);  122 Residual
Null Deviance:      27.84 
Residual Deviance: 27.84    AIC: 1486

Car Group + Vehicule Age

# Model with: Car Group + Vehicule Age
glm.car.vehage <- glm(Avg.Claims ~ Car.Group + Cveh.Age,
                   family=Gamma(link="log"),  data = PCarIns)
summary(glm.car.vehage)


Call:
glm(formula = Avg.Claims ~ Car.Group + Cveh.Age, family = Gamma(link = "log"), 
    data = PCarIns)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  5.52634    0.08340  66.264  < 2e-16 ***
Car.GroupB   0.06378    0.08886   0.718    0.474    
Car.GroupC   0.14365    0.08959   1.603    0.112    
Car.GroupD   0.48542    0.09216   5.267 6.46e-07 ***
Cveh.Age10+ -0.73371    0.09216  -7.962 1.28e-12 ***
Cveh.Age4-7 -0.10950    0.08886  -1.232    0.220    
Cveh.Age8-9 -0.43834    0.08959  -4.893 3.24e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Gamma family taken to be 0.1263283)

    Null deviance: 27.839  on 122  degrees of freedom
Residual deviance: 13.236  on 116  degrees of freedom
AIC: 1404.2

Number of Fisher Scoring iterations: 5

Car Group + Vehicule Age + Driver Age

# Model with: Age + Car + Vehicule Age (same model as earlier) 
glm.all <- glm(Avg.Claims ~ Car.Group + Cveh.Age + Cpol.Age,
                   family=Gamma(link="log"),  data = PCarIns)
summary(glm.all)


Call:
glm(formula = Avg.Claims ~ Car.Group + Cveh.Age + Cpol.Age, family = Gamma(link = "log"), 
    data = PCarIns)

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)    5.711672   0.103851  54.999  < 2e-16 ***
Car.GroupB     0.057942   0.075458   0.768  0.44422    
Car.GroupC     0.154767   0.076126   2.033  0.04448 *  
Car.GroupD     0.472303   0.078509   6.016 2.44e-08 ***
Cveh.Age10+   -0.735519   0.078509  -9.369 1.18e-15 ***
Cveh.Age4-7   -0.111420   0.075458  -1.477  0.14267    
Cveh.Age8-9   -0.422360   0.076126  -5.548 2.04e-07 ***
Cpol.Age21-24 -0.108184   0.114564  -0.944  0.34710    
Cpol.Age25-29  0.005219   0.113187   0.046  0.96331    
Cpol.Age30-34 -0.288110   0.113187  -2.545  0.01231 *  
Cpol.Age35-39 -0.331051   0.114564  -2.890  0.00465 ** 
Cpol.Age40-49 -0.280799   0.113187  -2.481  0.01464 *  
Cpol.Age50-59 -0.238162   0.113187  -2.104  0.03767 *  
Cpol.Age60+   -0.283549   0.113187  -2.505  0.01372 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for Gamma family taken to be 0.09110331)

    Null deviance: 27.839  on 122  degrees of freedom
Residual deviance: 11.265  on 109  degrees of freedom
AIC: 1398.1

Number of Fisher Scoring iterations: 7

Computing D_1-D_2

# Estimated dispersion (scale) parameter 
(psi <- summary(glm.all)$dispersion)

[1] 0.09110331

# Scaled deviances
(D1 <- glm.car.vehage$deviance/psi)

[1] 145.2905

(D2 <-  glm.all$deviance/psi)

[1] 123.6557

1-pchisq(D1-D2, df=7)

[1] 0.00293586

As the p-value is small, we should retain Cpol.Age in the model.
Note we reach the same conclusion with our rule of thumb, since D_1-D_2= 21.6348 is larger than 2 \cdot 7=14.

Case Study: using the anova() function instead

# analysis of the deviance table
print(anova(glm.all, test="Chi"))

Analysis of Deviance Table

Model: Gamma, link: log

Response: Avg.Claims

Terms added sequentially (first to last)

          Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                        122     27.839              
Car.Group  3   5.1916       119     22.648 2.587e-12 ***
Cveh.Age   3   9.4113       116     13.236 < 2.2e-16 ***
Cpol.Age   7   1.9710       109     11.265  0.002936 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Is adding interactions worth it?

glm.interactions <- glm(Avg.Claims ~ Car.Group + Cveh.Age + Cpol.Age 
                                      + Car.Group * Cveh.Age
                                      + Car.Group * Cpol.Age
                                      + Cveh.Age  * Cpol.Age, 
                        family=Gamma(link="log"),  data = PCarIns)
print(anova(glm.interactions, test="Chi"))

Analysis of Deviance Table

Model: Gamma, link: log

Response: Avg.Claims

Terms added sequentially (first to last)

                   Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                                 122    27.8394              
Car.Group           3   5.1916       119    22.6478 3.691e-12 ***
Cveh.Age            3   9.4113       116    13.2364 < 2.2e-16 ***
Cpol.Age            7   1.9710       109    11.2654  0.003272 ** 
Car.Group:Cveh.Age  9   0.3568       100    10.9086  0.919946    
Car.Group:Cpol.Age 21   1.9058        79     9.0028  0.480231    
Cveh.Age:Cpol.Age  21   2.6764        58     6.3264  0.113890    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model selection for Non-Nested models:

For non-nested model, we can still rely on the AIC (or BIC), \text{AIC} = 2d -2\ell(\boldsymbol{y}; \widehat{\boldsymbol{\mu}}) where d is the total number of parameters estimated.
Note AIC is automatically provided by R (recall that a smaller AIC is better).

Residuals in GLMs

In GLMs, residuals are still a primary tool for assessing how well a model fits the data.
They can help detect the form of the variance function and diagnose problematic observations.
The “response residuals” \, y_i - \widehat{\mu}_i\, are not especially useful, because they are not “supposed” to be well-behaved.
Deviance residuals are a common alternative: r_i^D = \text{sign}(y_i - \widehat{\mu}_i) \sqrt{d_i}, where d_{i} is the contribution of the ith observation to the scaled deviance (drawing on the idea that deviance is akin to RSS).

Residuals in GLMs (continued)

If the model is correct and the sample size n is large, then the (scaled) deviance is approximately \chi^2_{n-(p+1)}.
The expected value of the deviance is thus n-(p+1), and one expects each case to contribute approximately (n-(p+1))/n\approx 1 to the deviance.
If |d_i| is much greater than 1, then case i is contributing too much to the deviance (contributing to lack of fit), indicating a departure from the model assumptions for that case.
Typically deviance residuals are examined by plotting them against fitted values or explanatory variables.
Another common alternative is the Pearson residuals: r_i^P = \dfrac{y_i - \widehat{\mu}_i}{\sqrt{V(\widehat{\mu}_i)}}.

Case Study: Motor claims illustration - Residual

plot(pcarins.glm, which = 1:2)

Case Study: Motor claims illustration - Residual

plot(pcarins.glm, which = c(3,5))

References

De Jong, P., & Heller, G. Z. (2008). Generalized linear models for insurance data. Cambridge University Press.

Haberman, S., & Renshaw, A. E. (1996). Generalized linear models and actuarial science. Journal of the Royal Statistical Society: Series D (The Statistician), 45(4), 407–436.

McCullagh, P., & Nelder, J. A. (1989). Generalized linear models (2nd ed.). Routledge.