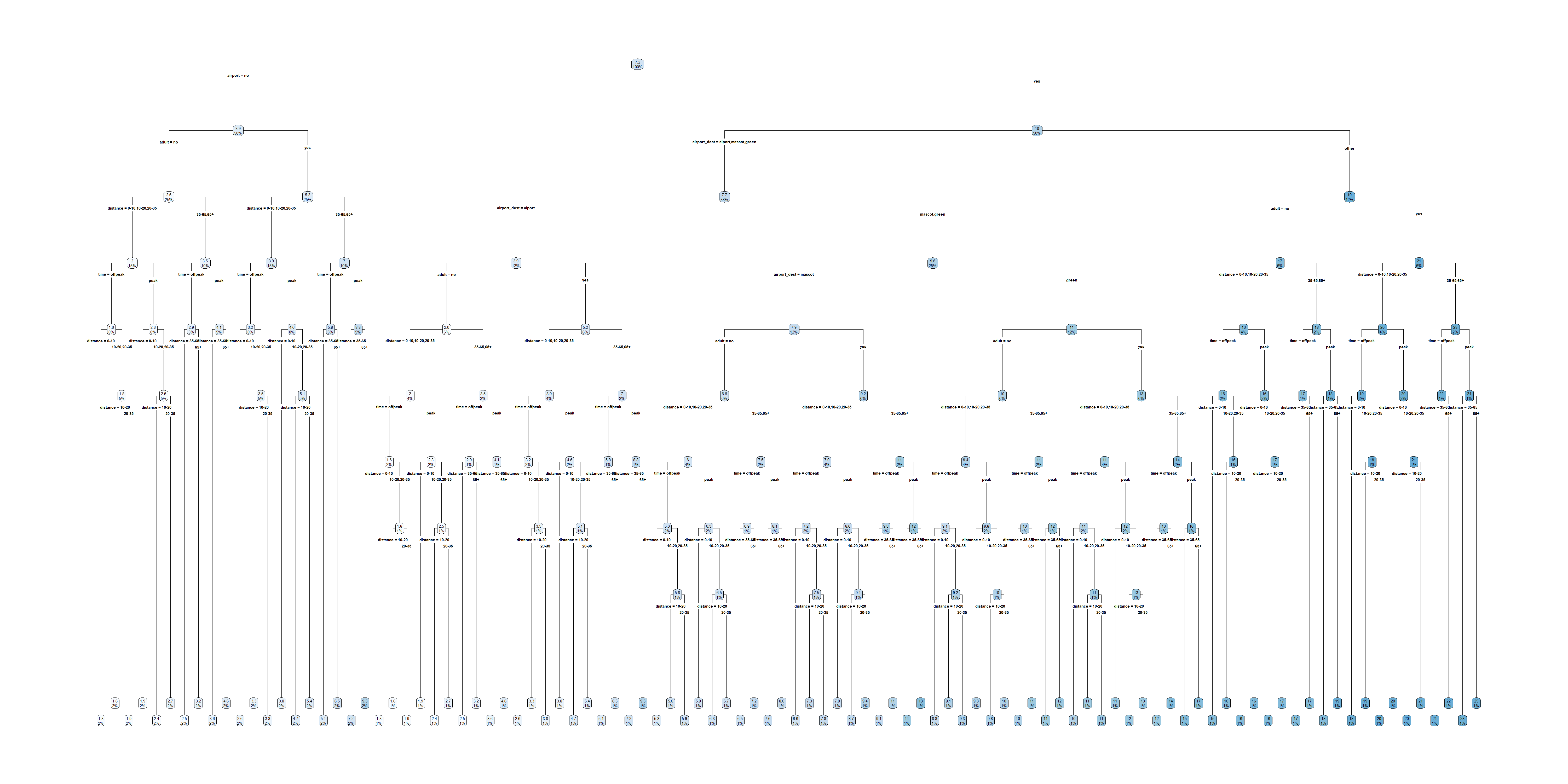
graph TB
A{Is it peak hour?}
A-->|Yes| B[Peak Hour]
A-->|No| C[Off-Peak Hour]
B--> D{Distance?}
D-->|0 - 10 km| E[$3.79]
D-->|10 - 20 km| F[$4.71]
D-->|20 - 35 km| G[$5.42]
D-->|35 - 65 km| H[$7.24]
D-->|65+ km| I[$9.31]
C--> J{Distance?}
J-->|0 - 10 km| K[$2.65]
J-->|10 - 20 km| L[$3.29]
J-->|20 - 35 km| M[$3.79]
J-->|35 - 65 km| N[$5.06]
J-->|65+ km| O[$6.51]
Tree-Based Methods
ACTL3142 & ACTL5110 Statistical Machine Learning for Risk Applications
Overview
- Decision Trees
- Growing a Tree
- National Flood Insurance Program Demo
- Pruning a Tree
- Bootstrap Aggregation
- Random Forests
- Boosting
Summary
Decision trees
- Stratify / segment the predictor space into a number of simple regions.
- The set of splitting rules can be summarised in a tree.
Bagging, random forests, boosting
- Examples of what we call “ensemble methods”.
- Produce multiple trees.
- Improve the prediction accuracy of tree-based methods.
- Lose some interpretation.
Decision Trees
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
Trees in a nutshell
Decision trees are a simple, easy to interpret, and popular method for both regression and classification tasks. They can be used to make predictions, but also simply as “data exploration” to understand a data set better.
They make predictions by partitioning the predictor space into a number of simple regions, and making a constant prediction within each region. The set of splitting rules can be summarised in a tree. “Stand alone” tree models are rarely particularly accurate, but they form the basis for more accurate (and complex) methods like random forests and boosting.

How much is a train ticket?
In code
rail_cost <- function(peak_hours, distance) {
if (peak_hours) {
if (distance <= 10) {
cost <- 3.79
} else if (distance <= 20) {
cost <- 4.71
} else if (distance <= 35) {
cost <- 5.42
} else if (distance <= 65) {
cost <- 7.24
} else {
cost <- 9.31
}
} else {
if (distance <= 10) {
cost <- 2.65
} else if (distance <= 20) {
cost <- 3.29
} else if (distance <= 35) {
cost <- 3.79
} else if (distance <= 65) {
cost <- 5.06
} else {
cost <- 6.51
}
}
return(cost)
}def rail_cost(peak_hours, distance):
if peak_hours:
if distance <= 10:
cost = 3.79
elif distance <= 20:
cost = 4.71
elif distance <= 35:
cost = 5.42
elif distance <= 65:
cost = 7.24
else:
cost = 9.31
else:
if distance <= 10:
cost = 2.65
elif distance <= 20:
cost = 3.29
elif distance <= 35:
cost = 3.79
elif distance <= 65:
cost = 5.06
else:
cost = 6.51
return costHitters dataset
Unnamed: 0 AtBat Hits HmRun ... Assists Errors Salary NewLeague
0 -Alan Ashby 315 81 7 ... 43 10 475.0 N
1 -Alvin Davis 479 130 18 ... 82 14 480.0 A
2 -Andre Dawson 496 141 20 ... 11 3 500.0 N
3 -Andres Galarraga 321 87 10 ... 40 4 91.5 N
4 -Alfredo Griffin 594 169 4 ... 421 25 750.0 A
.. ... ... ... ... ... ... ... ... ...
258 -Willie McGee 497 127 7 ... 9 3 700.0 N
259 -Willie Randolph 492 136 5 ... 381 20 875.0 A
260 -Wayne Tolleson 475 126 3 ... 113 7 385.0 A
261 -Willie Upshaw 573 144 9 ... 131 12 960.0 A
262 -Willie Wilson 631 170 9 ... 4 3 1000.0 A
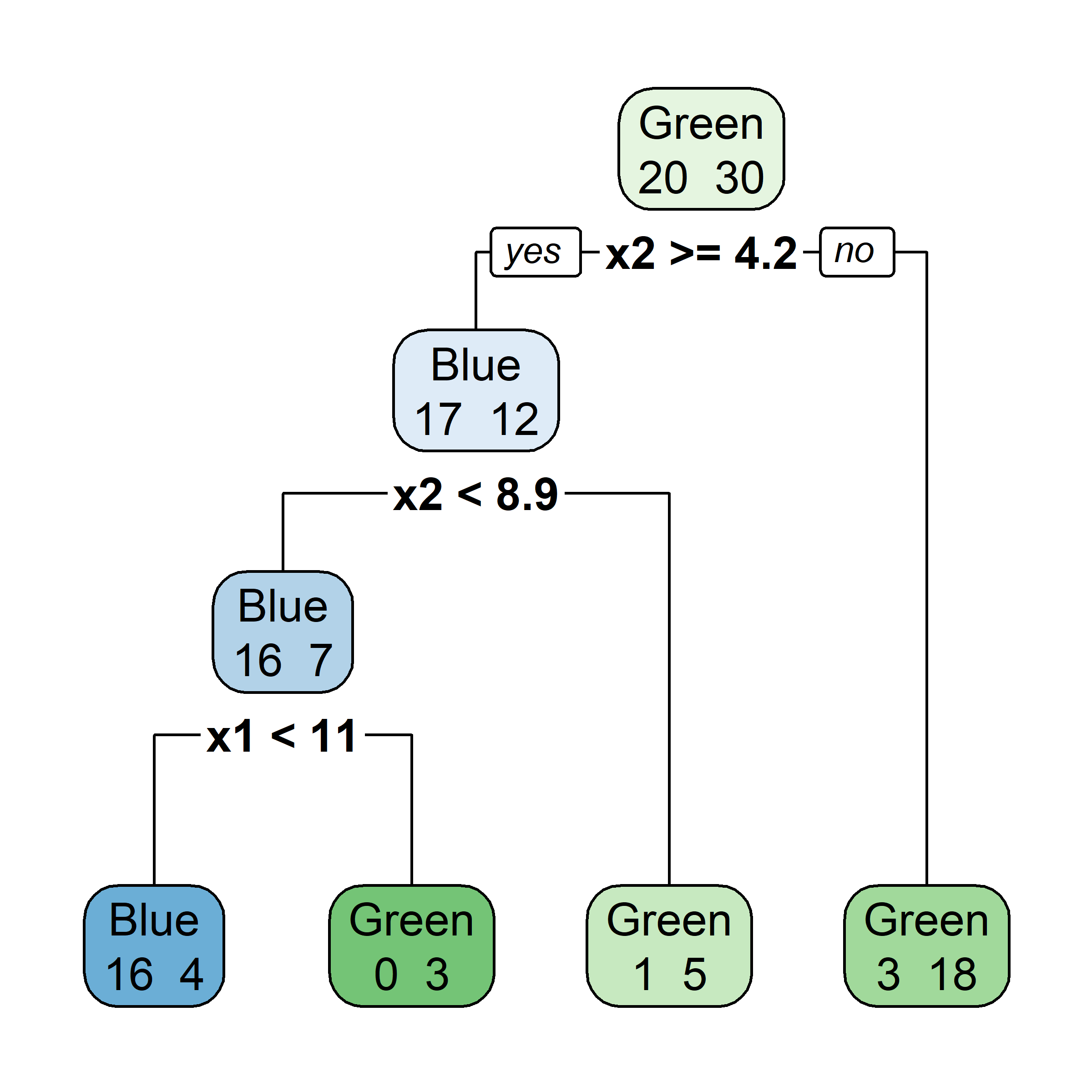
[263 rows x 21 columns]Fit a basic tree
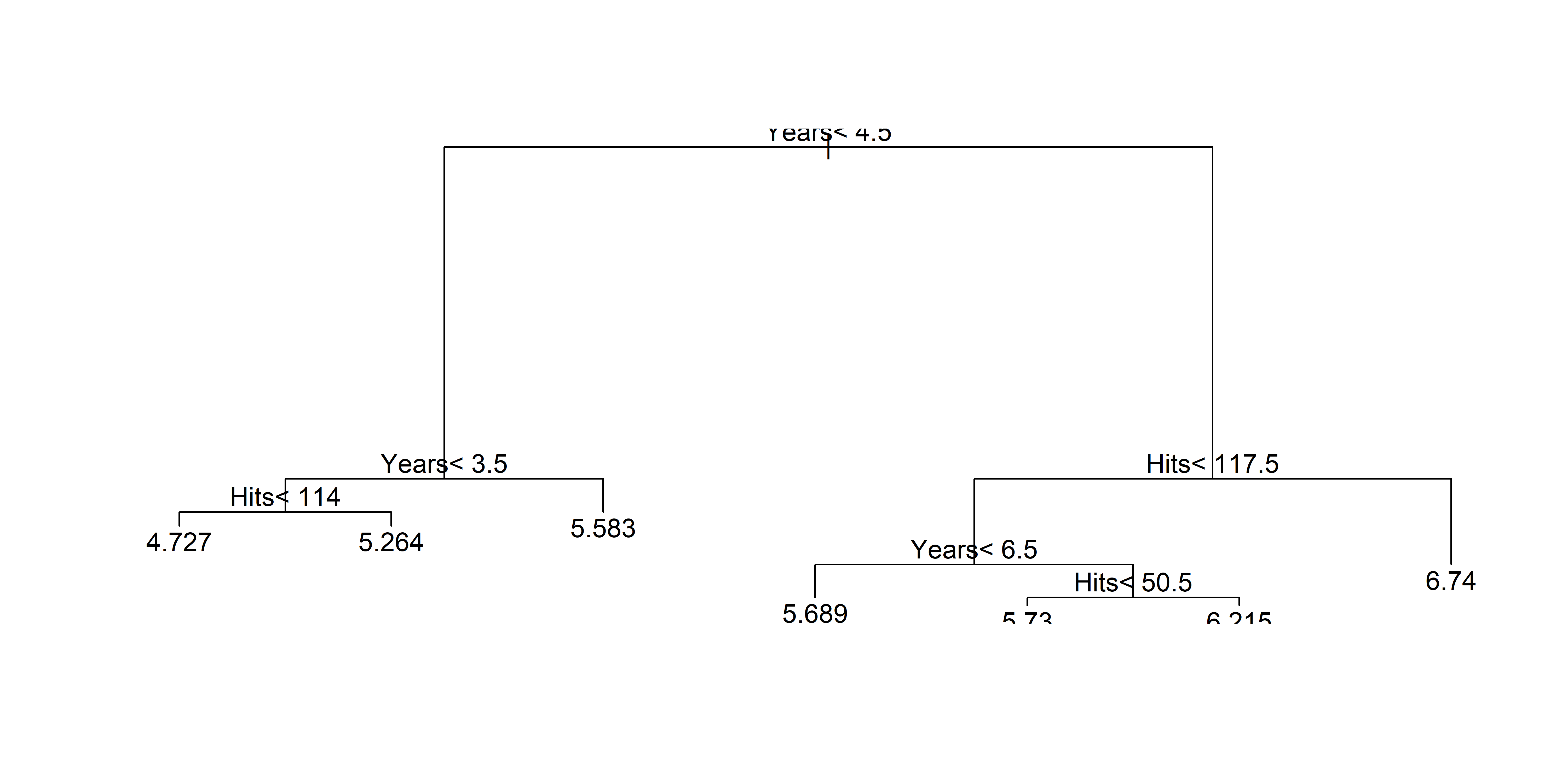
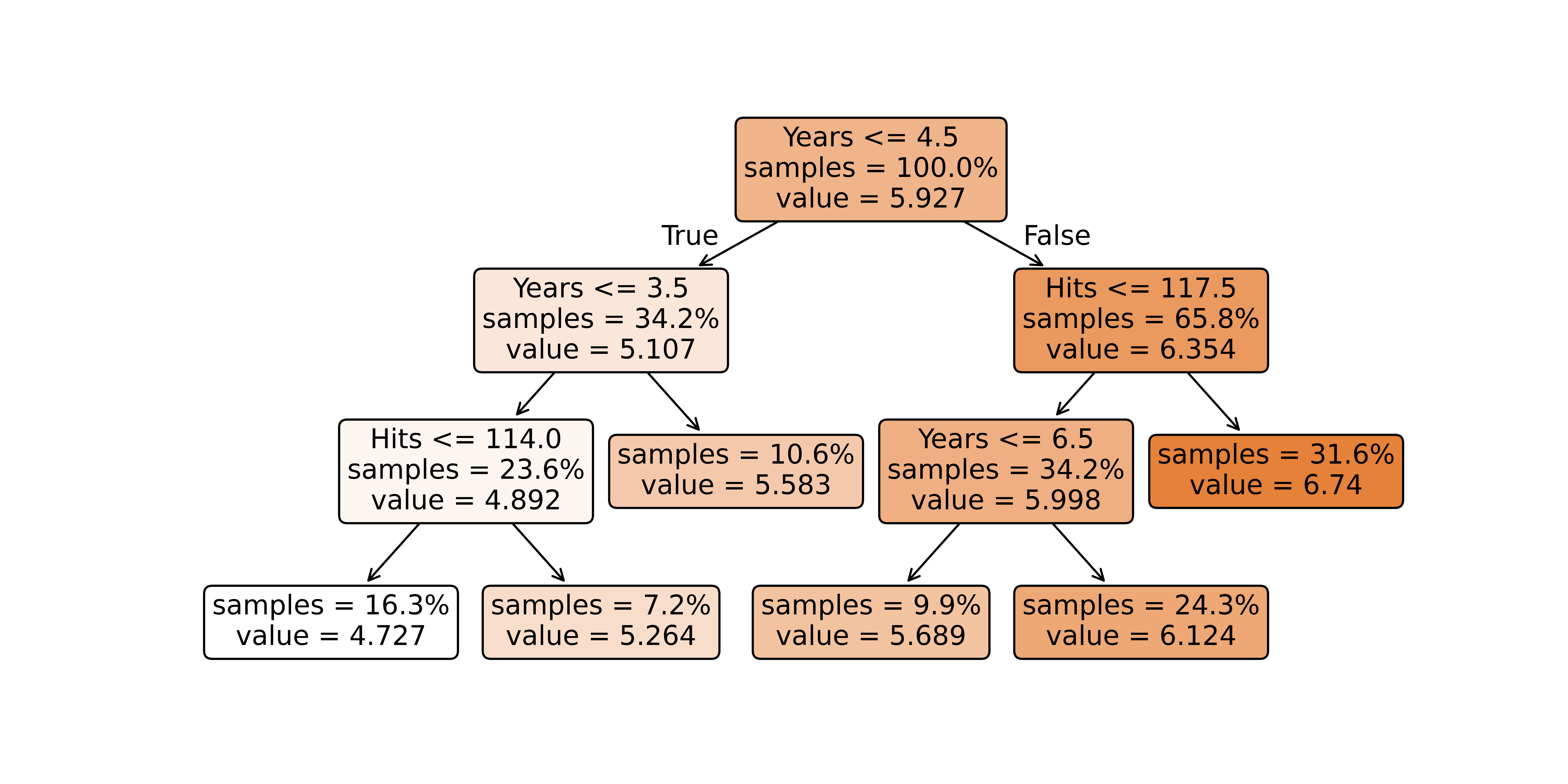
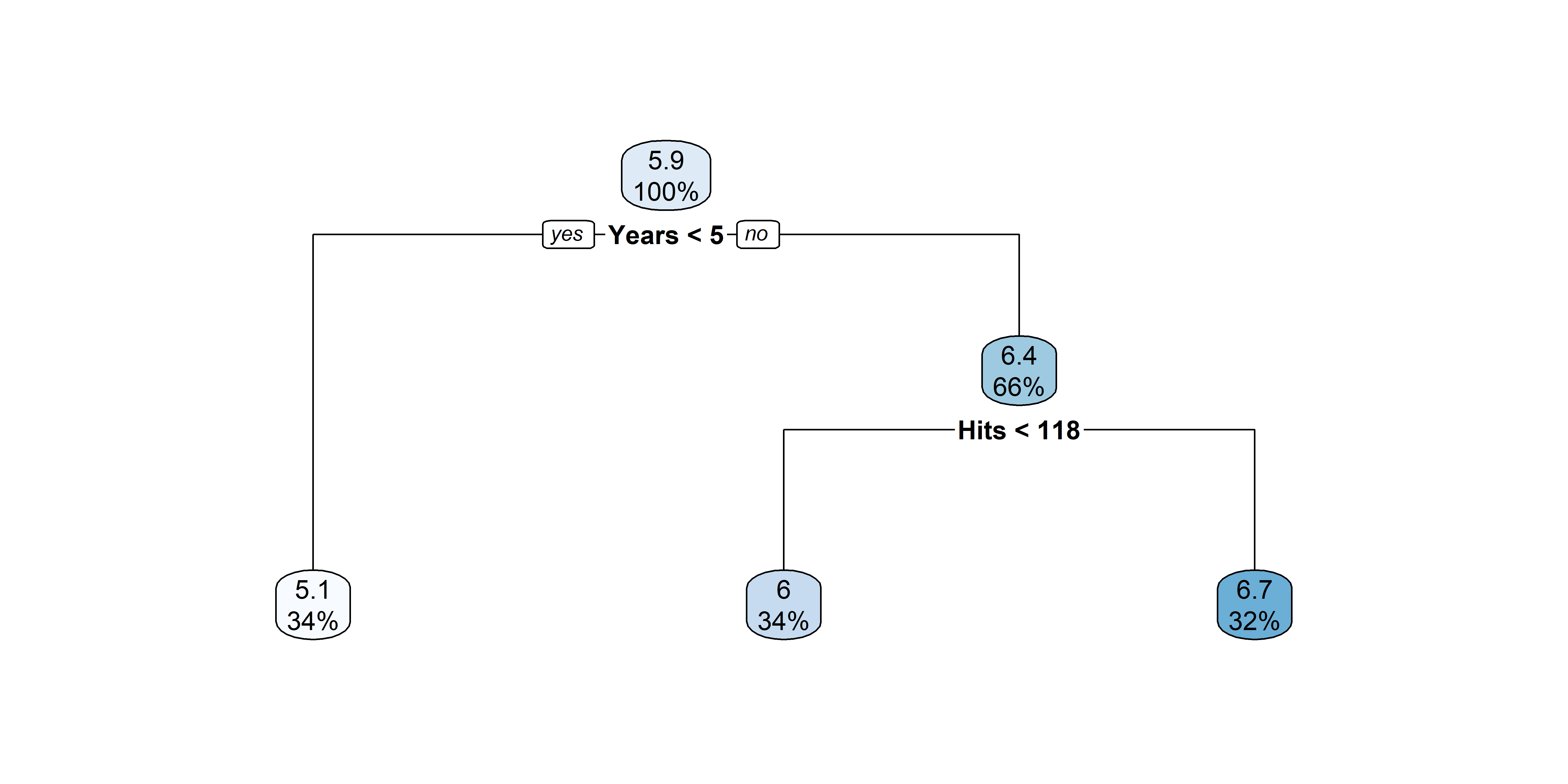
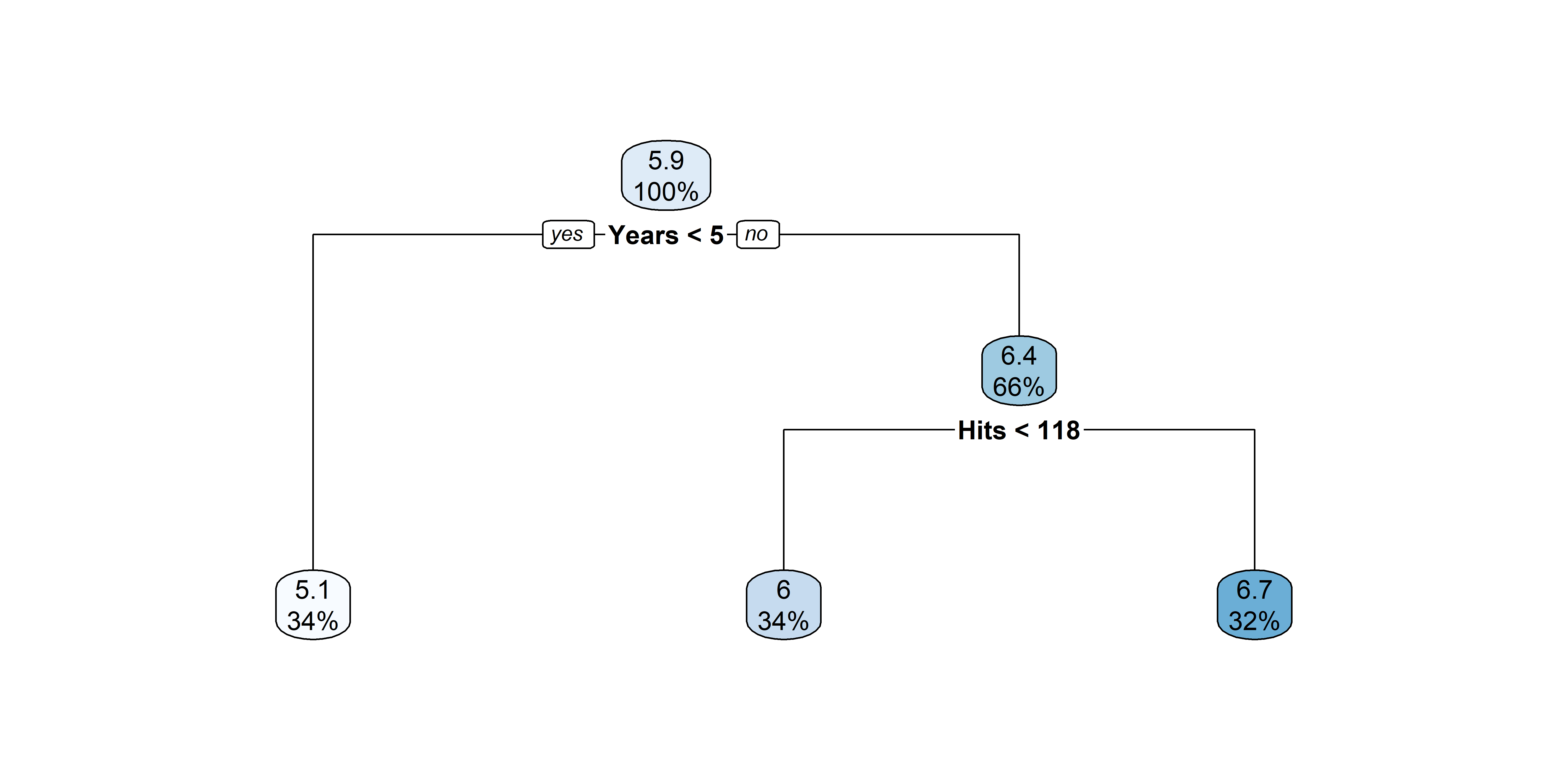
n= 263
node), split, n, deviance, yval
* denotes terminal node
1) root 263 207.153700 5.927222
2) Years< 4.5 90 42.353170 5.106790
4) Years< 3.5 62 23.008670 4.891812
8) Hits< 114 43 17.145680 4.727386 *
9) Hits>=114 19 2.069451 5.263932 *
5) Years>=3.5 28 10.134390 5.582812 *
3) Years>=4.5 173 72.705310 6.354036
6) Hits< 117.5 90 28.093710 5.998380
12) Years< 6.5 26 7.237690 5.688925 *
13) Years>=6.5 64 17.354710 6.124096
26) Hits< 50.5 12 2.689439 5.730017 *
27) Hits>=50.5 52 12.371640 6.215037 *
7) Hits>=117.5 83 20.883070 6.739687 *X = hitters[['Years', 'Hits']]
y = np.log(hitters['Salary'])
tree = DecisionTreeRegressor(min_samples_split=20, min_samples_leaf=10, max_depth=3, ccp_alpha=0.01)
tree.fit(X, y);
print(export_text(tree, feature_names=['Years', 'Hits']))|--- Years <= 4.50
| |--- Years <= 3.50
| | |--- Hits <= 114.00
| | | |--- value: [4.73]
| | |--- Hits > 114.00
| | | |--- value: [5.26]
| |--- Years > 3.50
| | |--- value: [5.58]
|--- Years > 4.50
| |--- Hits <= 117.50
| | |--- Years <= 6.50
| | | |--- value: [5.69]
| | |--- Years > 6.50
| | | |--- value: [6.12]
| |--- Hits > 117.50
| | |--- value: [6.74]Source: These plots are recreating ISLR2’s Figure 8.4.
Nicer plots for decision trees
After pruning that tree
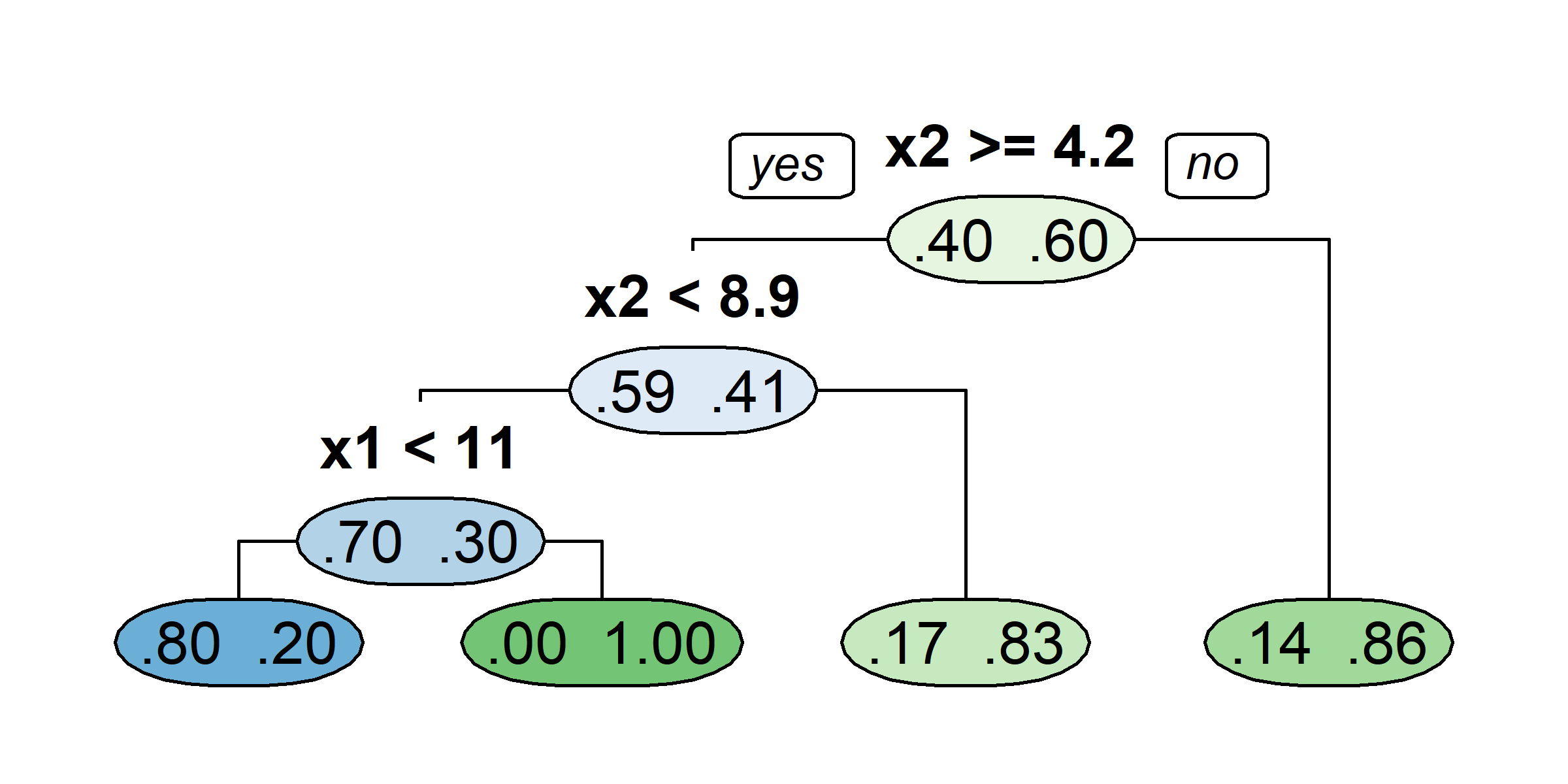
Source: A recreation of ISLR2’s Figure 8.1.
Tree Terminology
Regions in the predictor space
Code
ggplot(Hitters, aes(x = Years, y = Hits, colour = log(Salary))) +
geom_point() +
geom_vline(xintercept = 4.5, colour = "black", linetype = "dashed") +
annotate("segment", x = 4.5, xend = 24, y = 117.5, yend = 117.5, colour = "black", linetype = "dashed") +
annotate("text", x = 2, y = 200, label = "R[1]", parse = TRUE, size = 10) +
annotate("text", x = 20, y = 50, label = "R[2]", parse = TRUE, size = 10) +
annotate("text", x = 20, y = 200, label = "R[3]", parse = TRUE, size = 10) +
theme(text = element_text(size = 20))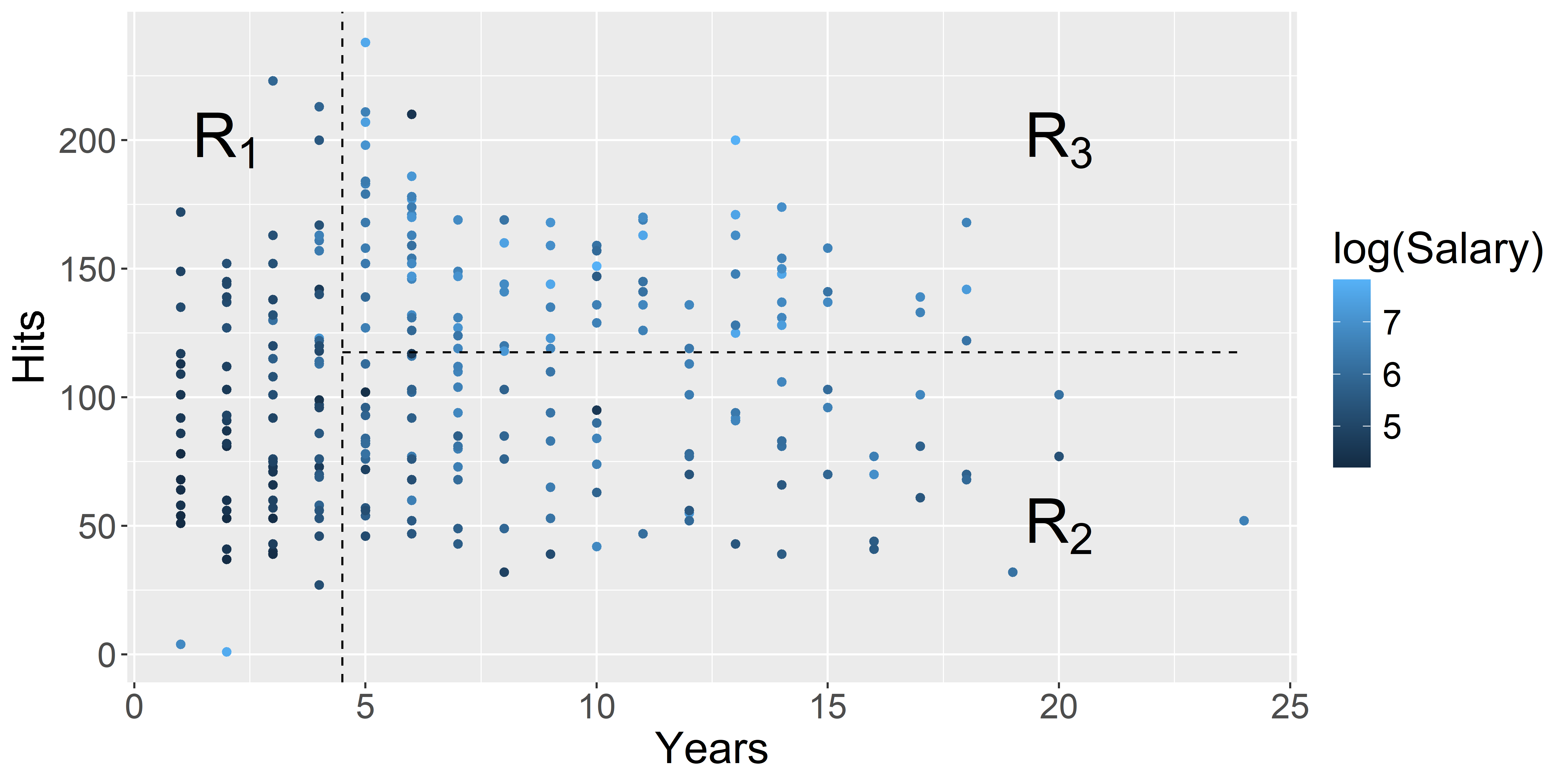
Source: A recreation of ISLR2’s Figure 8.2.
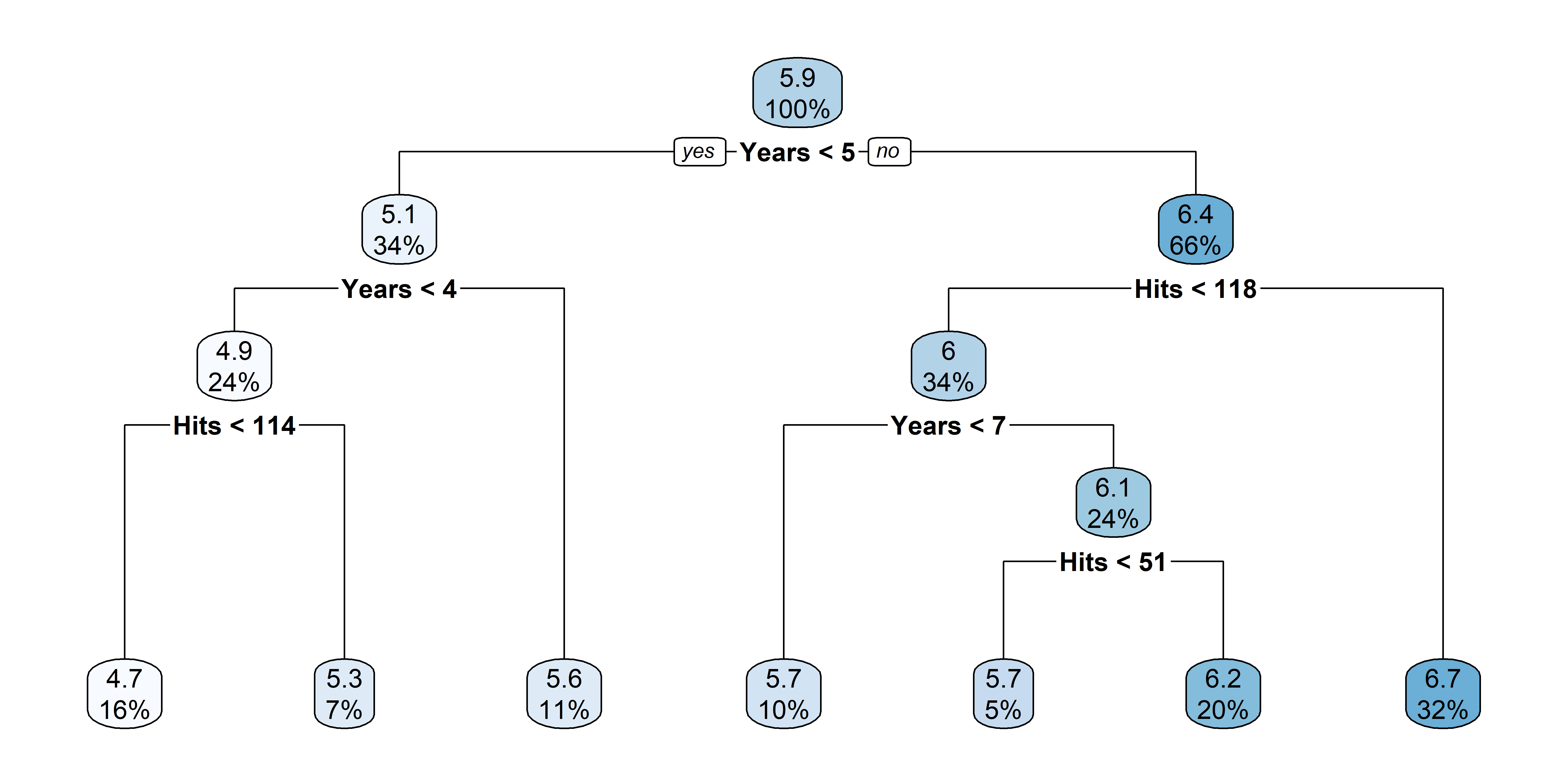
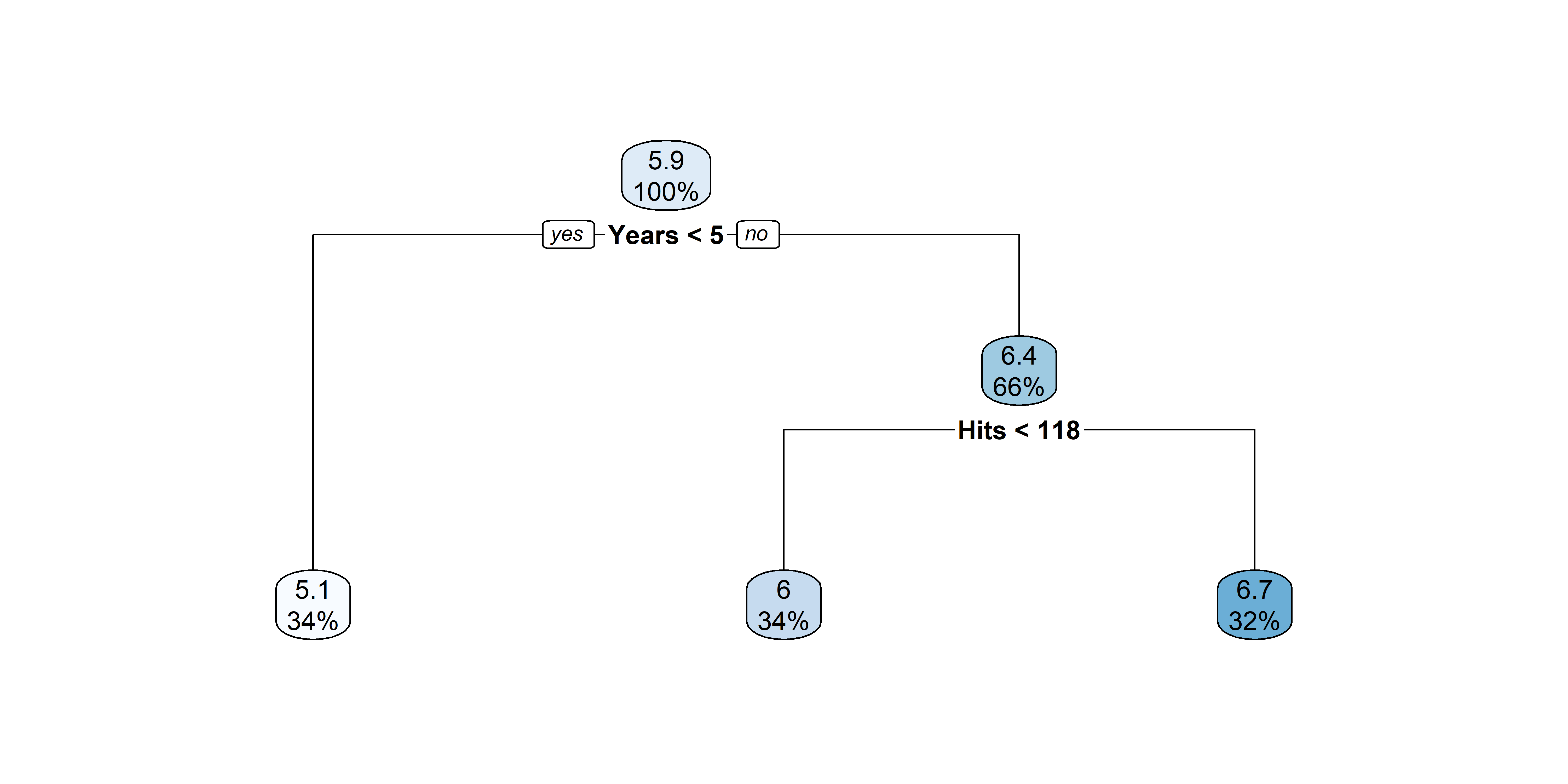
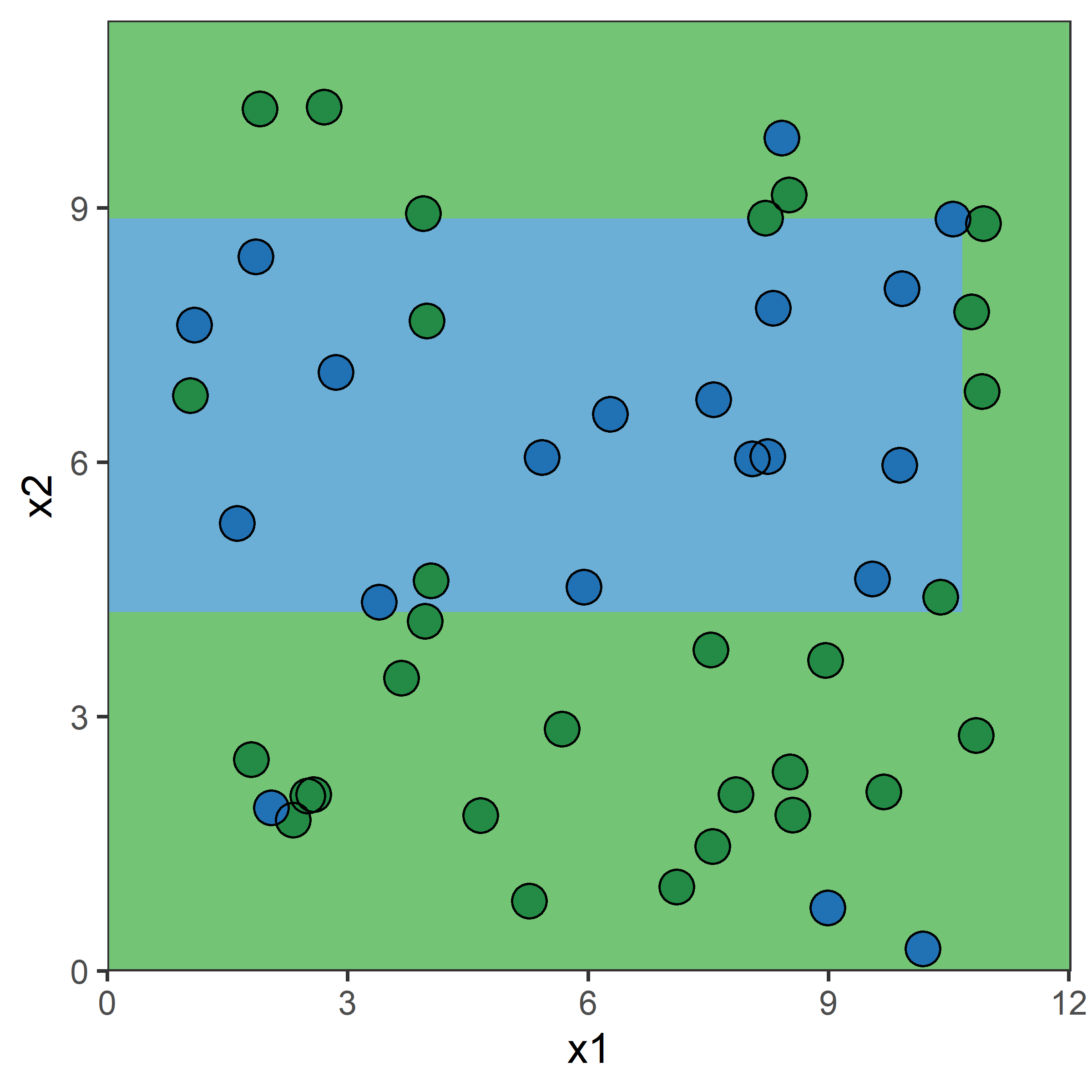
Tree regions & predictions
A decision tree is made by:
- Dividing the predictor space (i.e. the set of possible values for X_1, X_2, \dots, X_p) into J distinct and non-overlapping regions, R_1, R_2, \dots, R_J,
- Making the same prediction for every observation that falls into the region R_j
- the mean response for the training data in R_j (regression trees)
- the mode response for the training data in R_j (classification trees)
Hitters example:
| Region | Predicted salaries |
|---|---|
| R_1 = \{X | \mathtt{Years} < 4.5 \} | \$1,000 \times \mathrm{e}^{5.107} = \$165,174 |
| R_2 = \{X | \mathtt{Years} \geq 4.5, \mathtt{Hits} < 117.5 \} | \$1,000 \times \mathrm{e}^{5.999} = \$402,834 |
| R_3 = \{X | \mathtt{Years} \geq 4.5, \mathtt{Hits} \geq 117.5 \} | \$1,000 \times \mathrm{e}^{6.740} = \$845,346 |
Discussion
Decision trees: summary
- Decision trees are simple, popular, and easy to interpret.
- They are not the most accurate method, but they can be great to understand the data.
- They do form the basis for more accurate and complex methods like random forests and boosting.
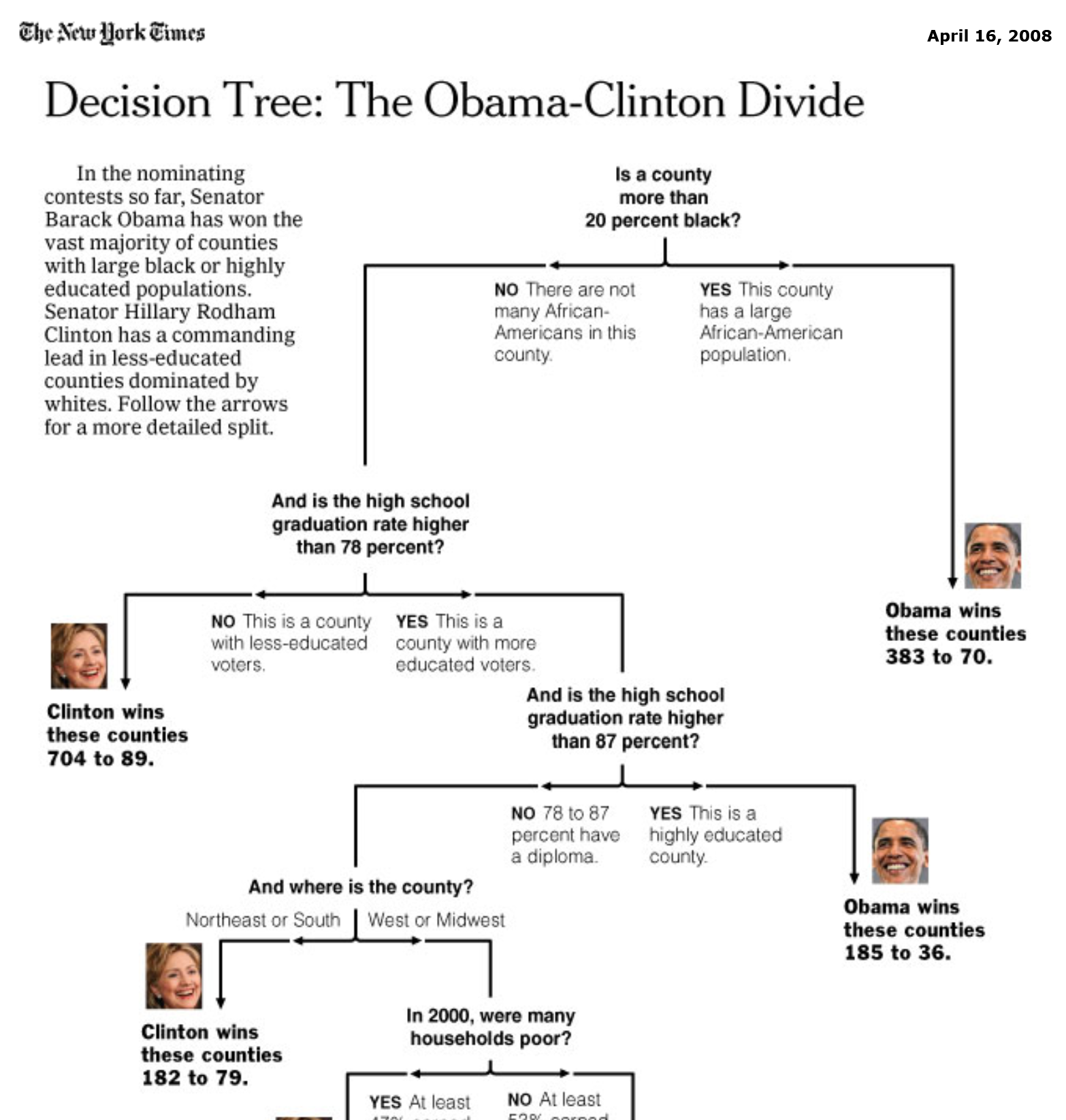
Source: New York Times (2008), Decision Tree: The Obama-Clinton Divide.
Non-binary train cost tree
A decision tree enforces binary splits…
graph TB
A{Peak hour?}
A-->|Yes| B[Peak Hour]
A-->|No| C[Off-Peak Hour]
B--> D{Distance?}
D-->|0 - 10 km| E[$3.79]
D-->|10 - 20 km| F[$4.71]
D-->|20 - 35 km| G[$5.42]
D-->|35 - 65 km| H[$7.24]
D-->|65+ km| I[$9.31]
C--> J{Distance?}
J-->|0 - 10 km| K[$2.65]
J-->|10 - 20 km| L[$3.29]
J-->|20 - 35 km| M[$3.79]
J-->|35 - 65 km| N[$5.06]
J-->|65+ km| O[$6.51]
Binary train cost tree
… but we can still represent non-binary splits in a binary tree.
graph TB
A{Peak hour?}
A-->|Yes| B[Peak Hour]
A-->|No| J[Off-Peak Hour]
B--> D1[0 - 10 km: $3.79]
B--> D2[10 km +]
D2--> F1[10 - 20 km: $4.71]
D2--> G1[20 km +]
G1--> H1[20 - 35 km: $5.42]
G1--> I1[35 km +]
I1--> I2[35 - 65 km: $7.24]
I1--> I3[65 km +: $9.31]
J--> K1[0 - 10 km: $2.65]
J--> L1[10 km +]
L1--> L2[10 - 20 km: $3.29]
L1--> M1[20 km +]
M1--> M2[20 - 35 km: $3.79]
M1--> N1[35 km +]
N1--> N2[35 - 65 km: $5.06]
N1--> O[65 km +: $6.51]
Popular (IME 2023 abstracts)
Random Forests for Wildfire Insurance Applications: Mélina Mailhot, Concordia University
Homeowners’ insurance in wildfire-prone areas can be a very risky business that some insurers may not be willing to undertake. We create an actuarial spatial model for the likelihood of wildfire occurrence over a fine grid map of North America. Several models are used, such as generalized linear models and tree-based machine learning algorithms. A detailed analysis and comparison of the models show a best fit using random forests. Sensitivity tests help in assessing the effect of future changes in the covariates of the model. A downscaling exercise is performed, focusing on some high-risk states and provinces. The model provides the foundation for actuaries to price, reserve, and manage the financial risk from severe wildfires.
A Machine Learning Approach to Forecasting Italian Honey Production with Tree-Based Methods: Elia Smaniotto, University of Florence
The Italian apiculture sector, one of the largest honey producers in Europe, has suffered considerable damage in recent years. Adverse weather conditions, occurring more frequently as climate change progresses, can be high-impact and cause the environment to be unfavourable to the bees’ activity [1]. In this paper, we aim to study the effect of climatic and meteorological events on honey production. The database covers several hives, mainly located in northern Italy, and contains temperature, precipitations, geographical and meteorological measurements. We adopt random forest and gradient boosting algorithms, powerful and flexible tree-based methods to predict the honey production variation. Then, a feature importance analysis is performed to discover the main driver of honey production within the covered area. This study, which lies within the existing literature [2,3], seeks to establish the links between weather conditions and honey production, aiming to protect bees’ activity better and assess potential losses for beekeepers.
Improving Business Insurance Loss Models by Leveraging InsurTech Innovation, Emiliano Valdez, University of Connecticut
Recent transformative and disruptive developments in the insurance industry embrace various InsurTech innovations. In particular, with the rapid advances in data science and computational infrastructure, InsurTech is able to incorporate multiple emerging sources of data and reveal implications for value creation on business insurance by enhancing current insurance operations. In this paper, we unprecedentedly combine real-life proprietary insurance claims information and its InsurTech empowered risk factors describing insured businesses to create enhanced tree-based loss models. An empirical study in this paper shows that the supplemental data sources created by InsurTech innovation significantly help improve the underlying insurance company’s internal or inhouse pricing models. The results of our work demonstrate how InsurTech proliferates firm-level value creation and how it can affect insurance product development, pricing, underwriting, claim management, and administration practice.
On the Pricing of Capped Volatility Swaps using Machine Learning Techniques, Eva Verschueren, KU Leuven
A capped volatility swap is a forward contract on an asset’s capped, annualized realized volatility, over a predetermined period of time. The volatility swap allows investors to get a pure exposure to the volatility of the underlying asset, making the product an interesting instrument for both hedging and speculative purposes. In this presentation, we develop data-driven machine learning techniques in the context of pricing capped volatility swaps. To this purpose, we construct unique data sets comprising both the delivery price of contracts at initiation and the daily observed prices of running contracts. In order to predict future realized volatility, we explore distributional information on the underlying asset, specifically by extracting information from the forward implied volatilities and market-implied moments of the asset. The pricing performance of tree-based machine learning models and a Gaussian process regression model is presented in a tailored validation setting.
Integrated Design for Index Insurance, Jinggong Zhang, Nanyang Technological University
Weather index insurance (WII) is a promising tool for agricultural risk mitigation, but its popularity is often hindered by challenges of product design, such as basis risk, weather index selection and product complexity issues. In this paper we develop machine learning methodologies to design the statistically optimal WII to address those critical concerns in the literature and practice. The idea from tree-based models is exploited to simultaneously achieve weather variable selection and payout function determination, leading to effective basis risk reduction. The proposed framework is applied to an empirical study where high-dimensional weather variables are adopted to hedge soybean production losses in Iowa. Our numerical results show that the designed insurance policies are potentially viable with much lower government subsidy, and therefore can enhance social welfare.
Bayesian CART for insurance pricing, Yaojun Zhang, University of Leeds
An insurance portfolio offers protection against a specified type of risk to a collection of policyholders with various risk profiles. Insurance companies use risk factors to group policyholders with similar risk profiles in tariff classes. Premiums are set to be equal for policyholders within the same tariff class which should reflect the inherent riskiness of each class. Tree-based methods, like the classification and regression tree (CART), have gained popularity as they can in some cases give good performance and be easily interpretable. In this talk, we discuss a Bayesian approach applied to CART models. The idea is to have the prior induce a posterior distribution that will guide the stochastic search using MCMC towards more promising trees. We shall introduce different Bayesian CART models for the insurance claims data, which include the frequency-severity model and the (zero-inflated) compound Poisson model. Some simulation and real data examples will be discussed.
Machine Learning in Long-term Mortality Forecasting, Wenjun Zhu, Nanyang Technological University
We propose a new machine learning-based framework for long-term mortality forecasting. Based on ideas of neighbouring prediction, model ensembling, and tree boosting, this framework can significantly improve the prediction accuracy of long-term mortality. In addition, the proposed framework addresses the challenge of a shrinking pattern in long-term forecasting with information from neighbouring ages and cohorts. An extensive empirical analysis is conducted using various countries and regions in the Human Mortality Database. Results show that this framework reduces the mean absolute percentage error (MAPE) of the 20-year forecasting by almost 50% compared to classic stochastic mortality models, and it also outperforms deep learning-based benchmarks. Moreover, including mortality data from multiple populations can further enhance the long-term prediction performance of this framework.
Growing a Tree
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
Fitting a regression tree
- Divide the predictor space into high-dimensional rectangles, or boxes.
- The goal is to find boxes R_1, R_2, \ldots, R_J that minimise \mathrm{RSS} = \sum_{j=1}^{J} \sum_{i \in R_j} (y_i - \hat{y}_{R_j})^2 where \hat{y}_{R_j} is the mean response for the training observations within the jth box.
- It is computationally unfeasible to consider every possible partition.
- So, we take stepwise greedy approach: at each step, we pick the split that most reduces the error “right now”.
- As in linear regression “forward stepwise selection”, nothing guarantees this yields the “optimal” splits, overall.
Illustraion with a synthetic regression dataset
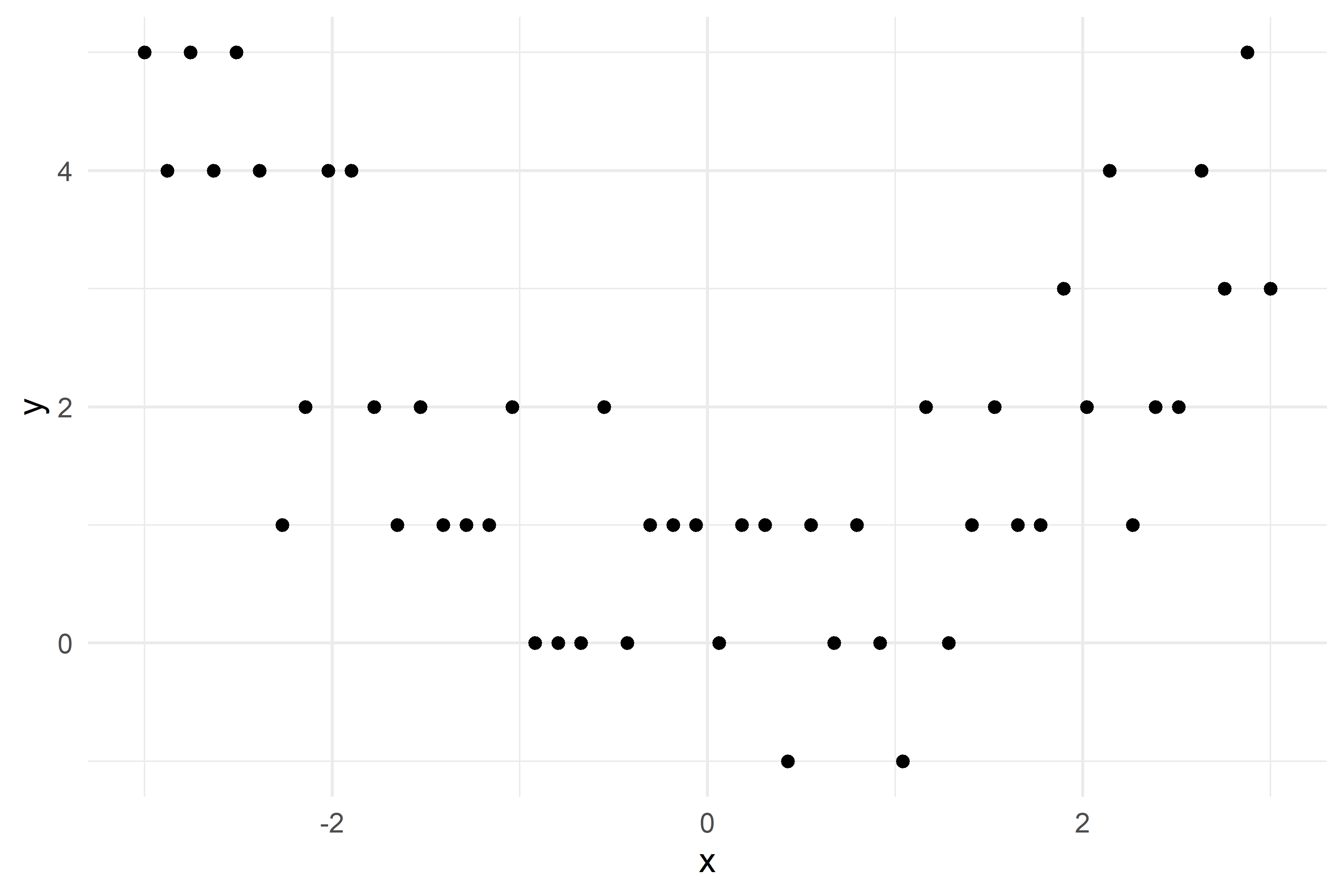
Growing a regression tree I
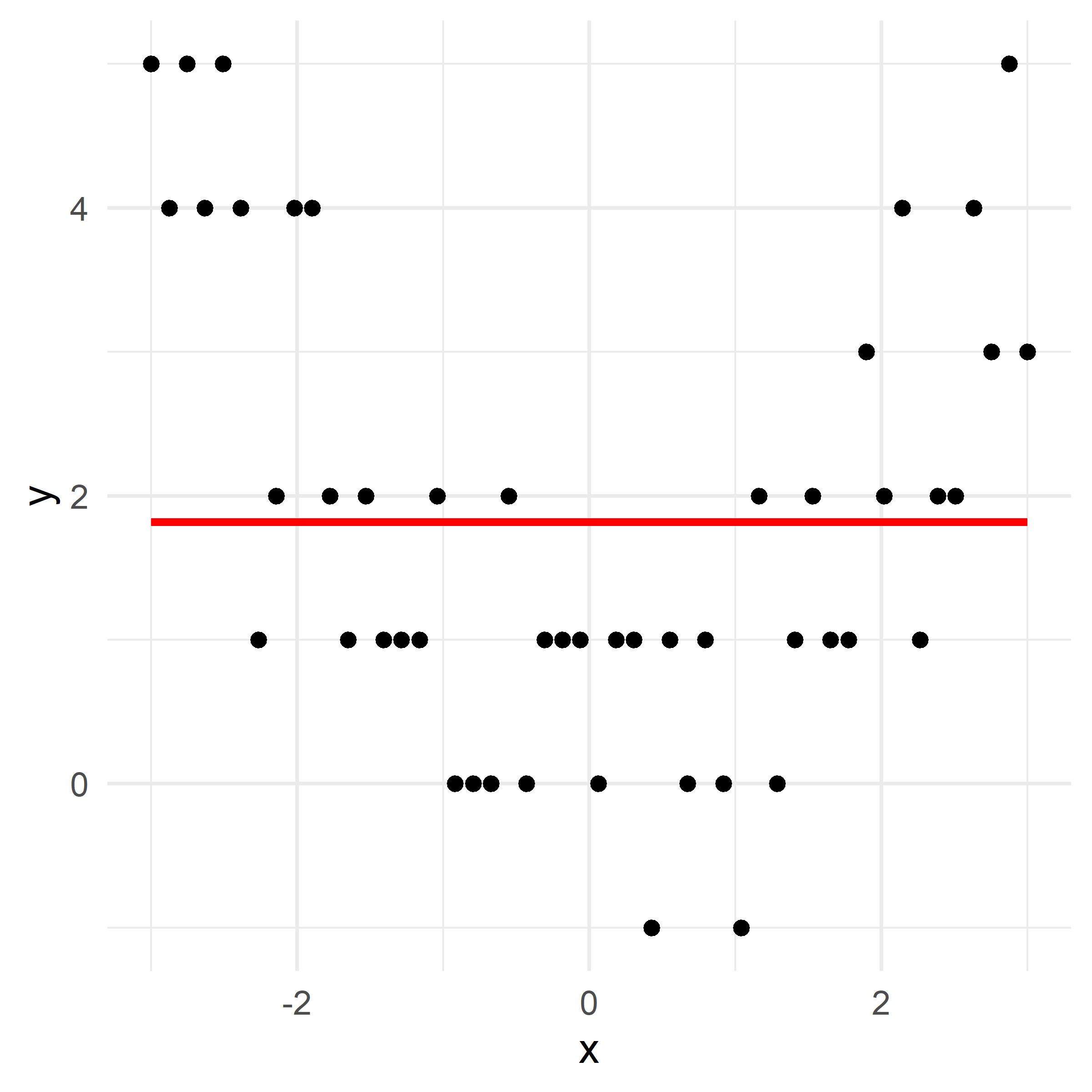
Growing a regression tree II
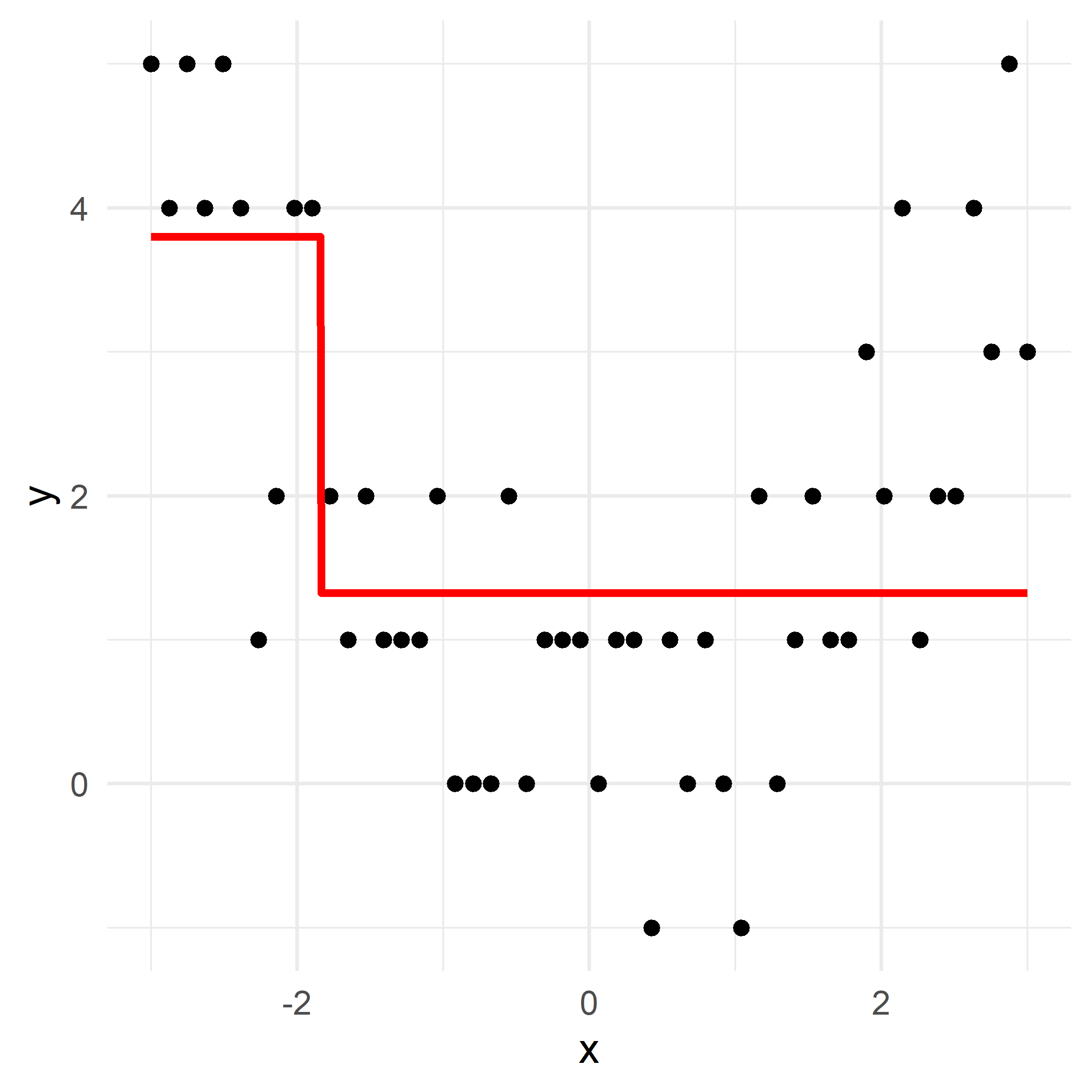
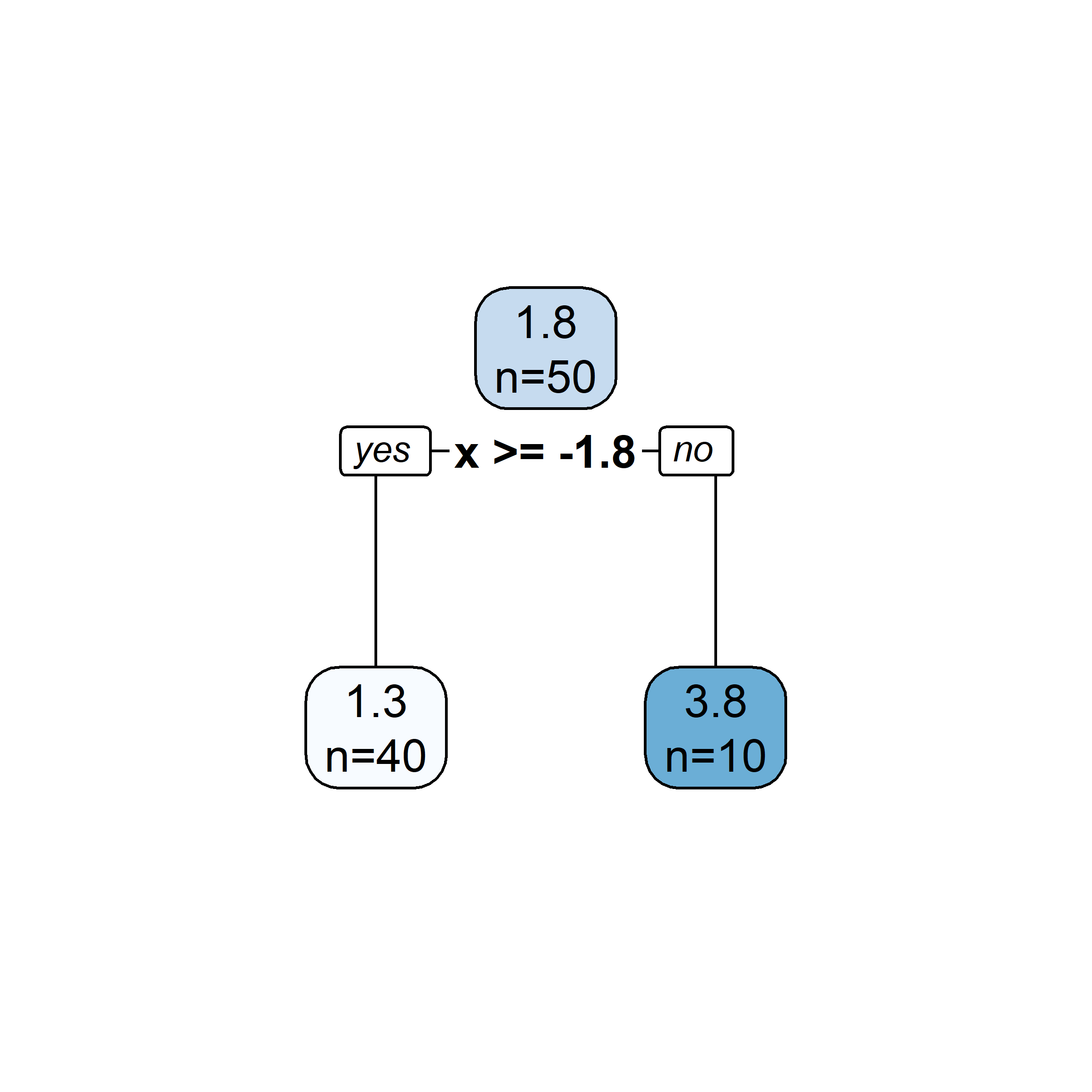
Growing a regression tree III
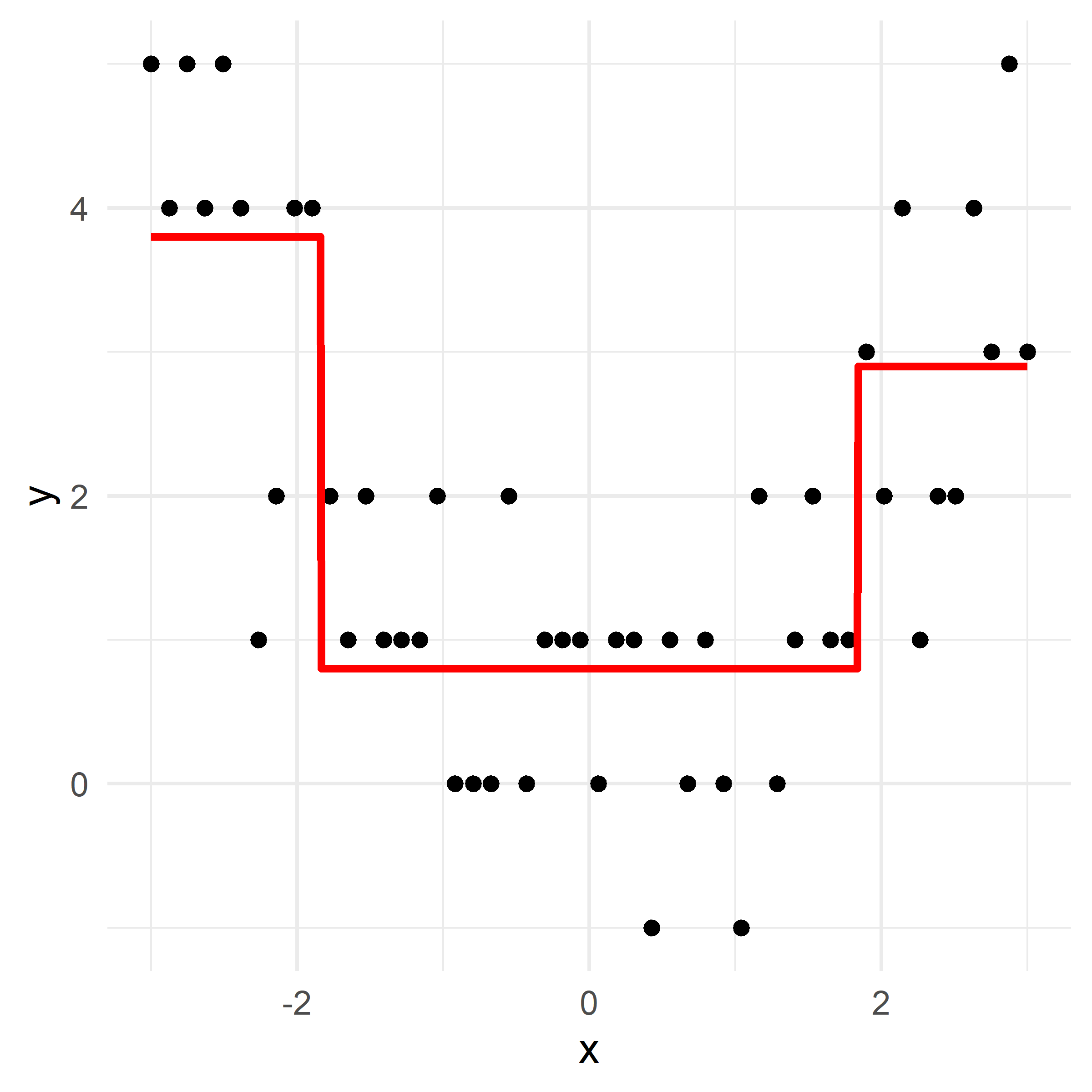
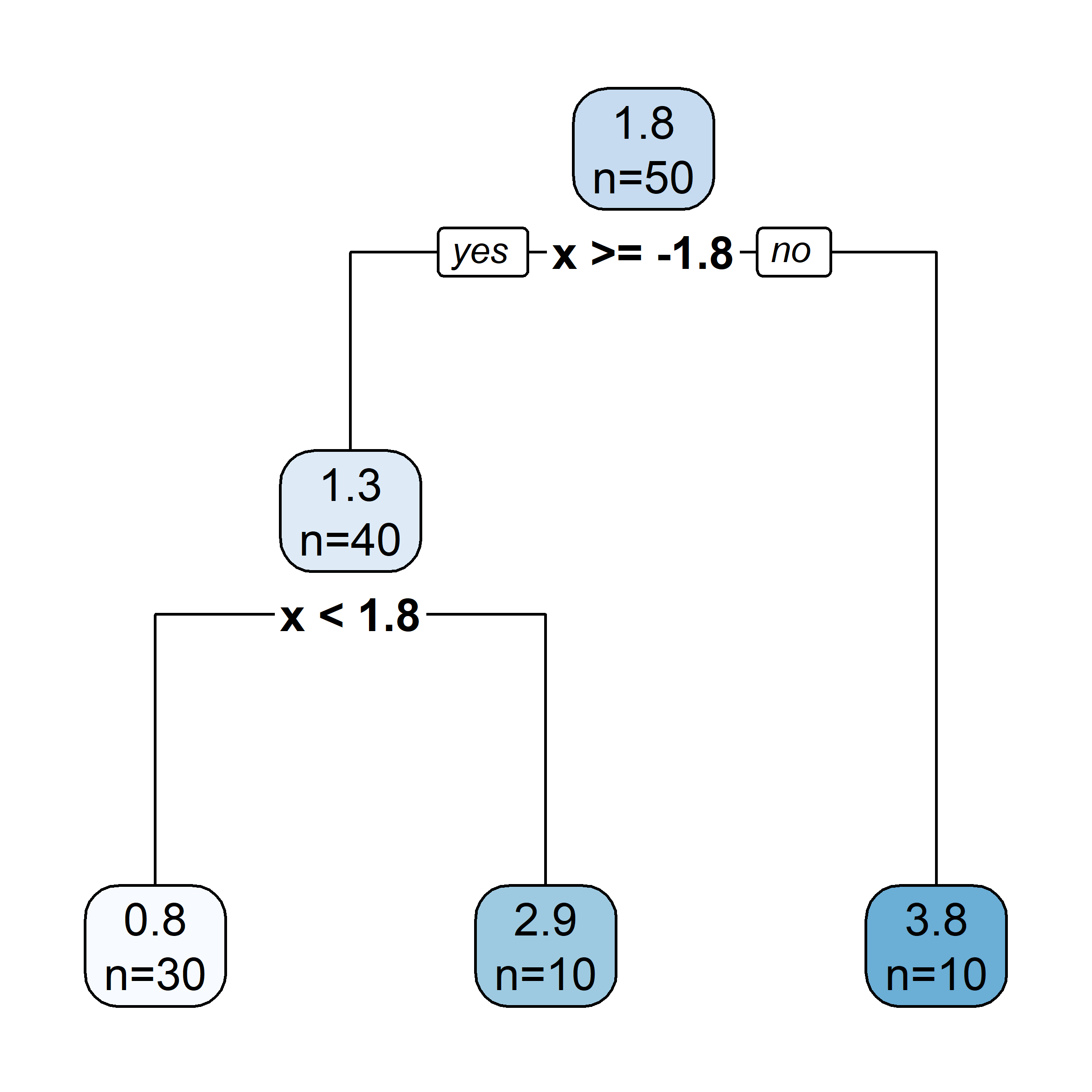
Growing a regression tree IV
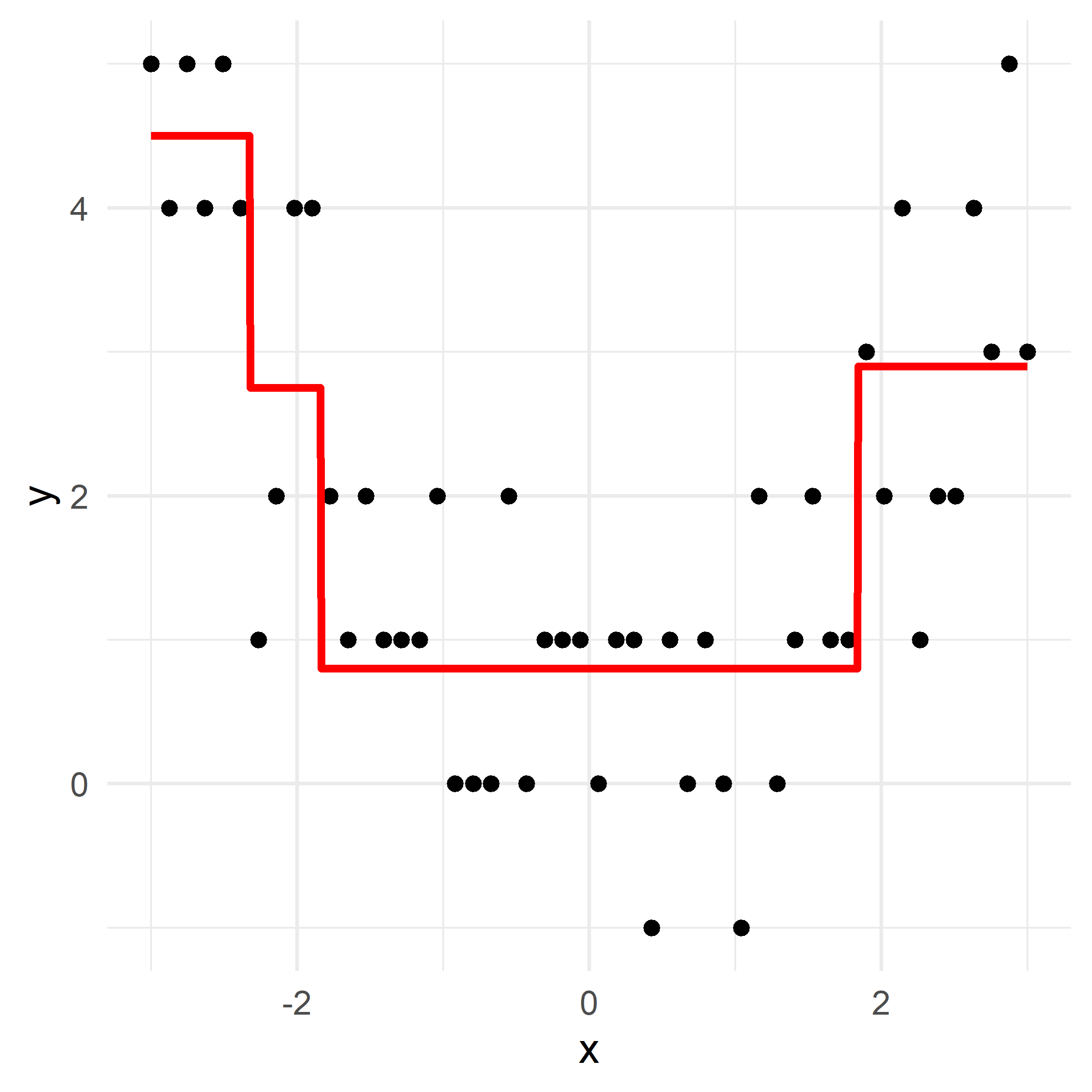
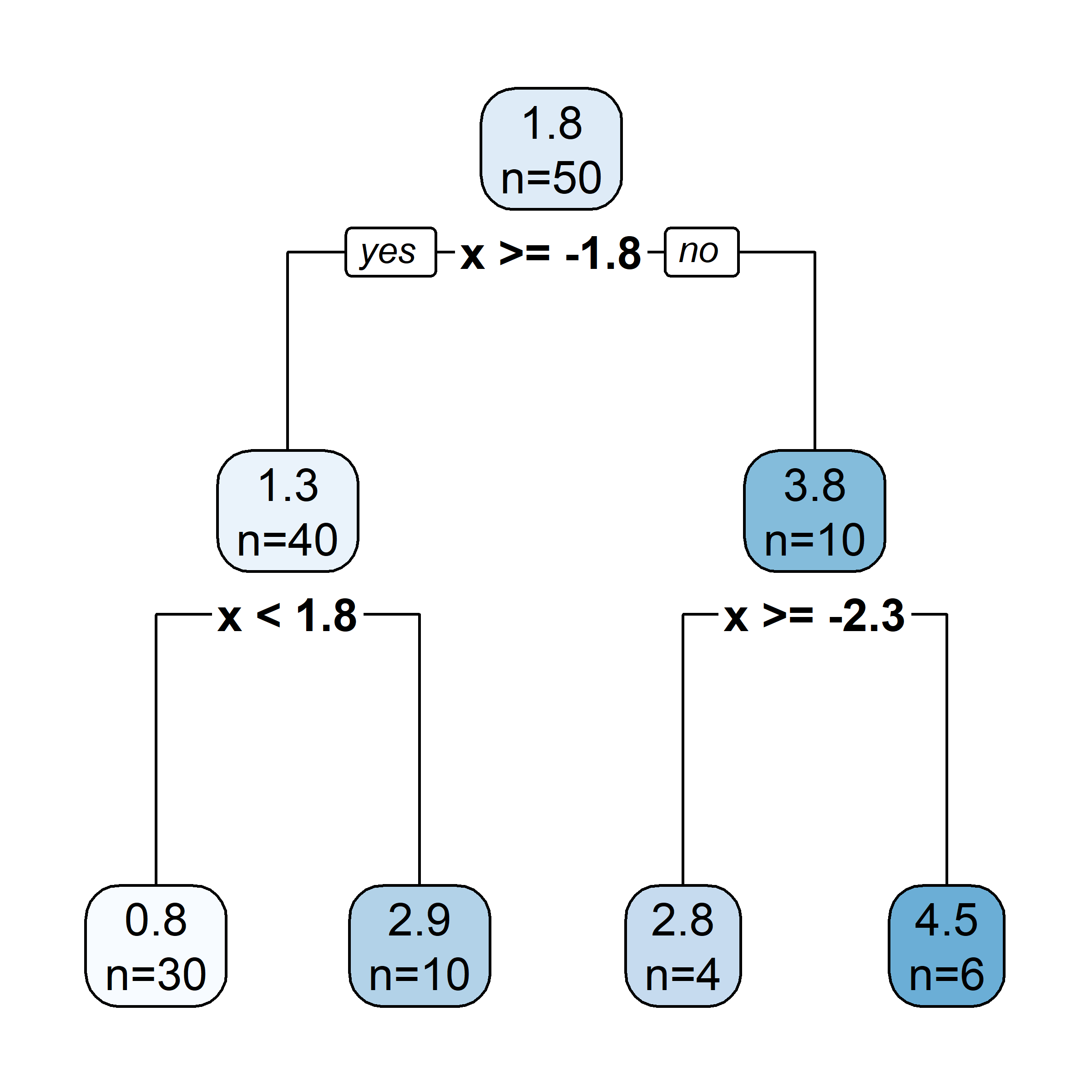
Recursive binary splitting: Overview
- Start with the root node, and make new splits “greedily”, one at a time.
- When choosing what the new split should be:
- consider all of the predictor variables
- for each one, there is an optimal split point s (which, if chosen, maximises the reduction in error)
- computationally, that s can be determined very quickly
- pick the overall best split (i.e., pick the predictor j whose optimal split point s results in the overall largest reduction in error)
- Two new “regions” (aka “leaves”) are hence created.
- Repeat this splitting process (always turning one leaf into two), until a stopping criterion is reached (e.g., each leaf contains \leq 5 observations).
Finding the first “best split”
Consider a splitting variable j and split point s R_1(j, s) = \{X | X_j \leq s\} \quad \text{and} \quad R_2(j, s) = \{X|X_j>s\}
Find the splitting variable j and split point s that solve \min_{j,\ s}\Big[ \min_{c_1} \sum_{x_i \in R_1(j,\ s)}(y_i-c_1)^2 + \min_{c_2} \sum_{x_i \in R_2(j,\ s)}(y_i-c_2)^2 \Big] where the inner mins are solved by \hat{c}_1 = \mathrm{Ave}(y_i | x_i \in R_1(j, s)) \quad \text{and} \quad \hat{c}_2 = \mathrm{Ave}(y_i | x_i \in R_2(j, s))
After this first split, “we repeat the process, looking for the best predictor and best cutpoint in order to split the data further so as to minimize the RSS within each of the resulting regions. However, this time, instead of splitting the entire predictor space, we split one of the two previously identified regions.” (James et al., 2021)
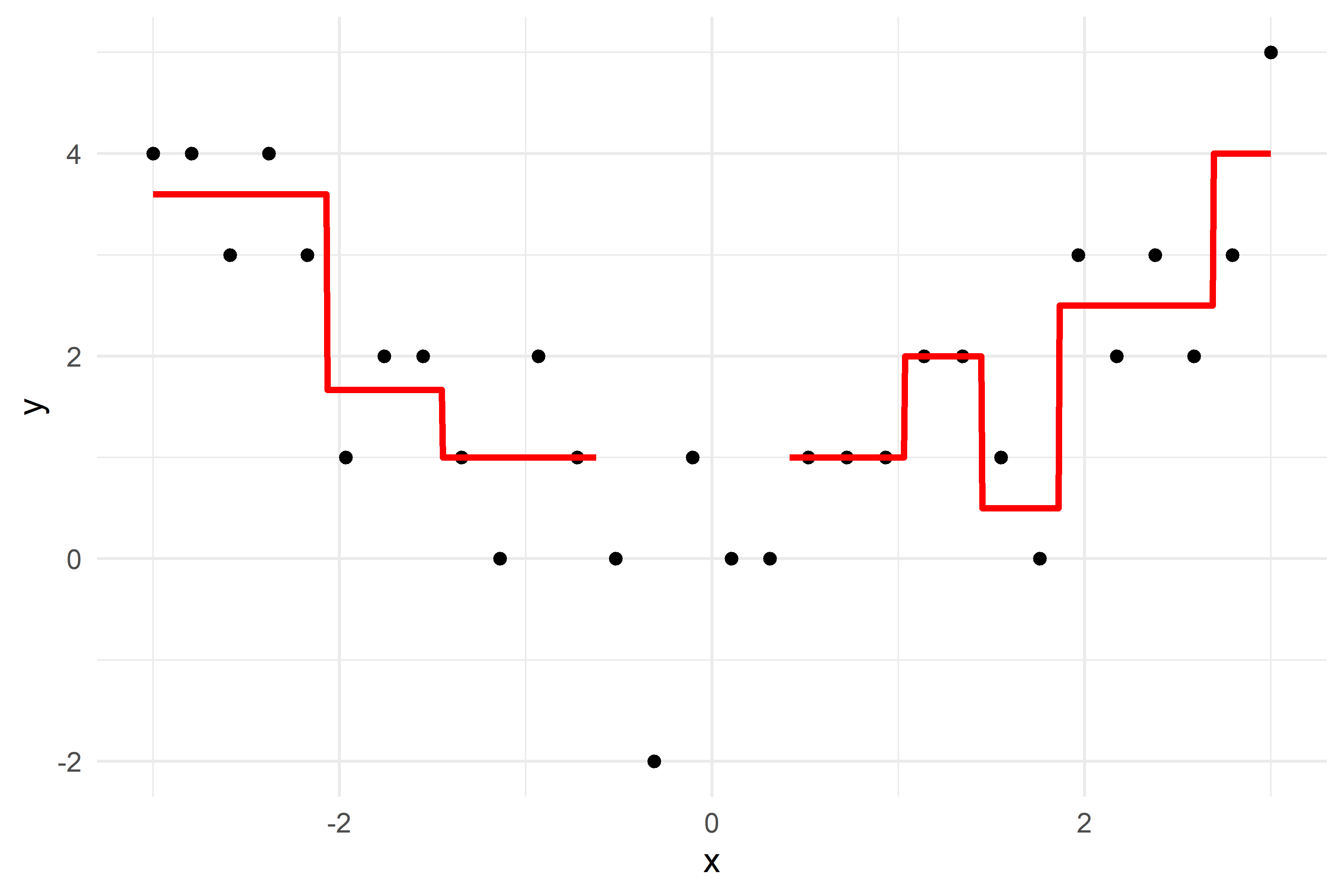
2023 exam question
What would be the tree’s predicted value for y at x = 0?
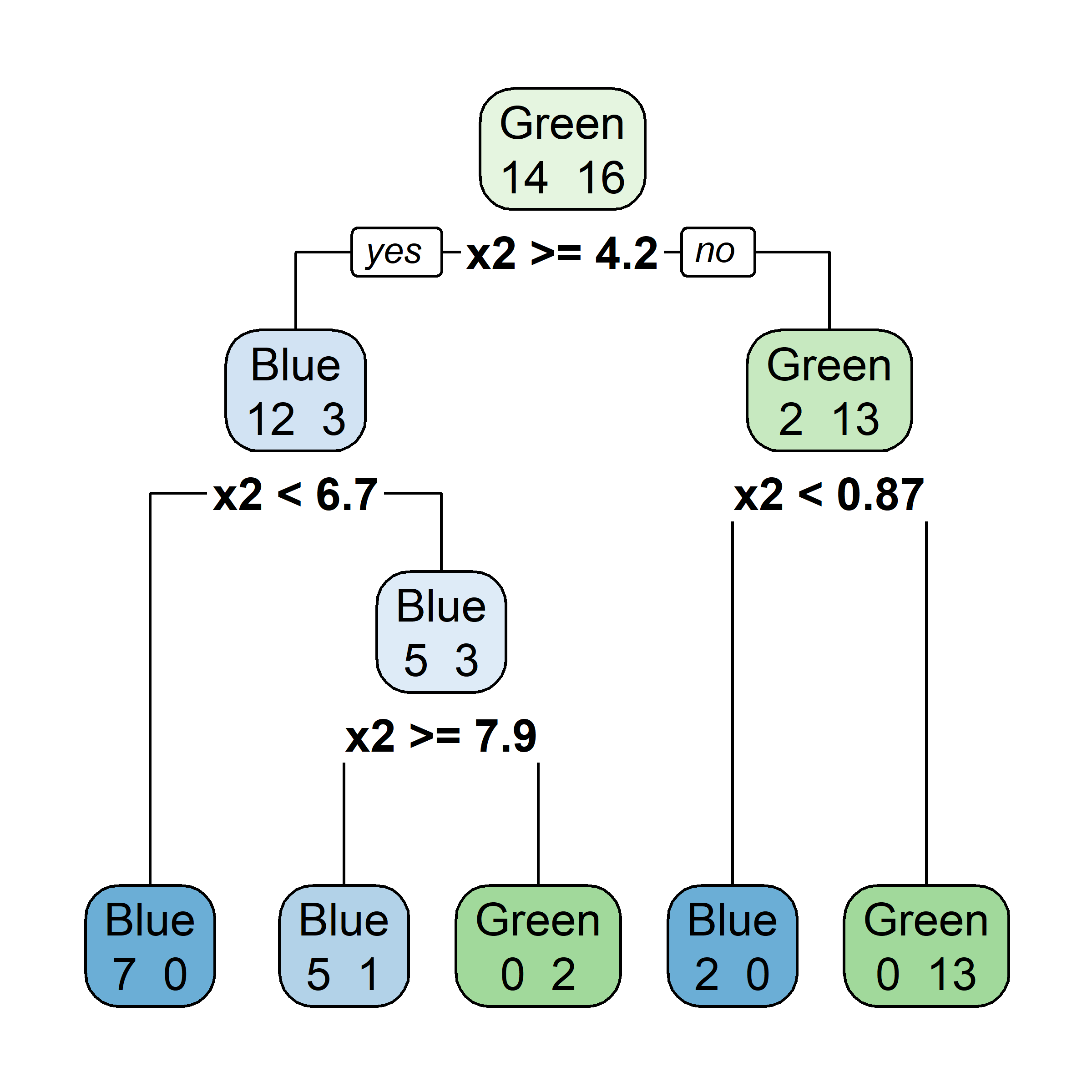
Classification trees
Very similar to a regression tree, except:
- Predict that each observation belongs to the most commonly occurring class (mode) of training observations in the region to which it belongs.
- RSS cannot be used as a criterion for making the binary splits, instead we use a measure of node purity (small values are “good”). For a given region R_m, compute either:
Gini index, or
G = \sum_{k=1}^{K}\hat{p}_{mk}(1 - \hat{p}_{mk})
entropy
D = -\sum_{k=1}^{K}\hat{p}_{mk}\ln(\hat{p}_{mk})
where \hat{p}_{mk} = \frac{1}{| R_m | }\sum_{x_i \in R_m}I(y_i = k) \,.
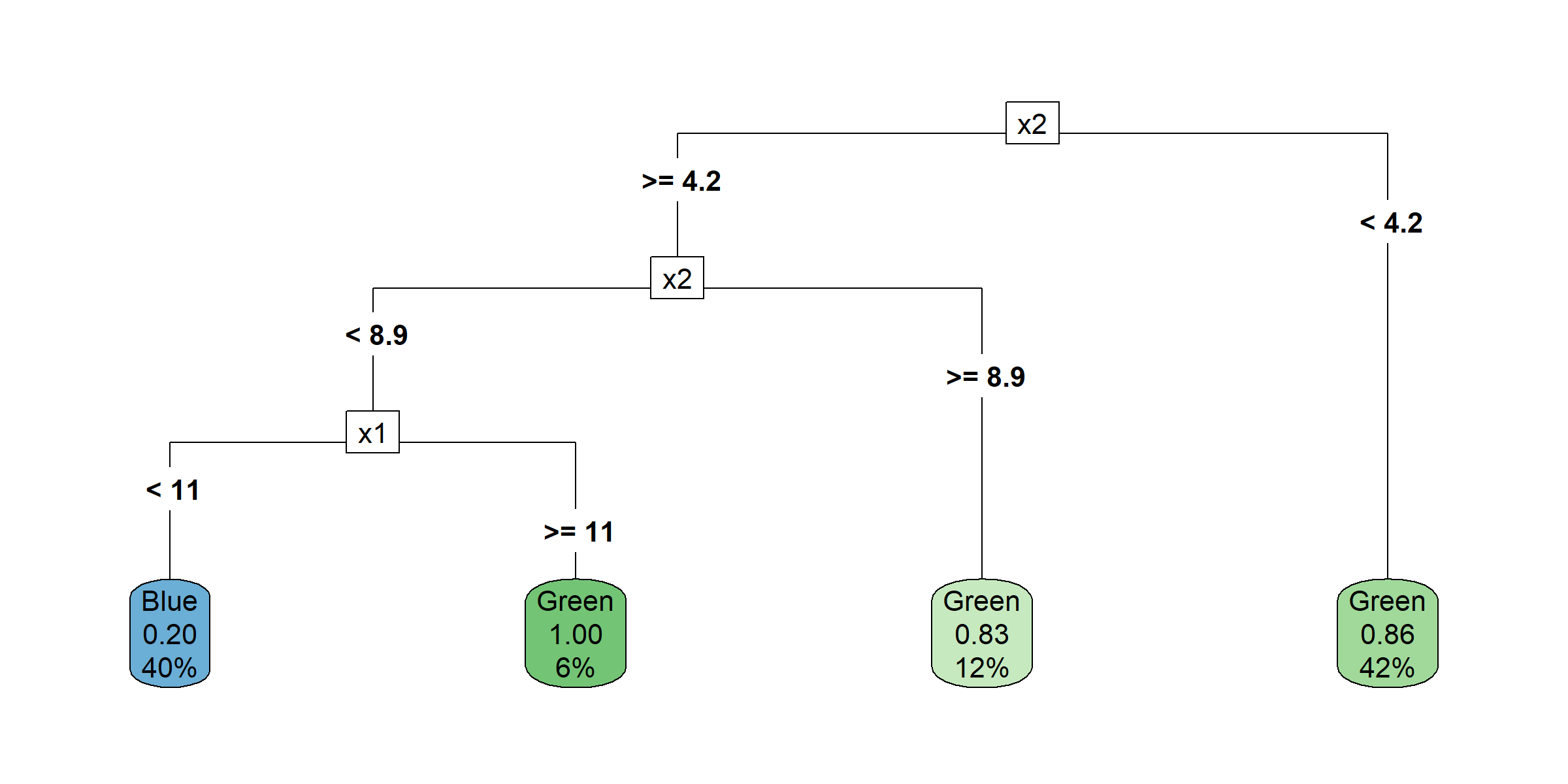
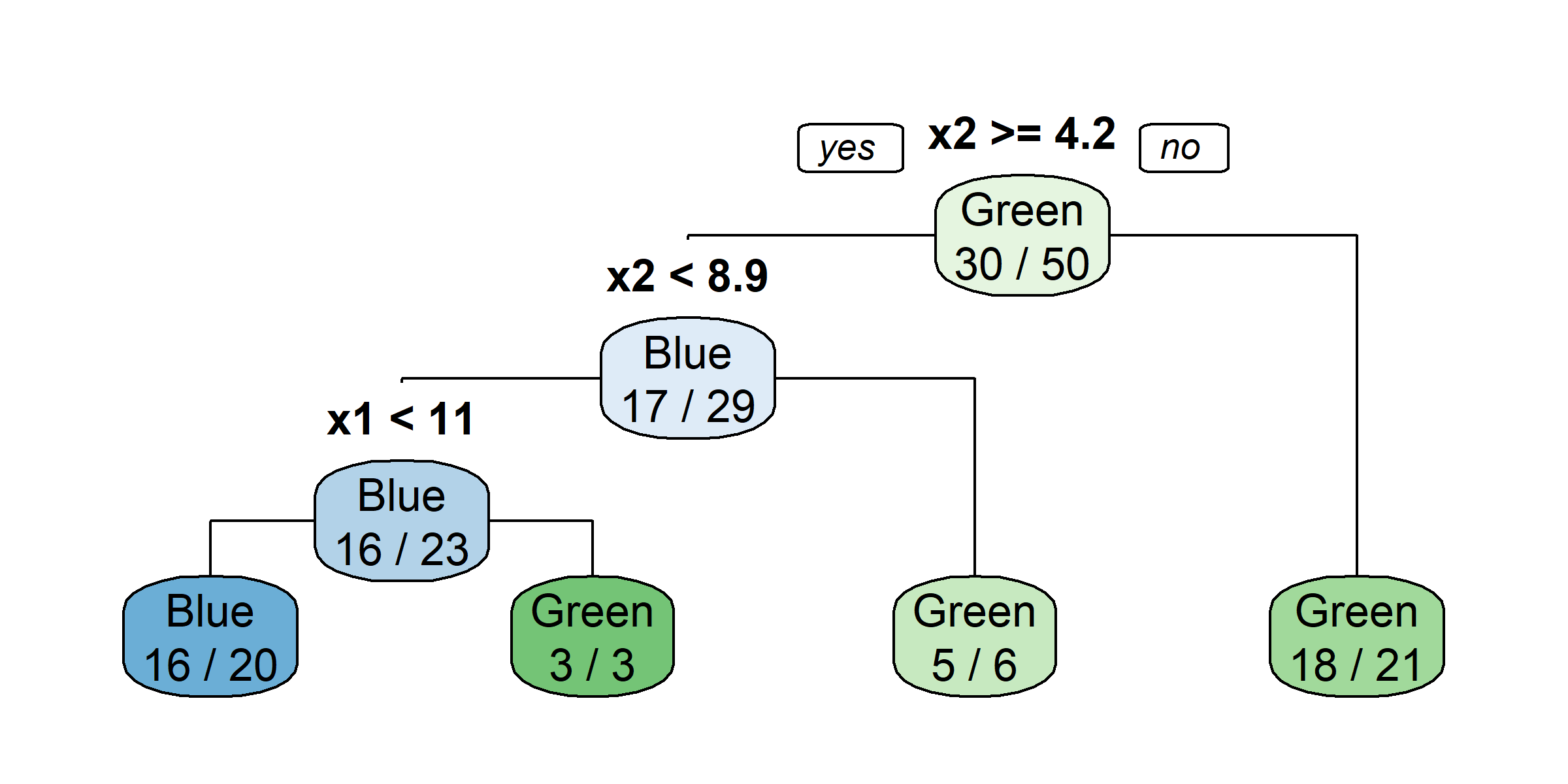
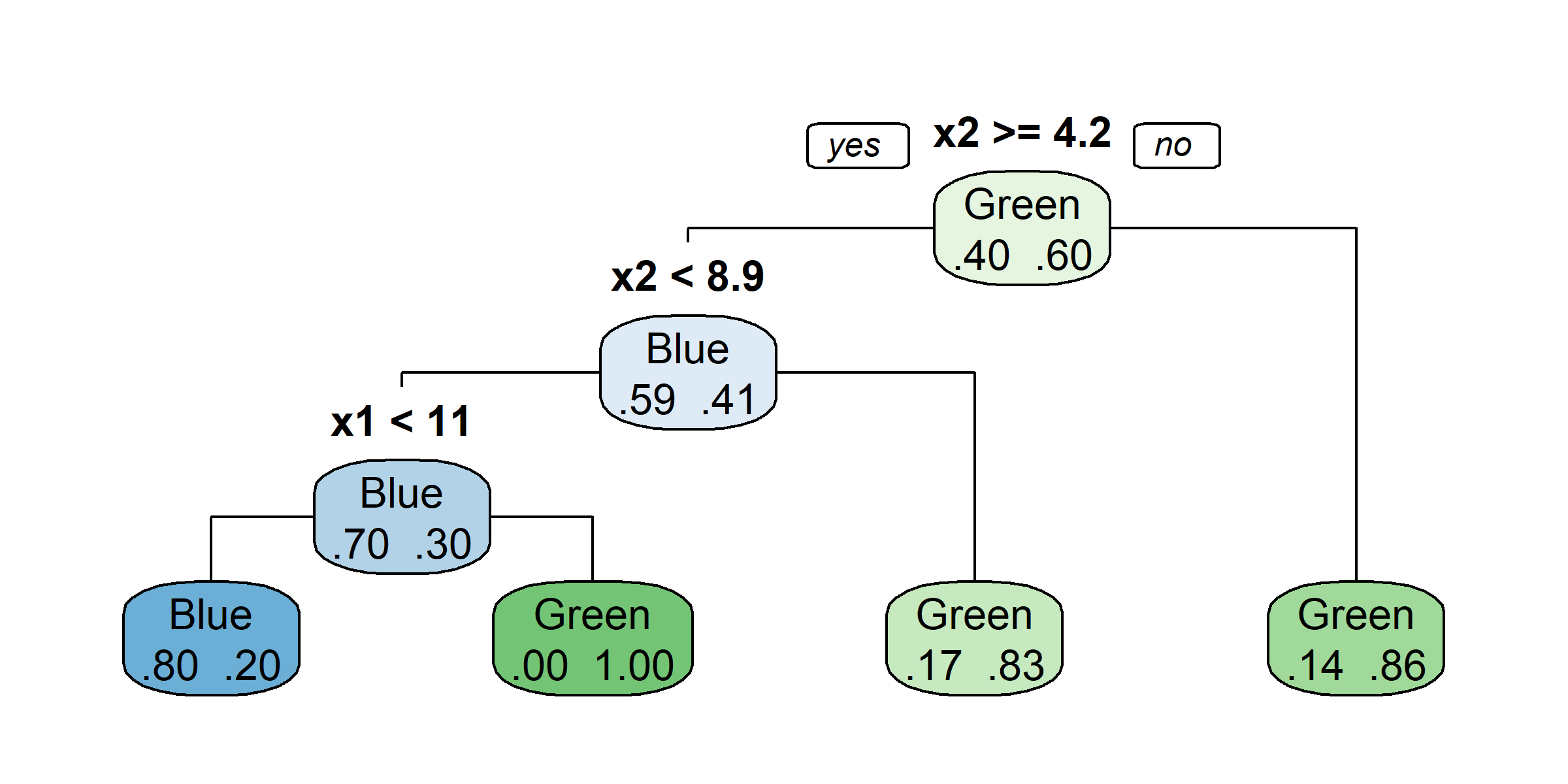
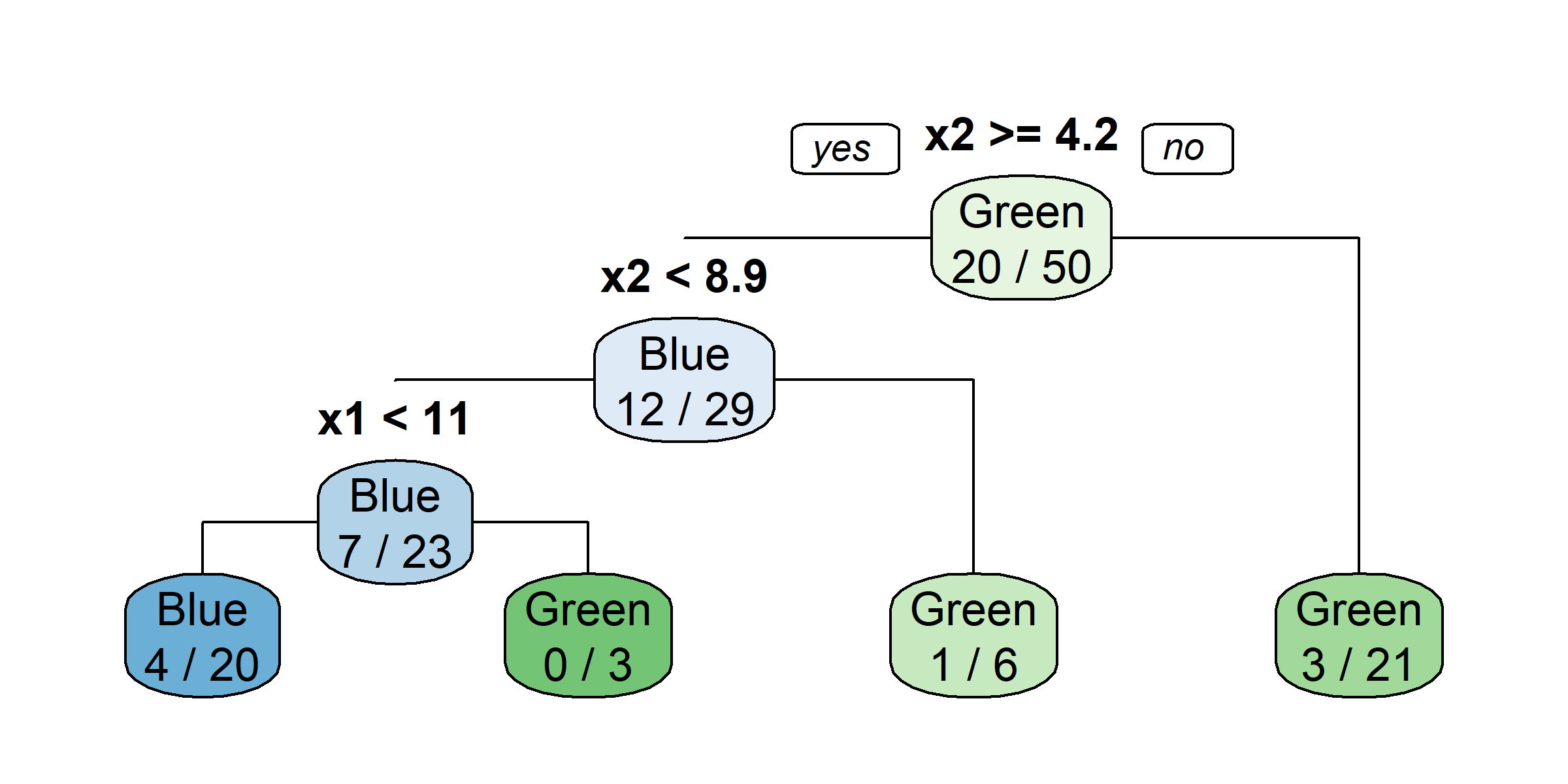
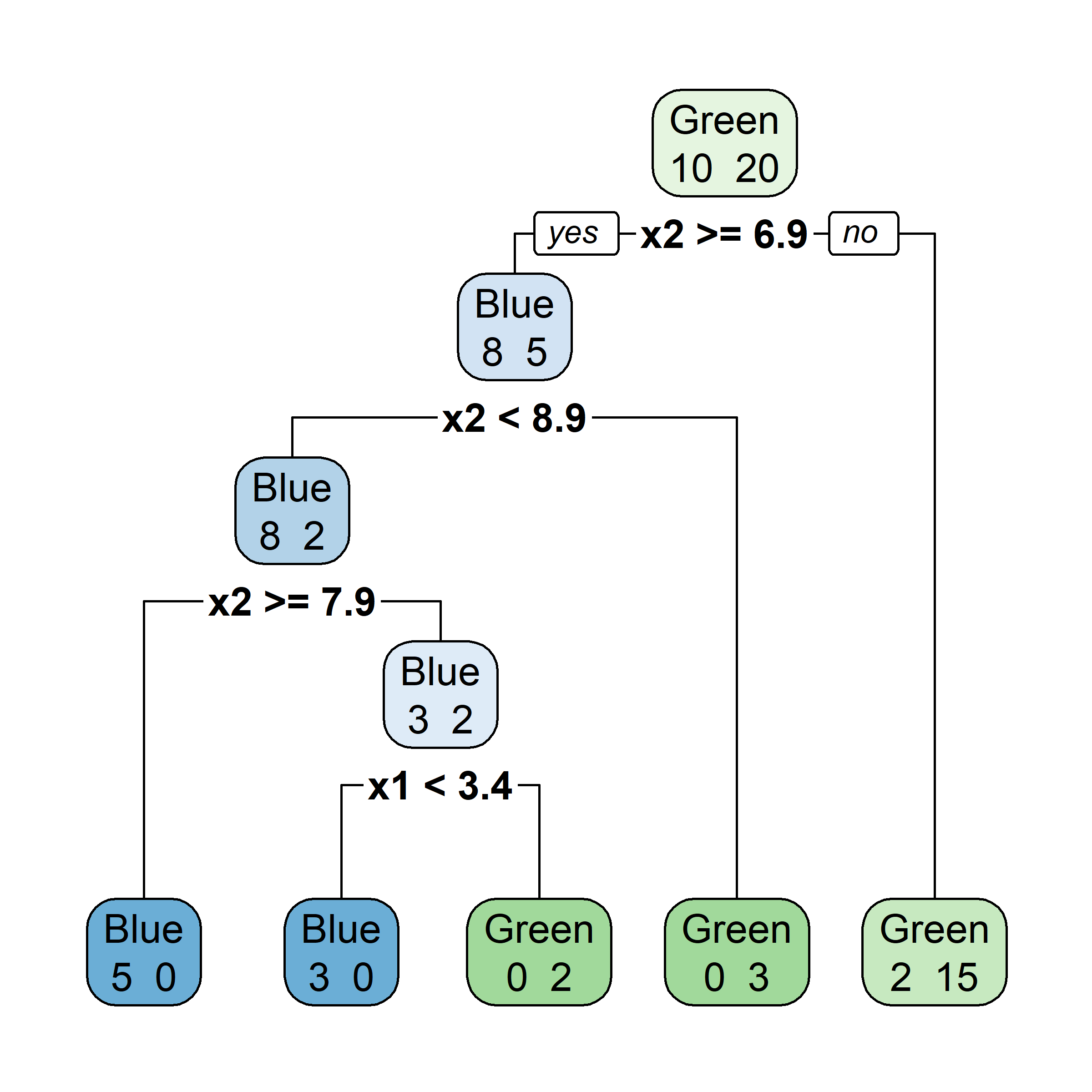
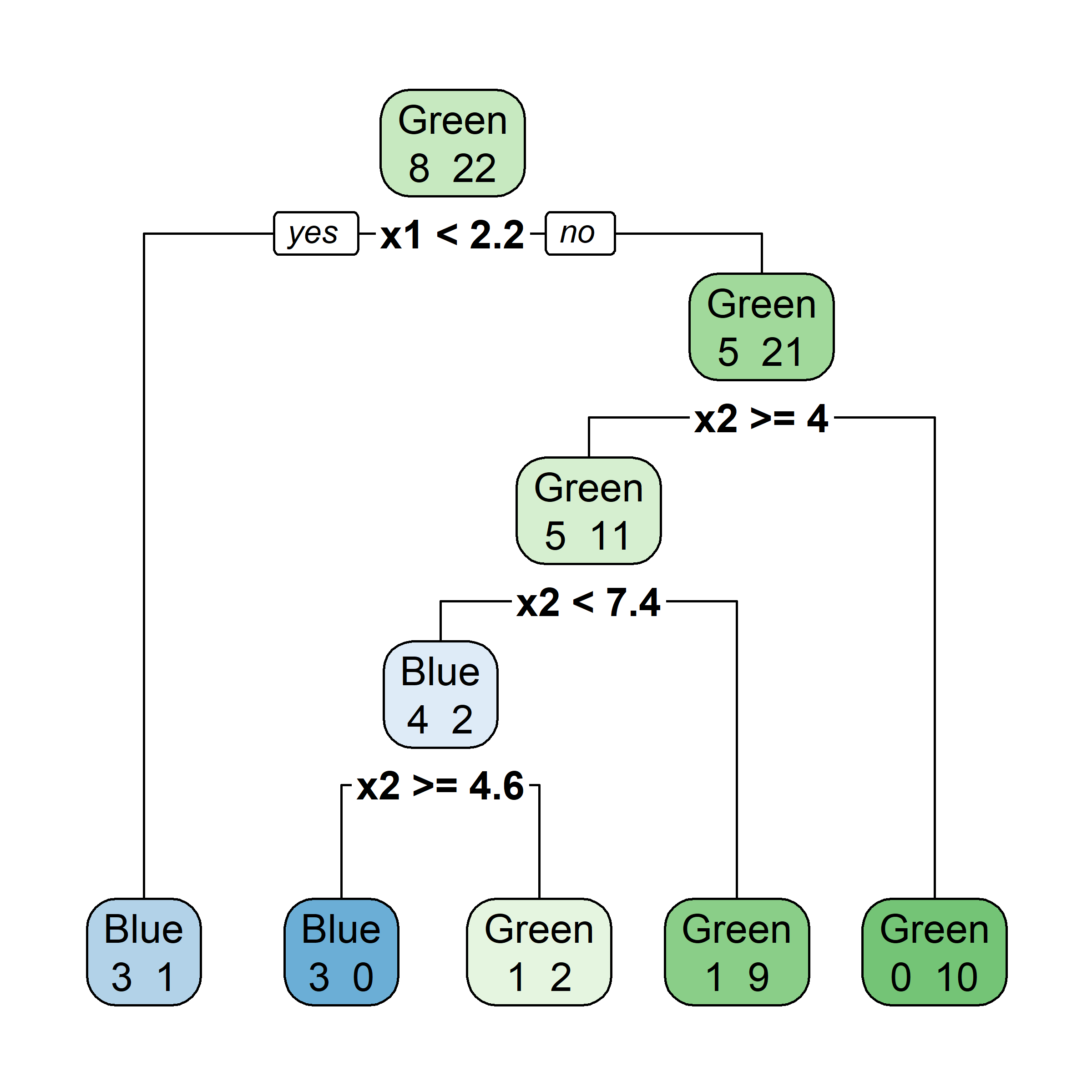
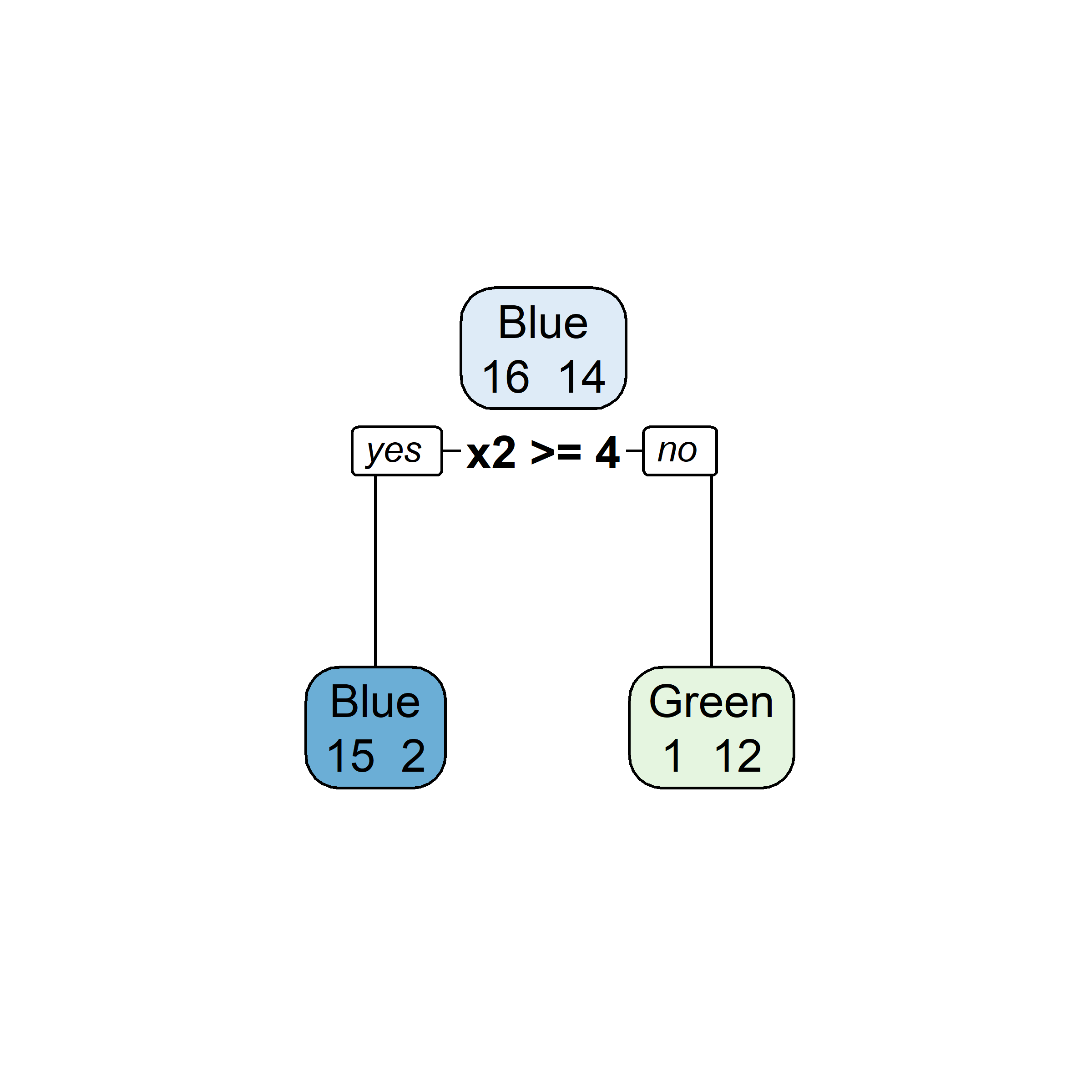
Growing a classification tree I
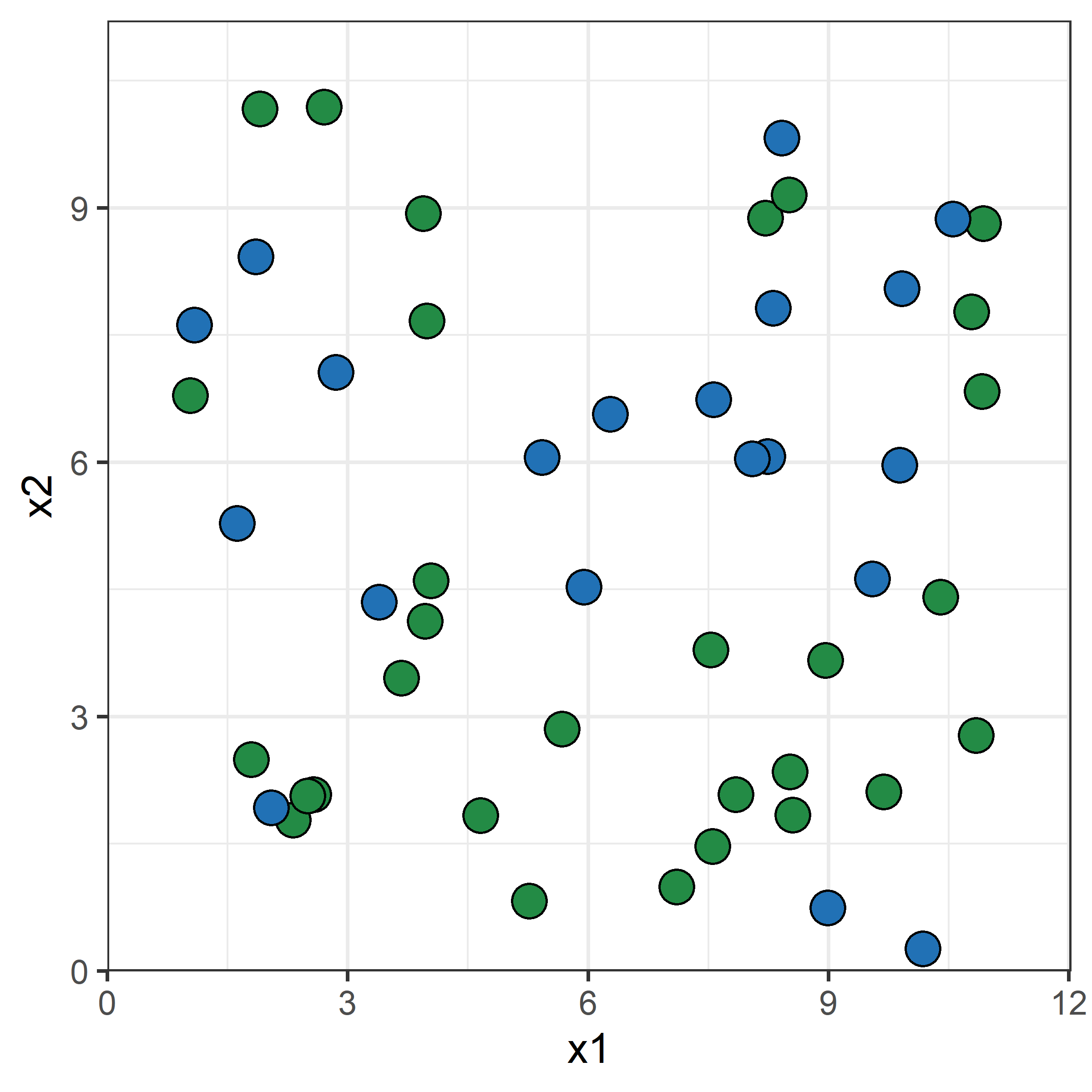
Growing a classification tree II
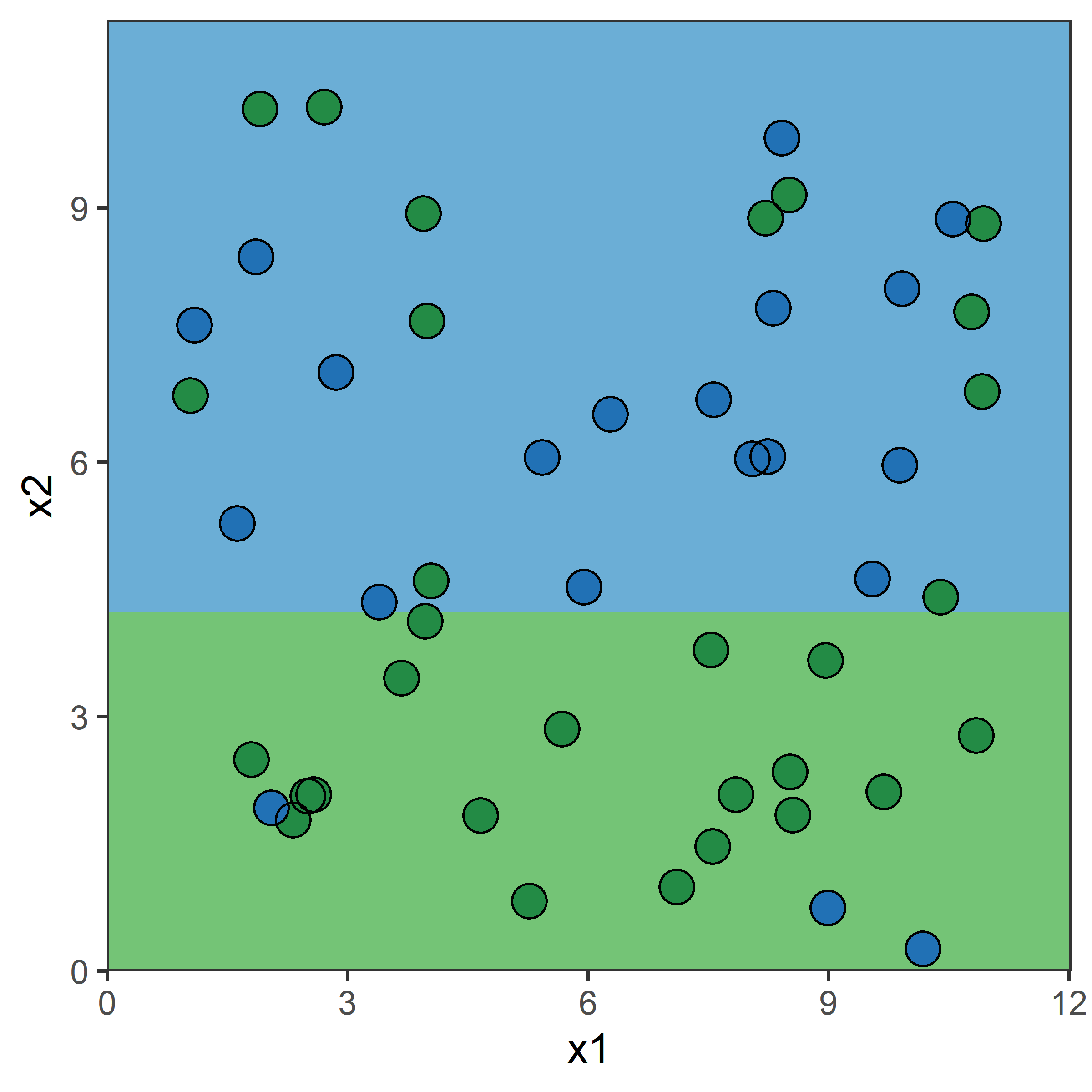
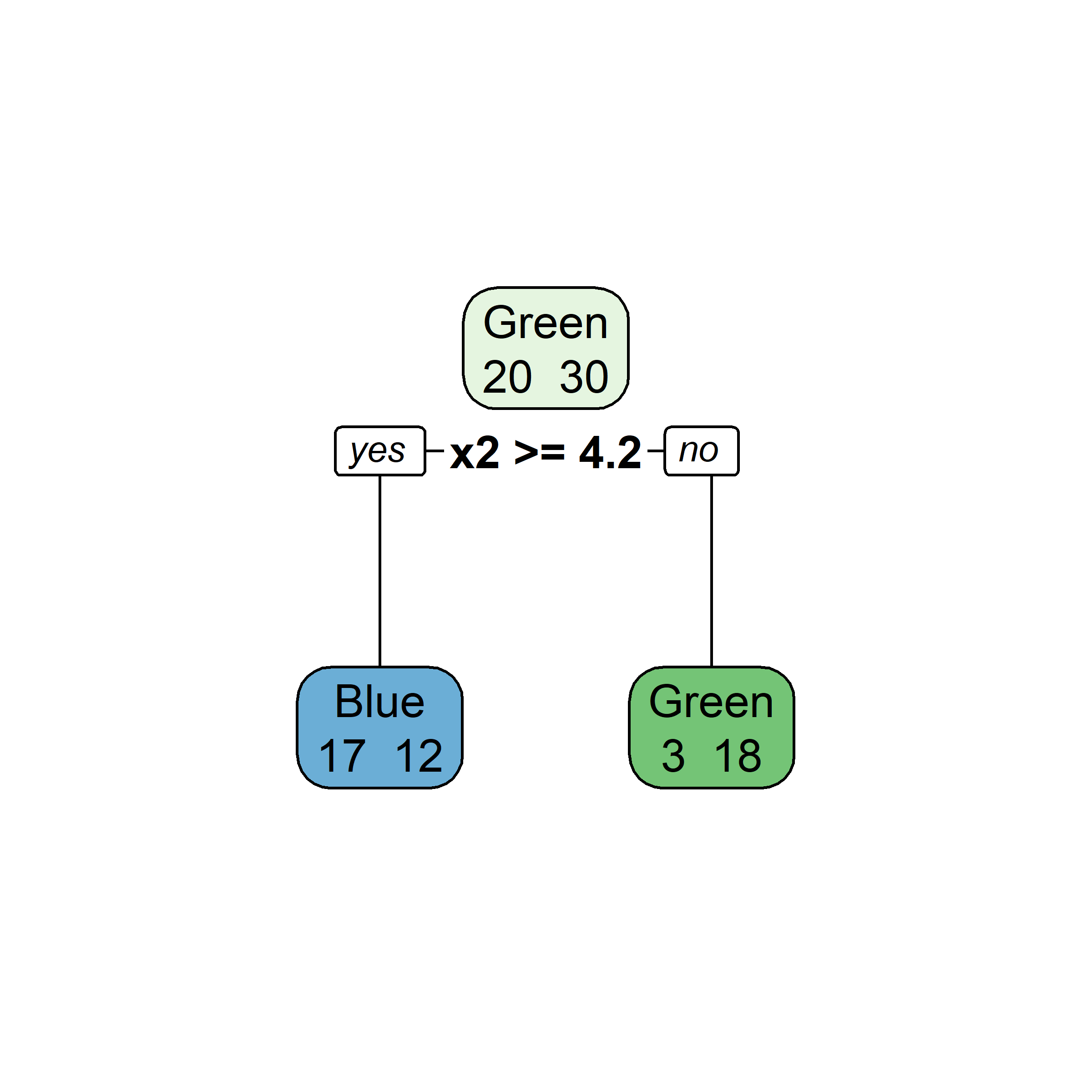
Growing a classification tree III
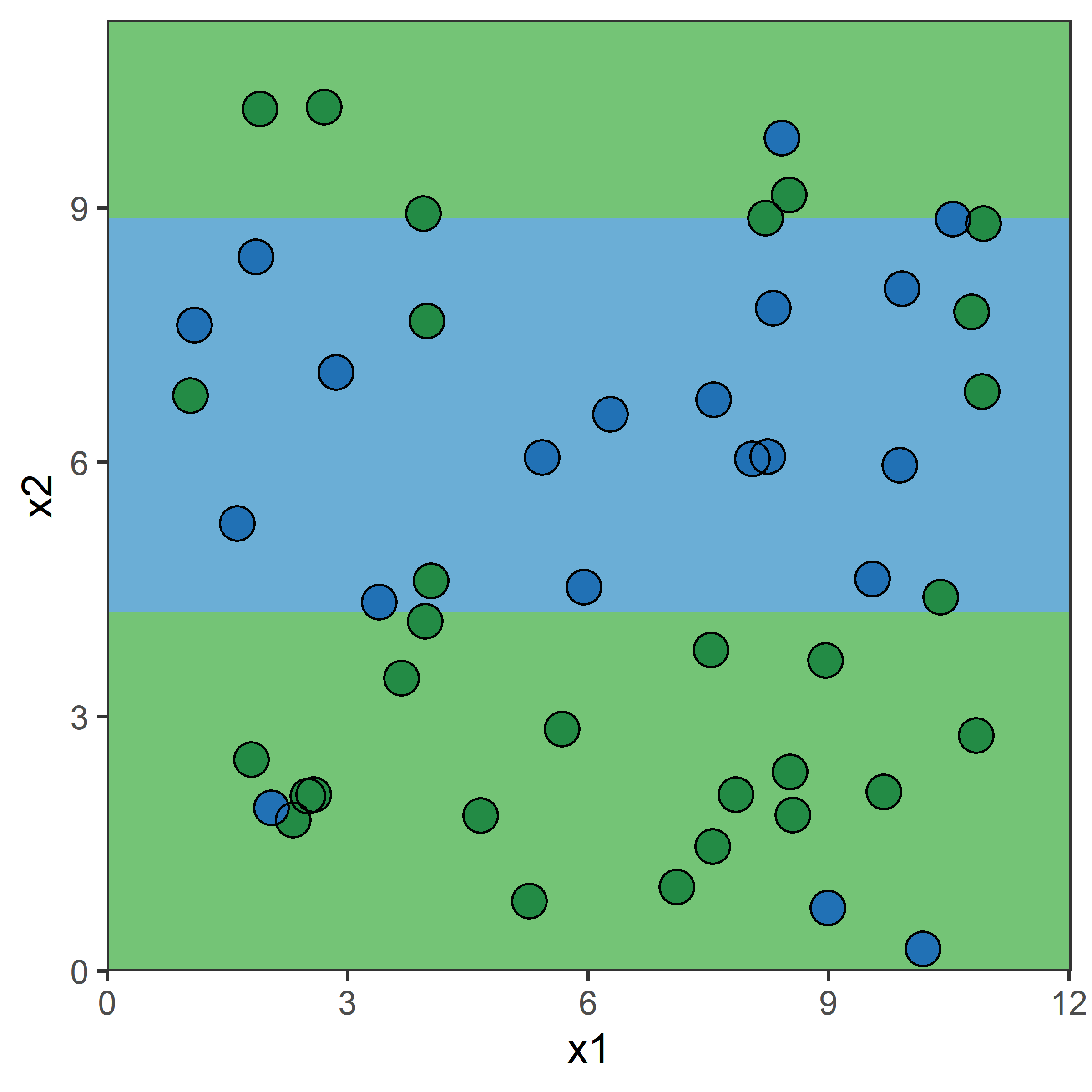
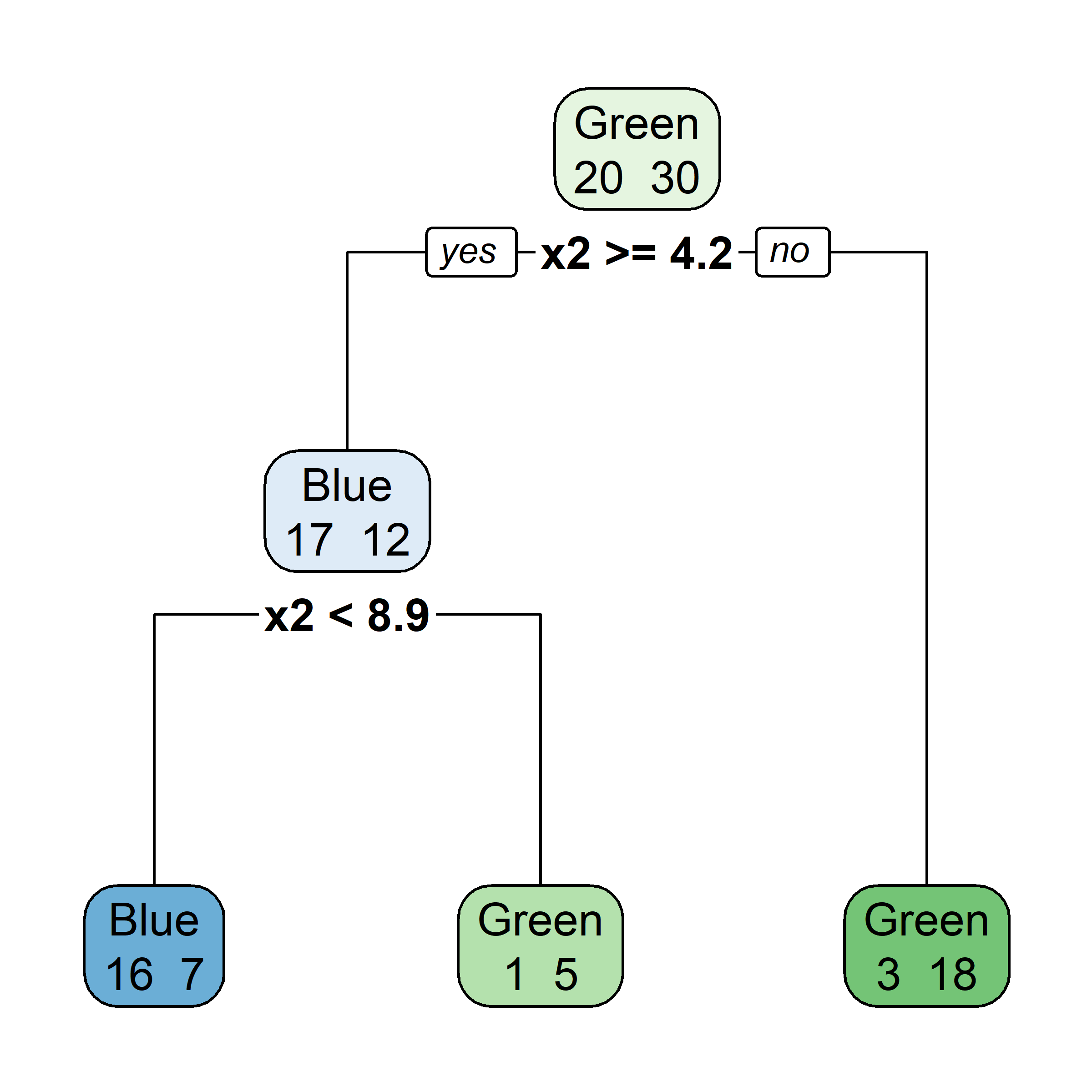
Growing a classification tree IV
Multiple representations
Multiple representations II
Which one?
So, should you use Gini impurity or entropy? The truth is, most of the time it does not make a big difference: they lead to similar trees. Gini impurity is slightly faster to compute, so it is a good default. However, when they differ, Gini impurity tends to isolate the most frequent class in its own branch of the tree, while entropy tends to produce slightly more balanced trees.
See also Sebastian Raschka’s interesting analysis for more details.
Source: Géron (2022), Chapter 6.
National Flood Insurance Program Demo
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
National Flood Insurance Program
Available at OpenFEMA dataset.

National Flood Insurance Program (NFIP, image source)
See also Zhang and Xu (2023), Fairness of Ratemaking for Catastrophe Insurance: Lessons from Machine Learning, Information Systems Research.
The data dictionary
| Name | Title | Type | Description |
|---|---|---|---|
| id | ID | text | Unique ID assigned to the record |
| amountPaidOnBuildingClaim | Amount Paid on Building Claim | decimal | Dollar amount paid on the building claim. In some instances, a negative amount may appear. |
| agricultureStructureIndicator | Agriculture Structure Indicator | boolean | Indicates whether a building is reported as being an agricultural structure in the policy application. |
| policyCount | Policy Count | smallint | Insured units in an active status. A policy contract ceases to be in an active status as of the cancellation date or the expiration date. |
| countyCode | County Code | text | FIPS code uniquely identifying the primary County (e.g., 011 represents Broward County) associated with the project. |
| lossDate | Date of Loss | datetime | Date on which water first entered the insured building. |
| elevatedBuildingIndicator | Elevated Building Indicator | boolean | Indicates whether a building meets the NFIP definition of an elevated building. |
| latitude | Latitude | decimal | Approximate latitude of the insured building. |
| locationOfContents | Location of Contents | smallint | Code that indicates the location of contents, (e.g., garage on property, in house). |
| Name | Title | Type | Description |
|---|---|---|---|
| longitude | Longitude | decimal | Approximate longitude of the insured building. |
| lowestFloorElevation | Lowest Floor Elevation | decimal | A building’s lowest floor is the floor or level that is used as the point of reference when rating a building. |
| numberOfFloors | Number of Floors | smallint | Code that indicates the number of floors in the insured building. |
| occupancyType | Occupancy Type | smallint | Code indicating the use and occupancy type of the insured structure. |
| originalConstructionDate | Original Construction Date | date | The original date of the construction of the building. |
| originalNBDate | Original NB Date | date | The original date of the flood policy. |
| postFIRMConstructionIndicator | Post-FIRM Construction Indicator | boolean | Indicates whether construction was started before or after publication of the FIRM. |
| rateMethod | Rate Method | text | Indicates policy rating method. |
| state | State | text | The two-character alpha abbreviation of the state in which the insured property is located. |
| totalBuildingInsuranceCoverage | Total Building Insurance Coverage | integer | Total Insurance Amount in whole dollars on the Building. |
First decision tree
Remove ID column
Dates to years and months
Code
claims$lossYear <- year(claims$lossDate)
claims$lossMonth <- month(claims$lossDate)
claims$lossDate <- NULL
claims$originalConstructionYear <- year(claims$originalConstructionDate)
claims$originalConstructionMonth <- month(claims$originalConstructionDate)
claims$originalConstructionDate <- NULL
claims$originalNBYear <- year(claims$originalNBDate)
claims$originalNBMonth <- month(claims$originalNBDate)
claims$originalNBDate <- NULL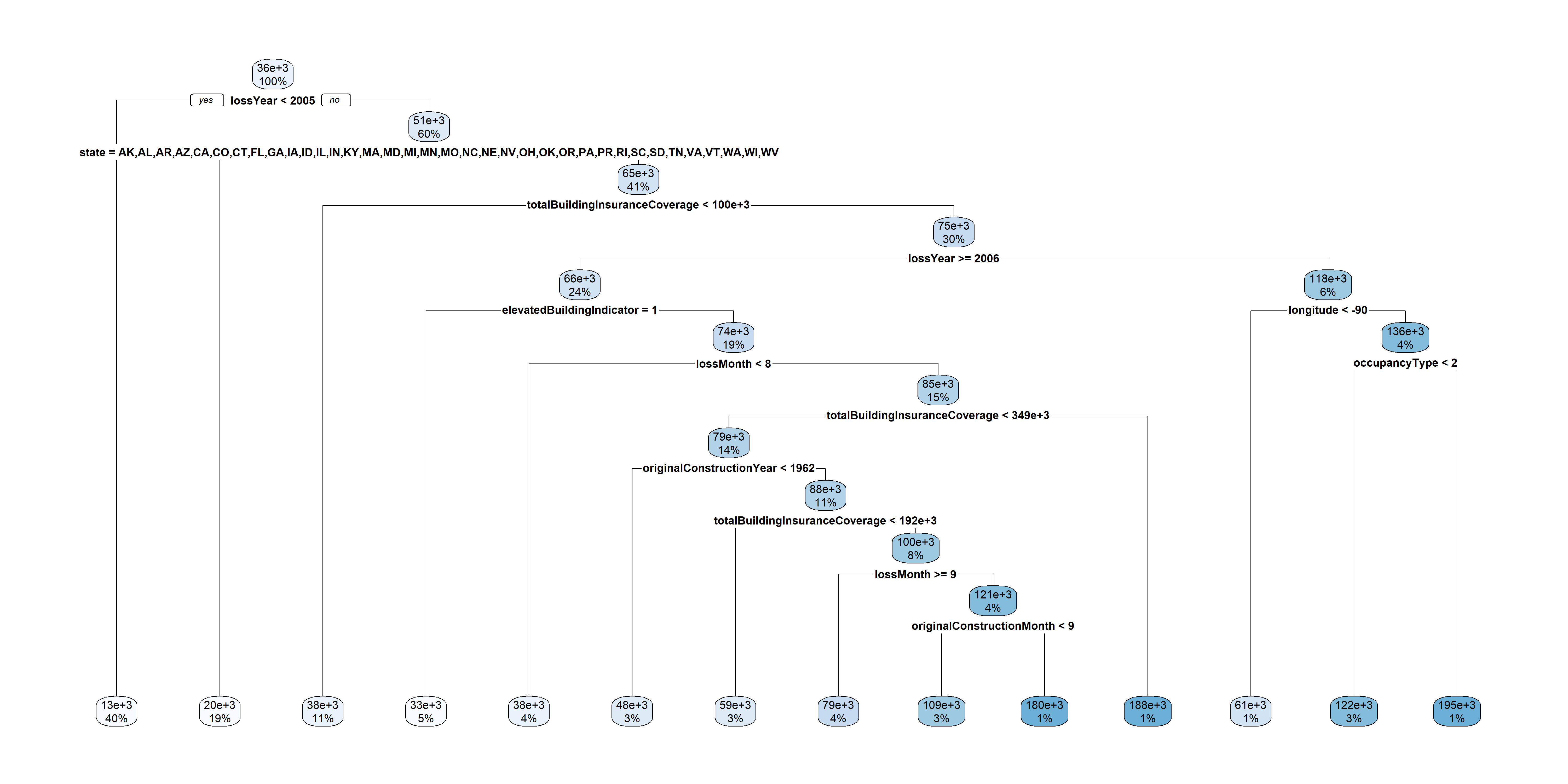
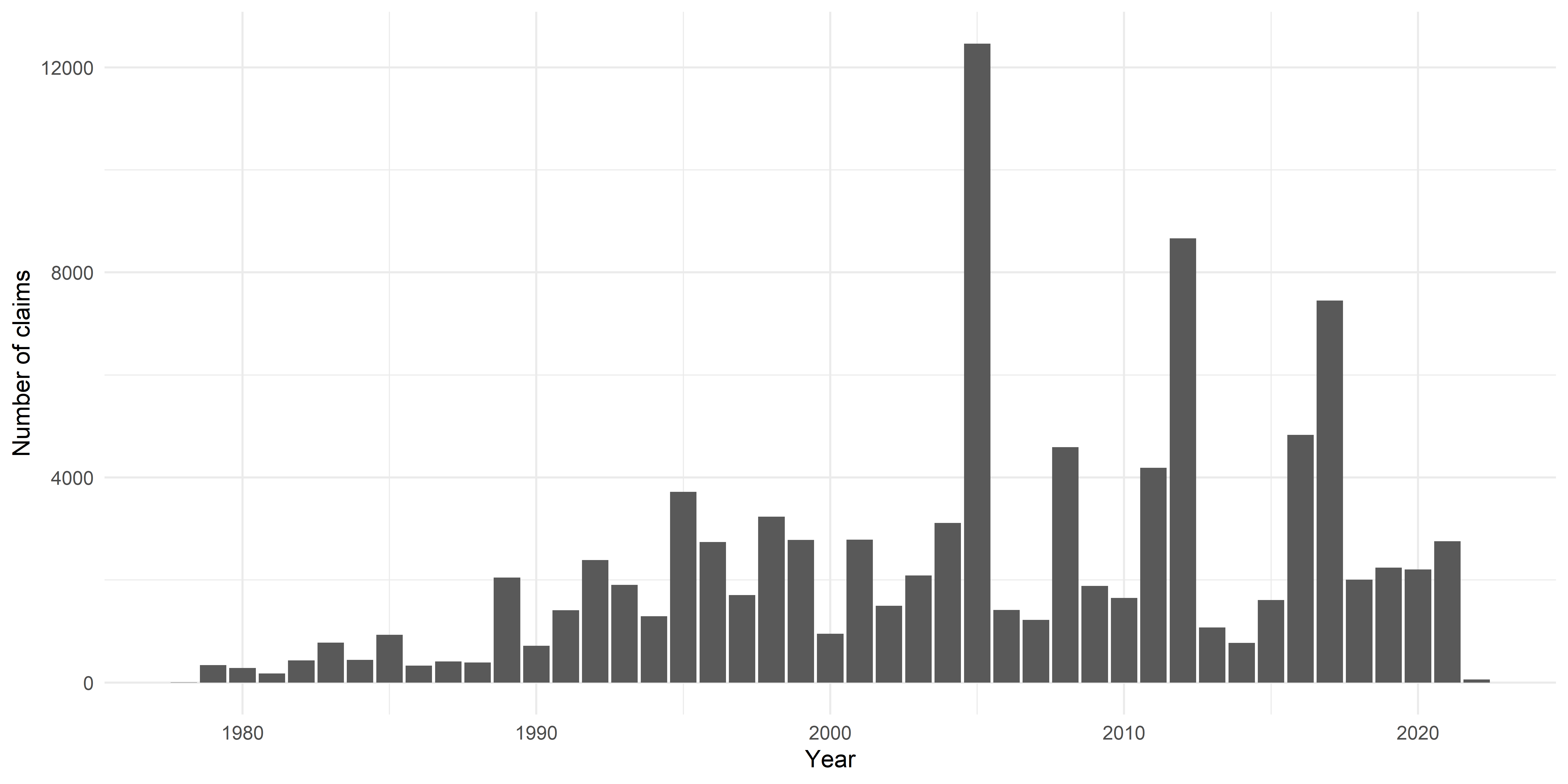
Plot claims by year
Plot average claim size by year
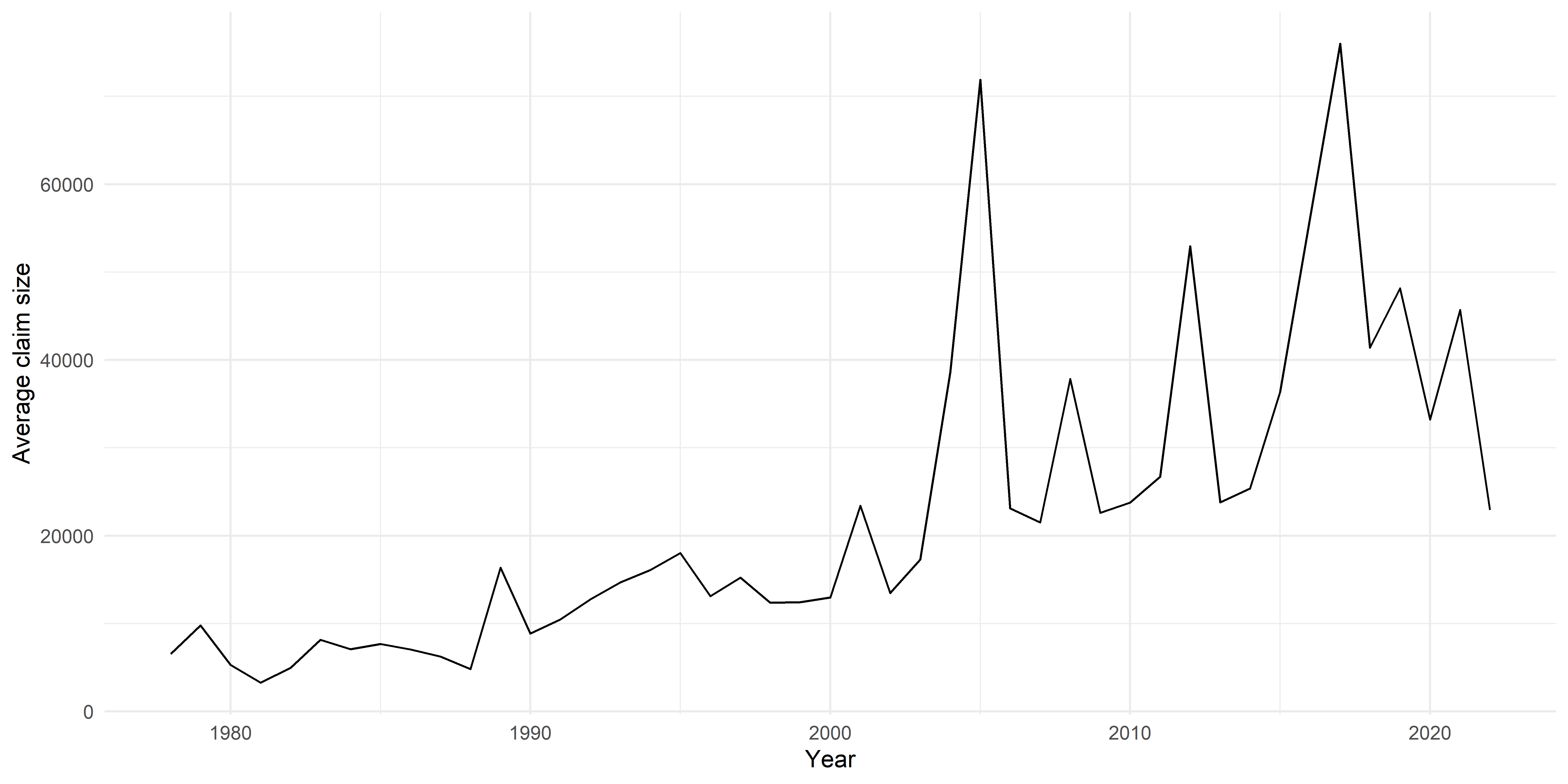
Number of claims by state
Prepare to make state-based maps for USA
claims$state_full <- state.name[match(claims$state, state.abb)]
state_claims <- claims %>%
group_by(state_full) %>%
summarise(num_claims = n(),
max_claim_size = max(amountPaidOnBuildingClaim),
common = num_claims >= nrow(claims) / 100)
claims$state_full <- NULL
# Merge with the map data
states_map <- map_data("state")
state_claims$region <- tolower(state_claims$state_full)
states_map <- left_join(states_map, state_claims, by = "region")Code
ggplot(states_map, aes(long, lat, group = group, fill = num_claims)) +
geom_polygon(color = "white") +
scale_fill_viridis_c(option = "C") +
labs(title = "Number of Claims by State",
fill = "Number of Claims") +
theme_minimal() +
theme(axis.title = element_blank(), axis.text = element_blank(), axis.ticks = element_blank())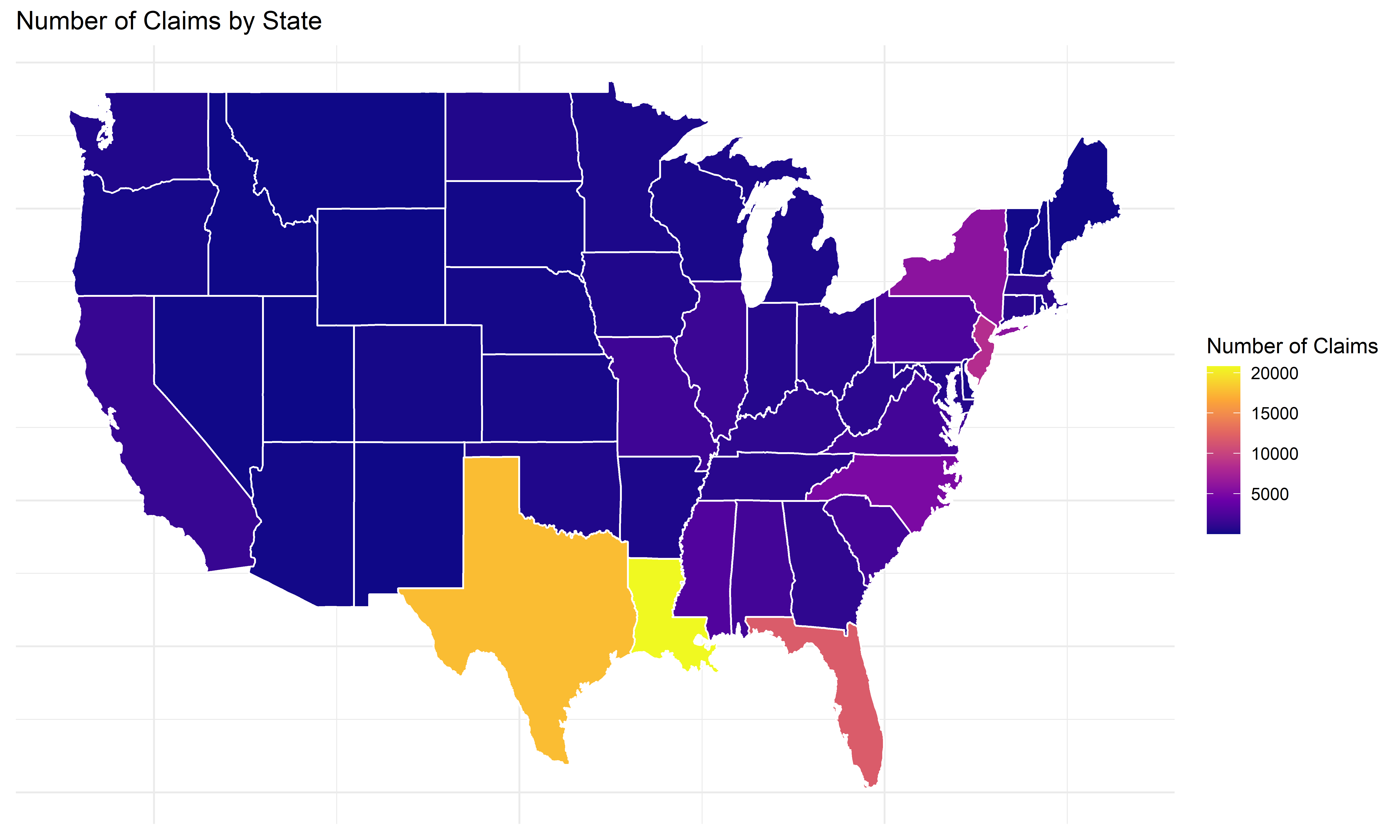
Max claim size by state
Code
# Plot maximum claim size by state
ggplot(states_map, aes(long, lat, group = group, fill = max_claim_size)) +
geom_polygon(color = "white") +
scale_fill_viridis_c(option = "C") +
labs(title = "Maximum Claim Size by State",
fill = "Max Claim Size") +
theme_minimal() +
theme(axis.title = element_blank(), axis.text = element_blank(), axis.ticks = element_blank())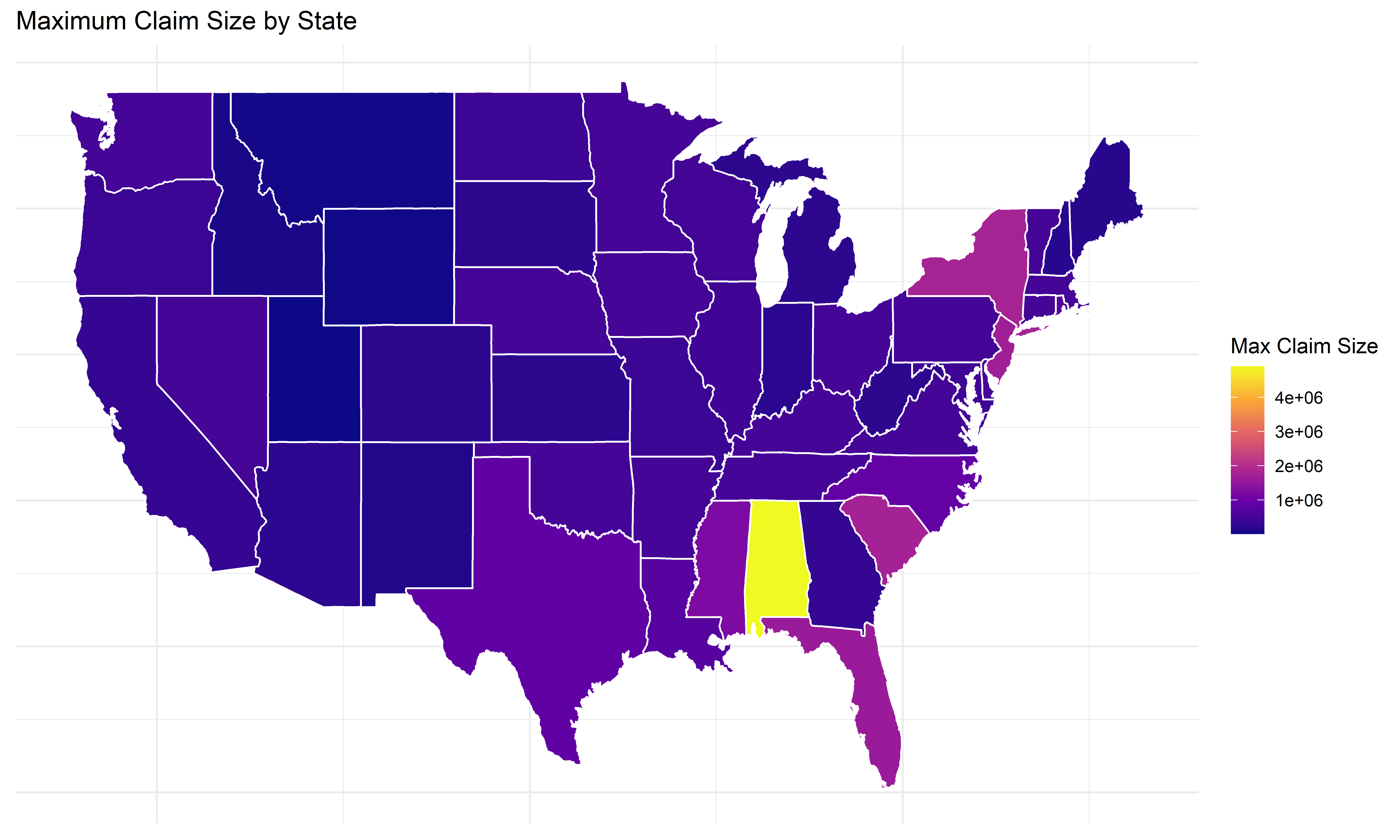
Some states have very few claims
Code
# Plot states where floods are common
ggplot(states_map, aes(long, lat, group = group, fill = common)) +
geom_polygon(color = "white") +
scale_fill_viridis_d() +
labs(title = "States where flood claims are frequent",
fill = "Number of Claims >= 1%") +
theme_minimal() +
theme(axis.title = element_blank(), axis.text = element_blank(), axis.ticks = element_blank())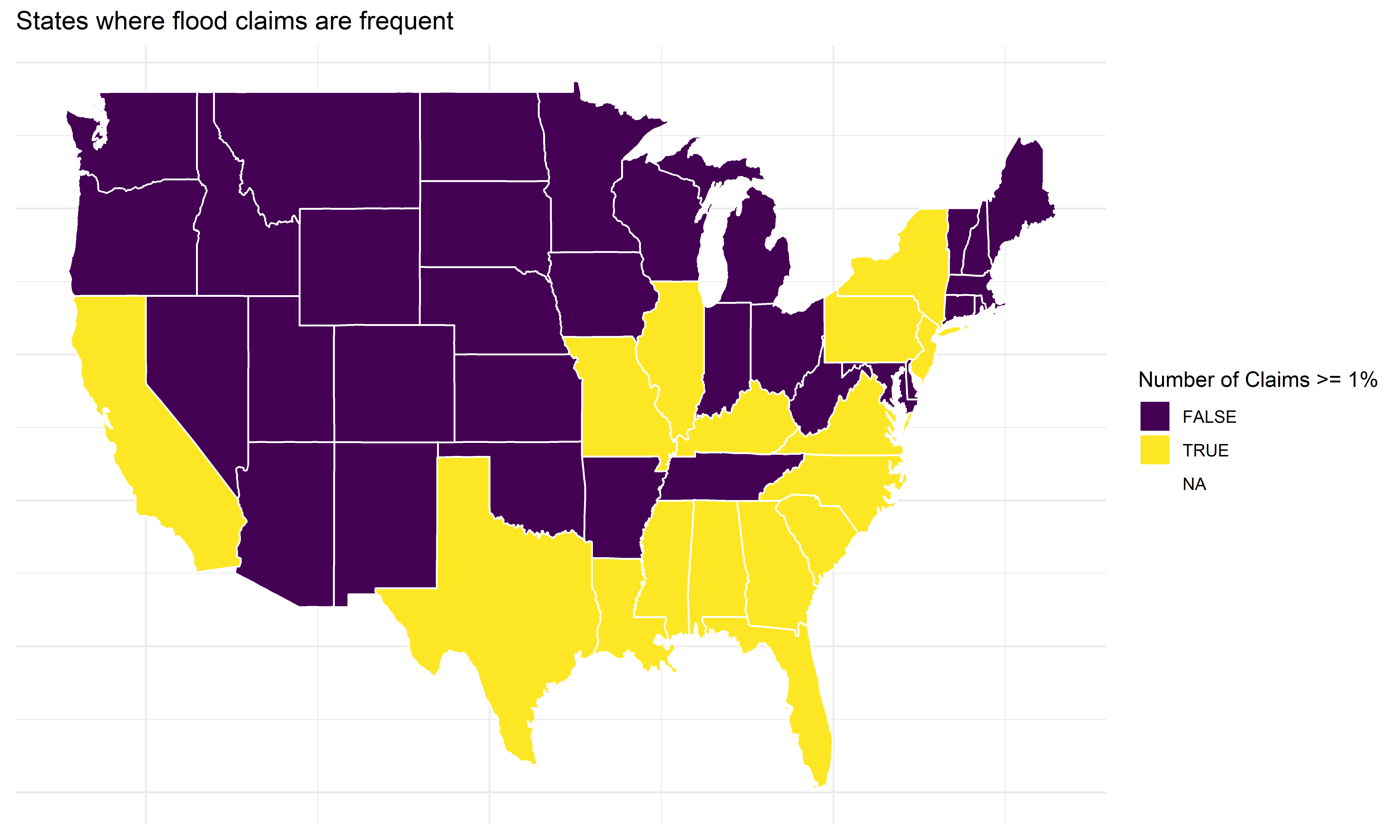
Geographical distribution of perils
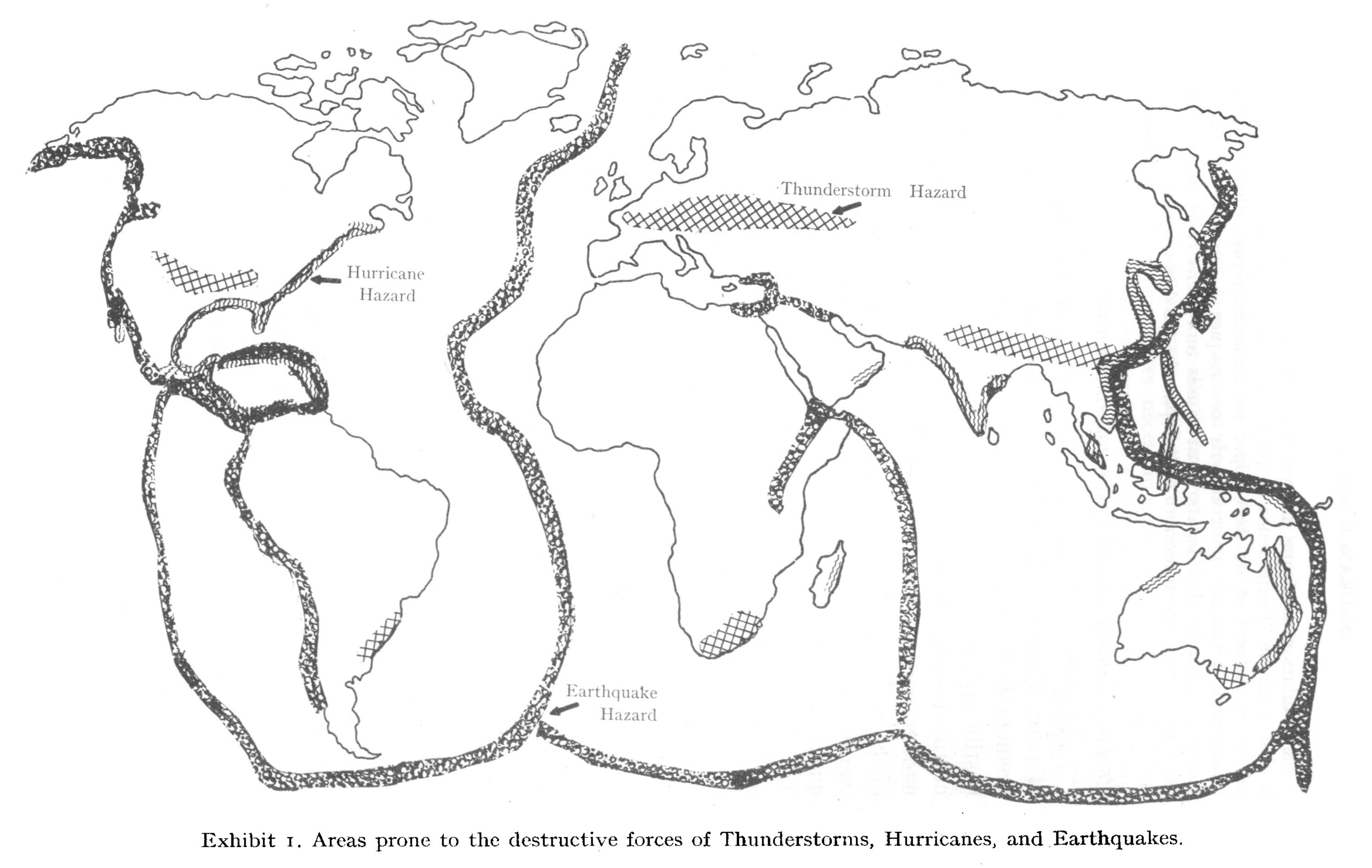
Friedman Exhibit 1 (p. 10).
Source: Friedman, D. G. (1972), Insurance and the natural hazards. ASTIN Bulletin: The Journal of the IAA, 7(1), 4-58.
Hot spots
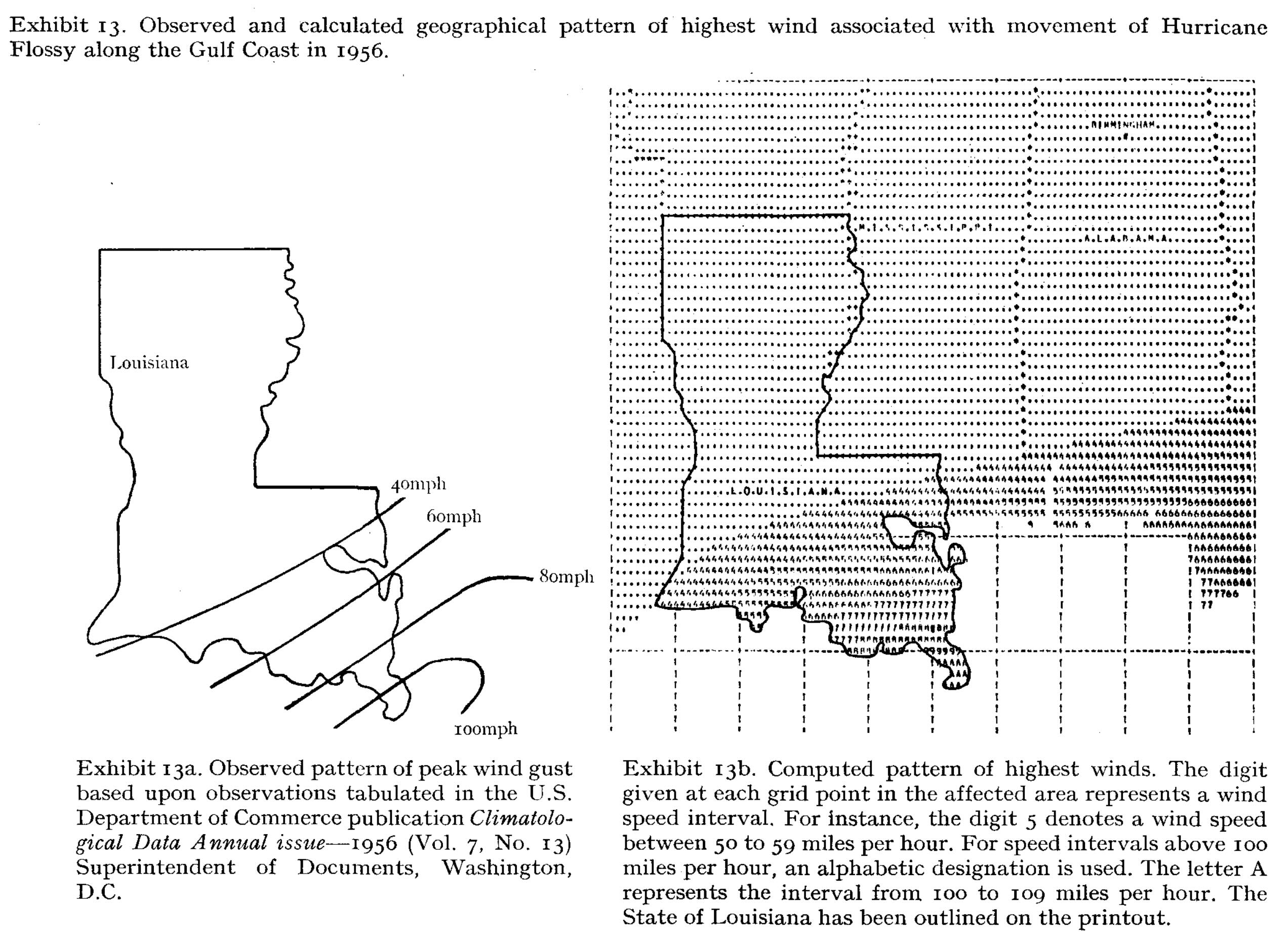
Friedman Exhibit 13 (p. 46).
Source: Friedman, D. G. (1972), Insurance and the natural hazards. ASTIN Bulletin: The Journal of the IAA, 7(1), 4-58.
Reduce the number of levels
AK AL AR AZ CA CO CT DC DE FL GA GU HI
27 2019 410 139 1408 191 819 10 303 11833 1035 6 152
IA ID IL IN KS KY LA MA MD ME MI MN MO
504 43 1605 662 241 1012 20785 885 696 115 402 368 1752
MS MT NC ND NE NH NJ NM NV NY OH OK OR
2753 53 5023 513 189 142 8520 48 81 5899 790 490 237
PA PR RI SC SD TN TX UN UT VA VI VT WA
2363 569 238 2023 136 809 17759 10 11 2006 83 108 522
WI WV WY
313 874 16 [1] 55# States with fewer than 1% claims
rare_flood_states <- names(which(table(claims[["state"]]) < nrow(claims) / 100))
claims$state <- ifelse(claims$state %in% rare_flood_states, "Other", claims$state)
table(claims$state)
AL CA FL GA IL KY LA MO MS NC NJ NY Other
2019 1408 11833 1035 1605 1012 20785 1752 2753 5023 8520 5899 12205
PA SC TX VA
2363 2023 17759 2006 [1] 17New tree
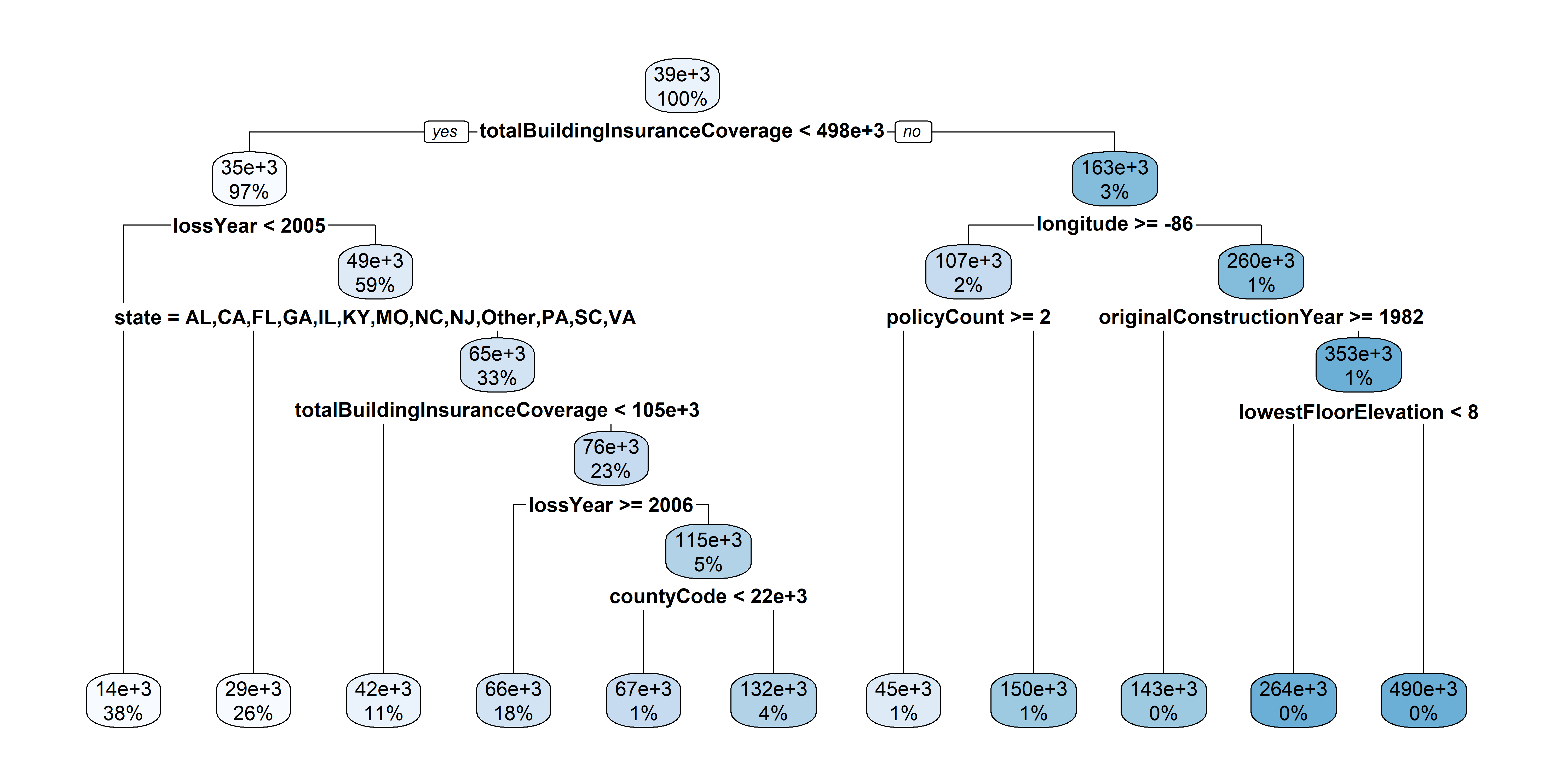
More data
Pruning a Tree
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
What’s the best size of tree
The smallest tree is just a root node (no splits).
The upper limit is to grow until one observation in each region.
How large should we grow the tree?
- What’s wrong if the tree is too small?
- What’s wrong if the tree is too large?

A large tree for the flood insurance data
Code
# I have already shuffled this data
train_val_index <- 1:(0.8*nrow(claims))
train_val_set <- claims[train_val_index, ]
test_set <- claims[-train_val_index, ]
train_index <- 1:(0.75*nrow(train_val_set))
train_set <- train_val_set[train_index, ]
val_set <- train_val_set[-train_index, ]
# train_set$rateMethod <- factor(train_set$rateMethod)
train_set$state <- factor(train_set$state)
# val_set$rateMethod <- factor(val_set$rateMethod, levels = levels(train_set$rateMethod))
val_set$state <- factor(val_set$state, levels = levels(train_set$state))
# test_set$rateMethod <- factor(test_set$rateMethod, levels = levels(train_set$rateMethod))
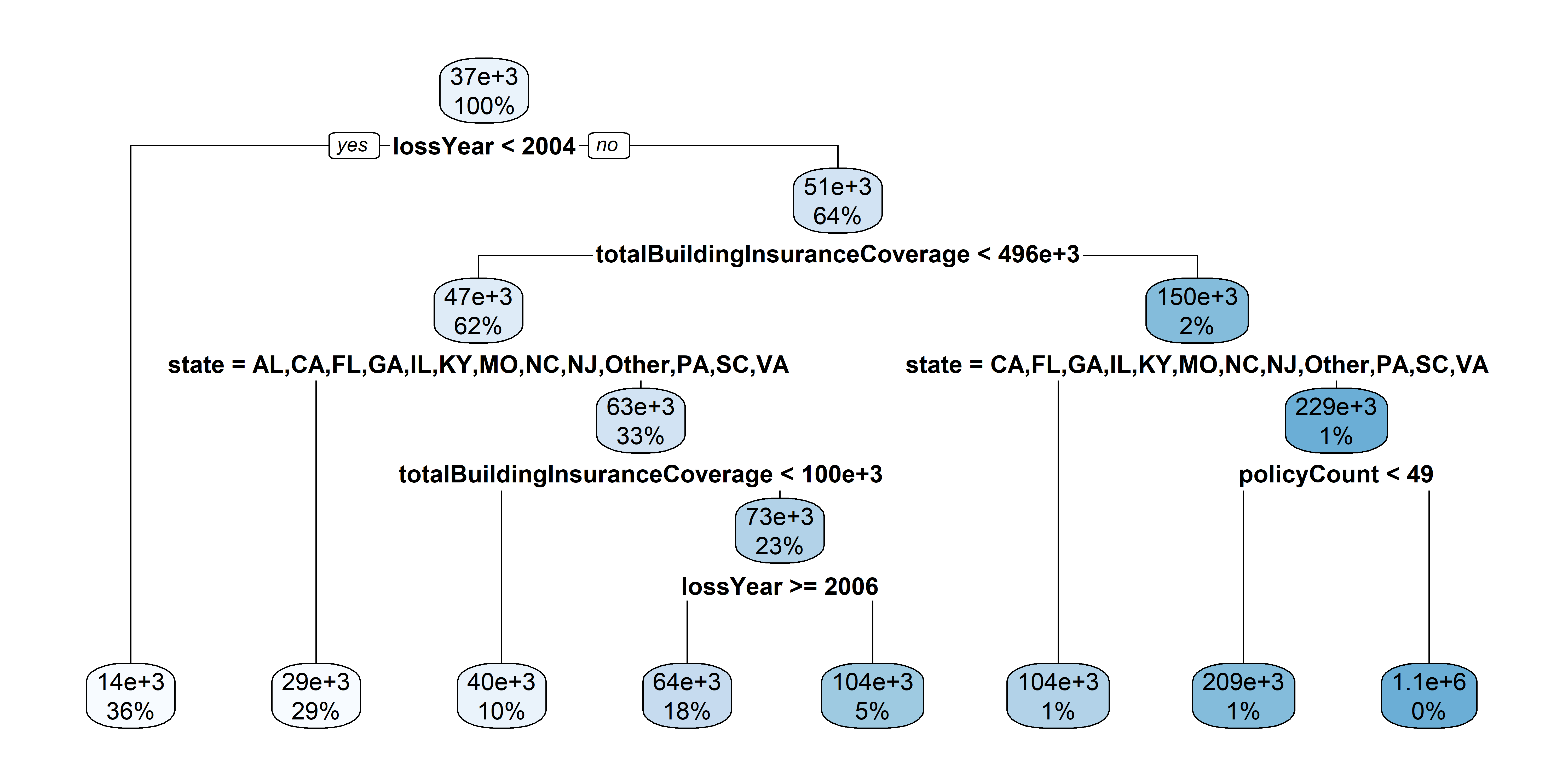
test_set$state <- factor(test_set$state, levels = levels(train_set$state))
The full tree for train pricing
Early stopping of training
“In order to reduce the size of the tree and hence to prevent overfitting, these stopping criteria that are inherent to the recursive partitioning procedure are complemented with several rules. Three stopping rules that are commonly used can be formulated as follows:
- A node t is declared terminal when it contains less than a fixed number of observations.
- A node t is declared terminal if at least one of its children nodes t_L and t_R that results from the optimal split s_t contains less than a fixed number of observations.
- A node t is declared terminal when its depth is equal to a fixed maximal depth.”
Source: Denuit et al. (2020), Effective Statistical Learning Methods for Actuaries II: Tree-Based Methods and Extensions, Springer, p. 58.
Pruning motivation
“While the stopping rules presented above may give good results in practice, the strategy of stopping early the growing of the tree is in general unsatisfactory… That is why it is preferable to prune the tree instead of stopping the growing of the tree. Pruning a tree consists in fully developing the tree and then prune it upward until the optimal tree is found.”
- A decision rule of considering the decrease in RSS at each step/split (versus a threshold) is too short-sighted.
- Alternate approach of growing a large tree then pruning back to obtain a subtree is a better strategy.
- Cross validation of each possible subtree is however very cumbersome.
- An alternative approach is cost complexity pruning (also known as weakest link pruning)
Source: Denuit et al. (2020), Effective Statistical Learning Methods for Actuaries II: Tree-Based Methods and Extensions, Springer, p. 59.
Cost-Complexity Pruning
Define a subtree T \subset T_0 to be any tree than can be obtained by pruning T_0 (a fully-grown tree)
- The mth terminal node (aka “leaf”, aka “region”) is denoted R_m
- |T|: number of terminal nodes in T
Define the cost complexity criterion
\text{Total cost} = \text{Measure of Fit} + \text{Measure of Complexity}
C_\alpha(T) = \sum_{m=1}^{|T|} \sum_{i \in R_m} (y_i - \hat{y}_m)^2 + \alpha|T| where \hat{y}_m is the mean y_i in the mth leaf and \alpha controls the tradeoff between tree size and goodness of fit.
Cost-Complexity Pruning
- For each specific \alpha, we must find the subtree T_\alpha \subset T_0 that minimises C_\alpha(T).
- It turns out that it is not too computationally expensive to find T_{\alpha} for a sequence of increasing \alpha’s, because “branches get pruned from the tree in a nested and predictable fashion” (James et al., 2021).
- This is called “cost-complexity pruning” or “weakest link pruning”.
- But how do we choose \alpha (and hence the final “optimally pruned” tree)?
- cross-validation!
Pruning a Tree: Algorithm Summary
- Use recursive binary splitting to grow a large tree on the training data
- stop only when each terminal node has fewer than some minimum number of observations
- Apply cost complexity pruning to the large tree to obtain a sequence of best subtrees, as a function of \alpha
- there is a unique subtree T_\alpha that minimises C_\alpha(T)
- Use K-fold cross-validation to choose \alpha
- Return the subtree from Step 2 that corresponds to the chosen value of \alpha
CV to prune Hitters tree (only 2 predictors)
- For our
Hittersexample, a tree with 3 or 4 leaves (equivalently, 2 and 3 splits) is probably best.
CP nsplit rel error xerror xstd
1 0.44457445 0 1.0000000 1.0072170 0.06567495
2 0.11454550 1 0.5554255 0.5640321 0.05904335
3 0.04446021 2 0.4408800 0.4620370 0.05746429
4 0.01831268 3 0.3964198 0.4290060 0.05941502
5 0.01690198 4 0.3781072 0.4329760 0.06391180
6 0.01107214 5 0.3612052 0.4329270 0.06603000
7 0.01000000 6 0.3501330 0.4445006 0.06621925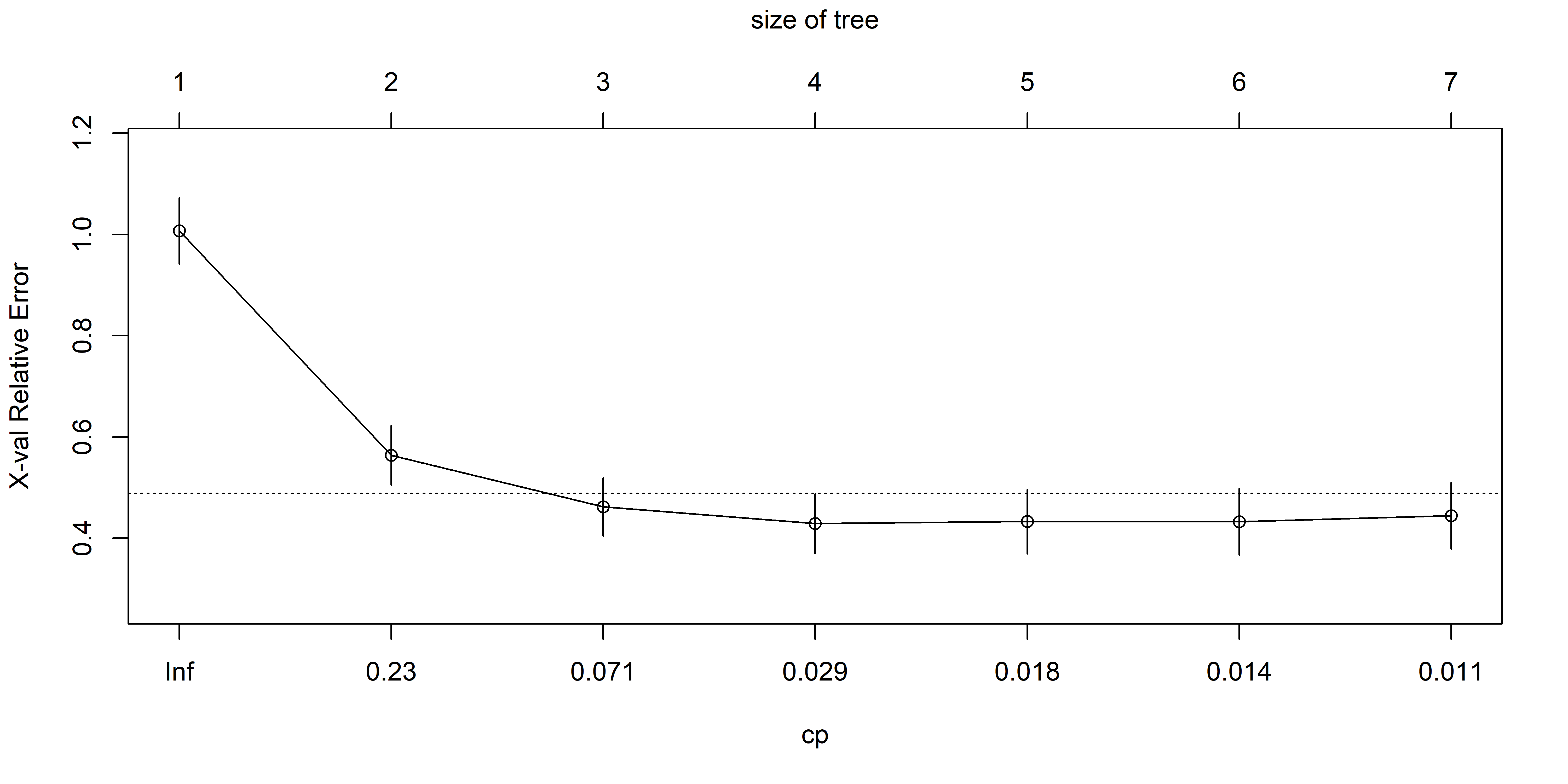
Unpruned Hitters tree: all predictors
The unpruned tree that results from top-down greedy splitting on the training data.
Source: James et al. (2021), An Introduction to Statistical Learning, Figure 8.4.
CV to pick \alpha (equiv., |T|)
The training, cross-validation, and test MSE are shown as a function of the number of terminal nodes in the pruned tree. Standard error bands are displayed. The minimum cross-validation error occurs at a tree of size three.
Source: James et al. (2021), An Introduction to Statistical Learning, Figure 8.5.
CV to prune NFIP tree
Cross-validation to prune the large NFIP tree
# Perform cross-validation to prune the tree
set.seed(123)
cv_tree <- train(
amountPaidOnBuildingClaim ~ .,
data=train_set,
method="rpart",
trControl=trainControl(method="cv", number=5),
tuneGrid=data.frame(cp=seq(0, 0.01, 0.001))
)
# Get the optimal cp value
optimal_cp <- cv_tree$bestTune$cp
plot(cv_tree)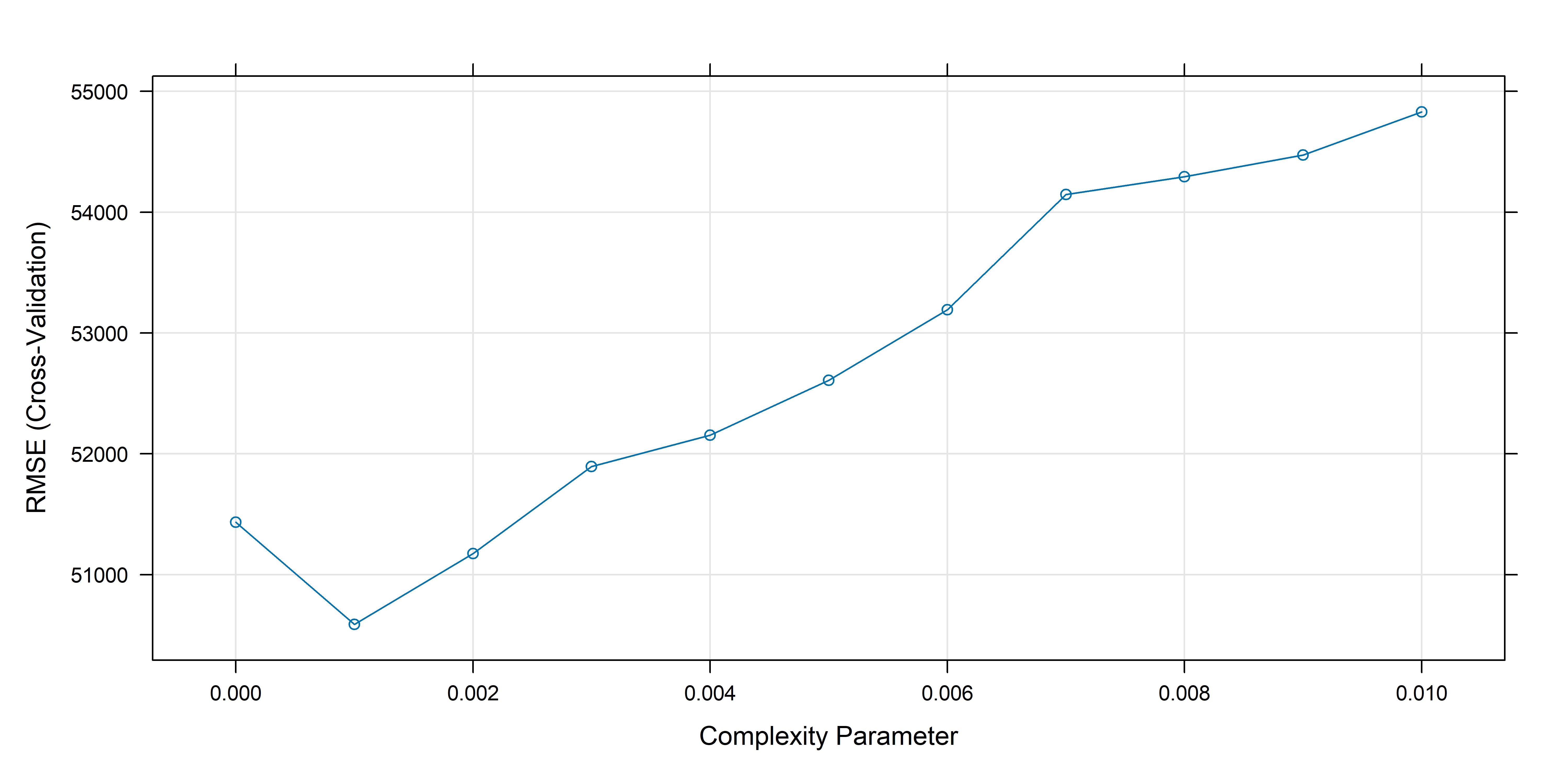
The pruned tree
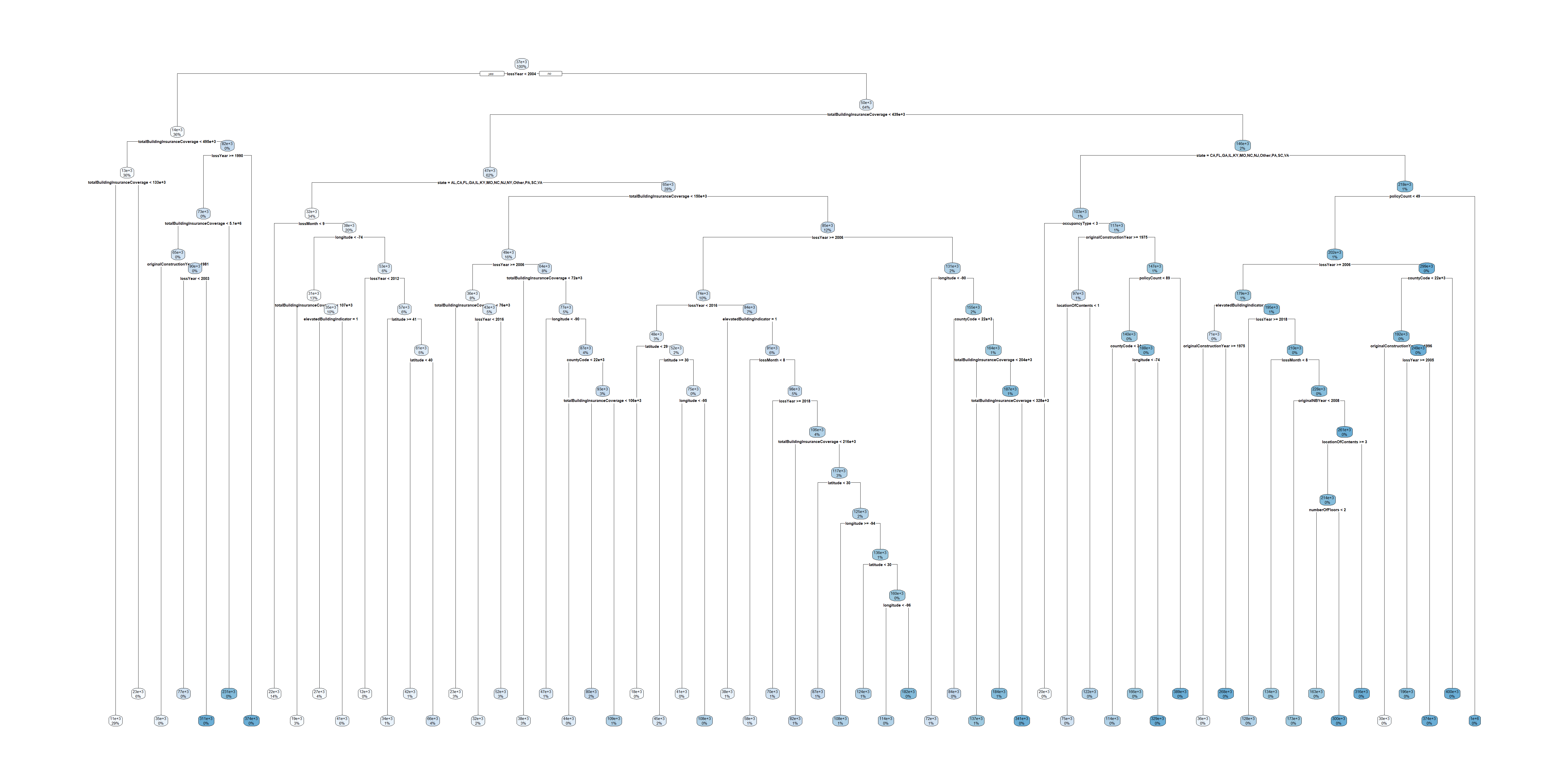
Linear model
Call:
lm(formula = amountPaidOnBuildingClaim ~ ., data = train_set)
Residuals:
Min 1Q Median 3Q Max
-785390 -27448 -10894 11246 4787232
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.793e+06 6.662e+04 -41.928 < 2e-16 ***
agricultureStructureIndicator 1.662e+04 1.669e+04 0.996 0.319163
policyCount 1.463e+03 1.179e+02 12.407 < 2e-16 ***
countyCode 6.958e-02 3.986e-02 1.746 0.080900 .
elevatedBuildingIndicator -1.387e+04 6.202e+02 -22.358 < 2e-16 ***
latitude 3.955e+02 1.031e+02 3.835 0.000125 ***
locationOfContents 4.392e+02 1.412e+02 3.111 0.001864 **
longitude -1.455e+02 3.953e+01 -3.681 0.000232 ***
lowestFloorElevation -4.797e-02 5.281e-01 -0.091 0.927623
occupancyType 3.937e+03 1.681e+02 23.413 < 2e-16 ***
postFIRMConstructionIndicator 3.291e+03 7.311e+02 4.501 6.78e-06 ***
stateCA -8.250e+03 2.975e+03 -2.773 0.005548 **
stateFL -1.210e+04 1.873e+03 -6.459 1.07e-10 ***
stateGA -1.194e+04 2.955e+03 -4.040 5.36e-05 ***
stateIL -2.142e+04 2.859e+03 -7.494 6.80e-14 ***
stateKY -1.385e+04 3.145e+03 -4.405 1.06e-05 ***
stateLA 1.495e+04 1.944e+03 7.688 1.52e-14 ***
stateMO -1.212e+04 2.888e+03 -4.198 2.70e-05 ***
stateMS 2.054e+04 2.442e+03 8.410 < 2e-16 ***
stateNC -1.536e+04 2.588e+03 -5.935 2.95e-09 ***
stateNJ -9.051e+03 2.700e+03 -3.353 0.000801 ***
stateNY -4.034e+03 2.869e+03 -1.406 0.159733
stateOther -1.757e+04 2.507e+03 -7.006 2.48e-12 ***
statePA -1.705e+04 3.180e+03 -5.360 8.37e-08 ***
stateSC -1.064e+04 2.999e+03 -3.549 0.000387 ***
stateTX 4.916e+03 2.589e+03 1.898 0.057665 .
stateVA -2.123e+04 3.337e+03 -6.363 1.99e-10 ***
totalBuildingInsuranceCoverage -1.912e-03 6.089e-04 -3.140 0.001693 **
numberOfFloors -5.613e+01 3.050e+02 -0.184 0.854001
lossYear 1.400e+03 4.691e+01 29.845 < 2e-16 ***
lossMonth 2.253e+03 1.018e+02 22.130 < 2e-16 ***
originalConstructionYear 5.103e+00 2.298e+01 0.222 0.824242
originalConstructionMonth -8.065e+01 7.097e+01 -1.136 0.255851
originalNBYear -1.772e+01 4.758e+01 -0.372 0.709551
originalNBMonth 1.601e+01 7.470e+01 0.214 0.830288
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 57740 on 59965 degrees of freedom
Multiple R-squared: 0.1328, Adjusted R-squared: 0.1323
F-statistic: 270 on 34 and 59965 DF, p-value: < 2.2e-16Comparing models
| Method | Test RMSE |
|---|---|
| Linear Model | 5.4792^{4} |
| Large Tree | 4.8683^{4} |
| Pruned Tree | 4.7372^{4} |
Bootstrap Aggregation
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
Advantages and disadvantages of trees
Advantages
- Easy to explain
- (Mirror human decision making)
- Graphical display
- Easily handle qualitative predictors
Disadvantages
- Low predictive accuracy compared to other regression and classification approaches
- Can be very non-robust
Is there a way to improve the predictive performance of trees?
- Pruning a decision tree
- Ensemble methods
- Bootstrap aggregation (bagging)
- Random forest
- Boosting
An ensemble is a group of models…
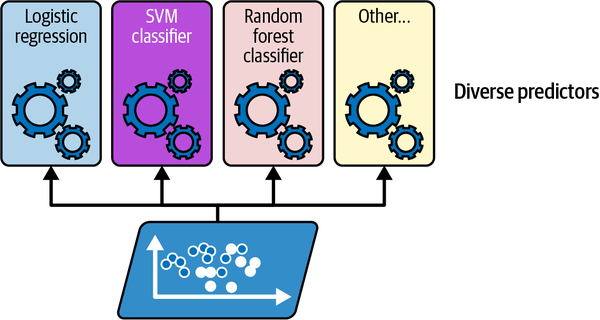
Training various different classifiers on the same dataset.
Source: Geron (2022), Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd ed., Figure 7-1.
… & you combine their predictions
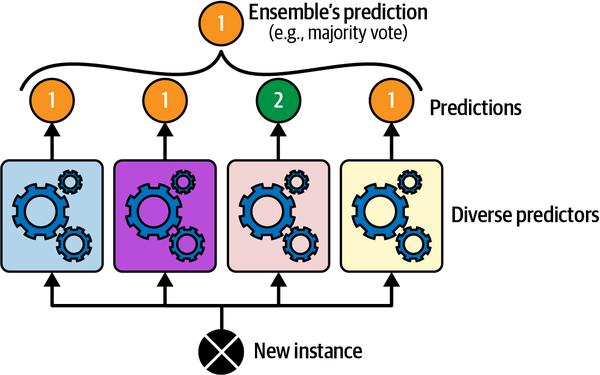
Make an overall prediction based on the majority vote of the models.
Source: Geron (2022), Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd ed., Figure 7-2.
Bootstrapping
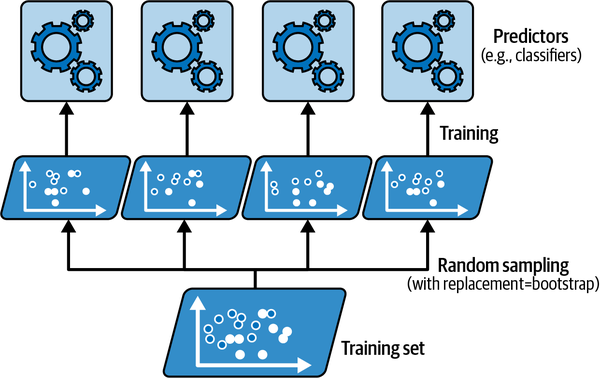
Train on different versions of the same data.
Source: Geron (2022), Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd ed., Figure 7-4.
Bootstrap resampling I
Original dataset
There are 54% of the rows in the original dataset in the bootstrap resample.
Bootstrap resampling II
Original dataset
There are 68% of the rows in the original dataset in the bootstrap resample.
Bootstrap Aggregation (Bagging)
- A general-purpose procedure to reduce the variance of predictions; but particularly useful (and frequently used) in the context of decision trees.
Bagging procedure for trees:
- Bootstrap: re-sample (with replacement) the original data set repeatedly, hence obtain B different bootstrapped training data sets
- Train: train a tree on the bth bootstrapped training set (no need to prune), hence obtain the model \hat{f}^{\ast b}(x)
- Aggregate: for regression, take the average prediction, at any point x: \hat{f}_\text{bag}(x) = \dfrac{1}{B}\sum_{b=1}^{B} \hat{f}^{\ast b}(x) (same idea for classification, but take a “majority vote”, i.e., for any given x, choose the most common category predicted for that x by the B models)
Bagging: Illustration
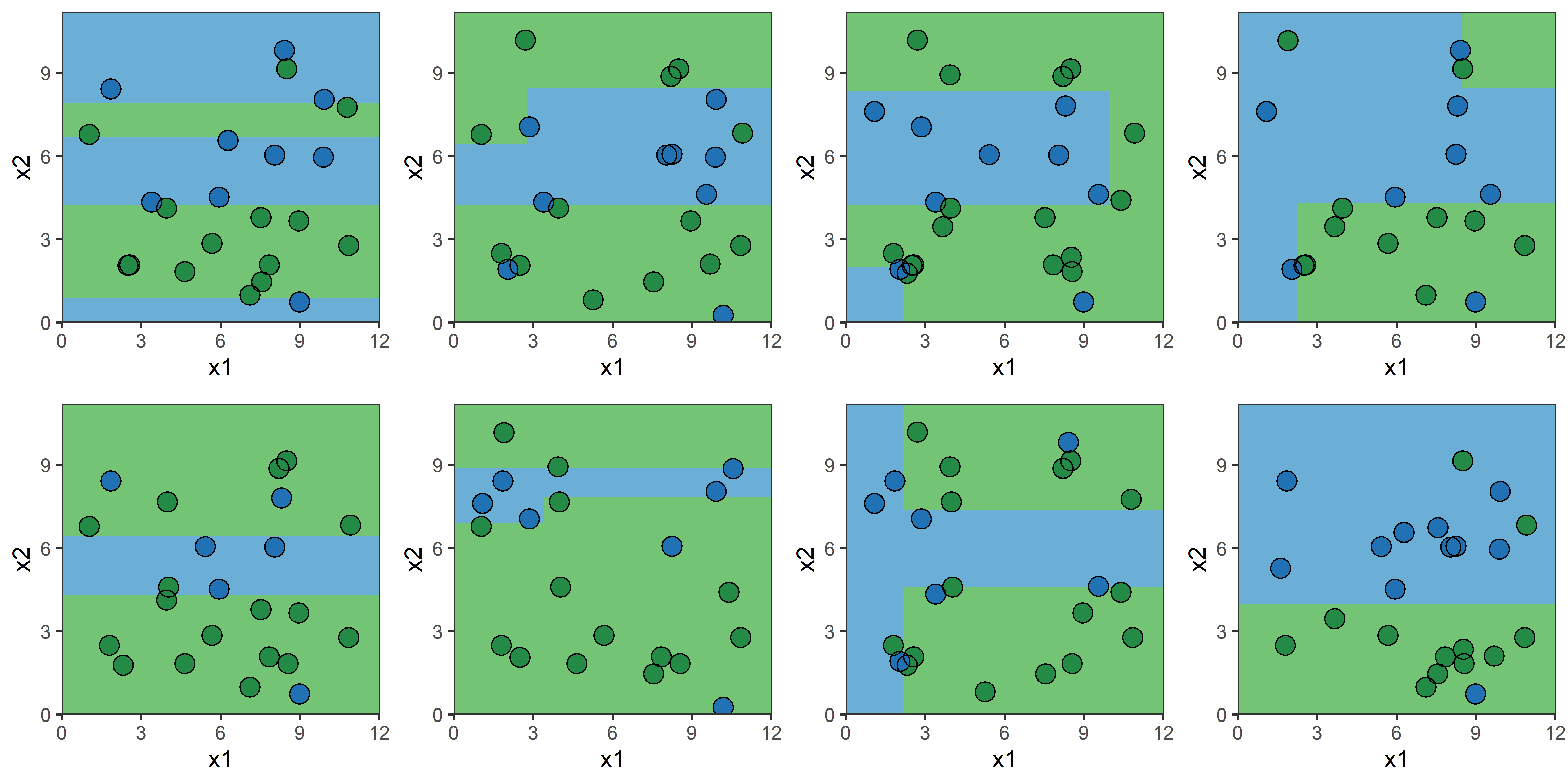
Bagging: Illustration
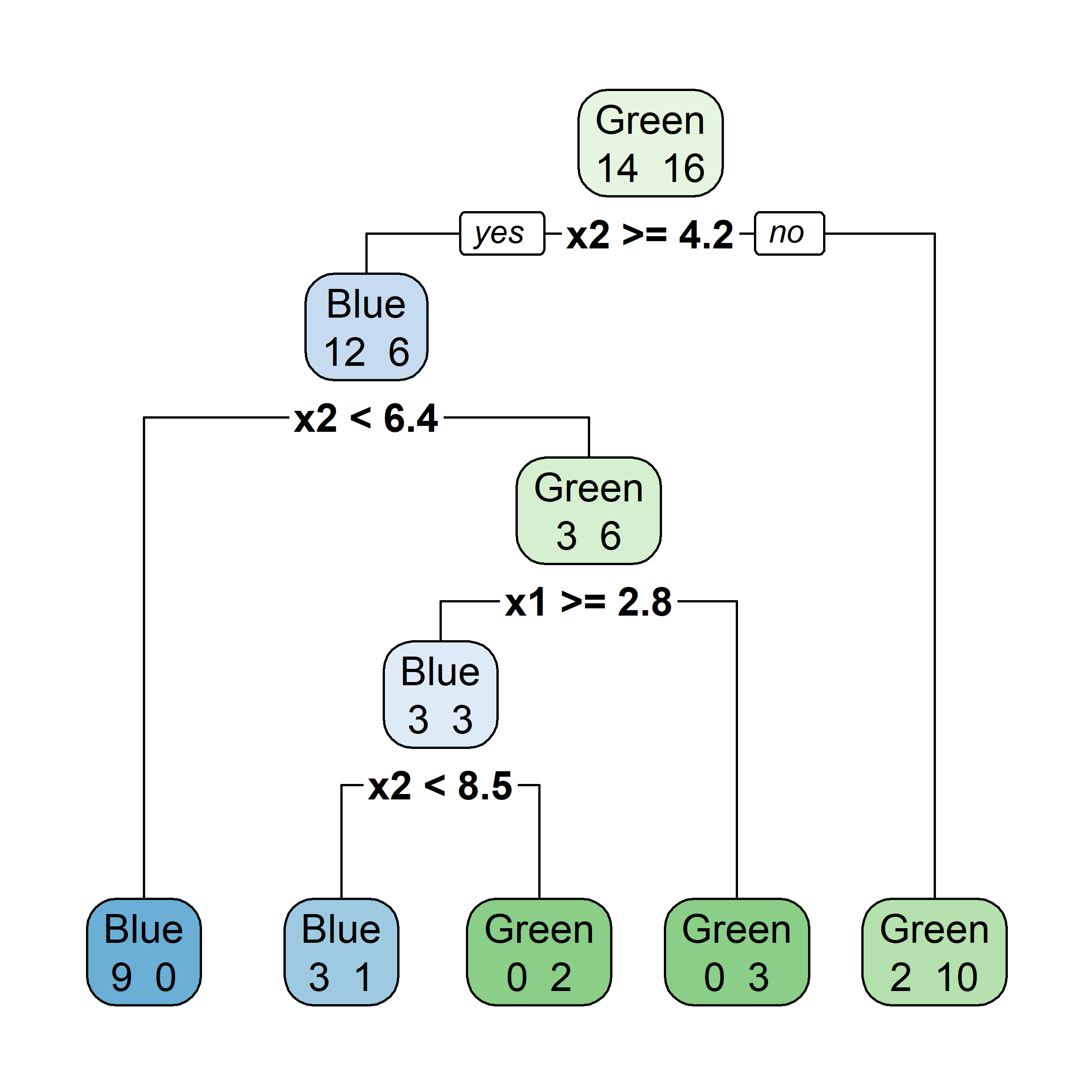
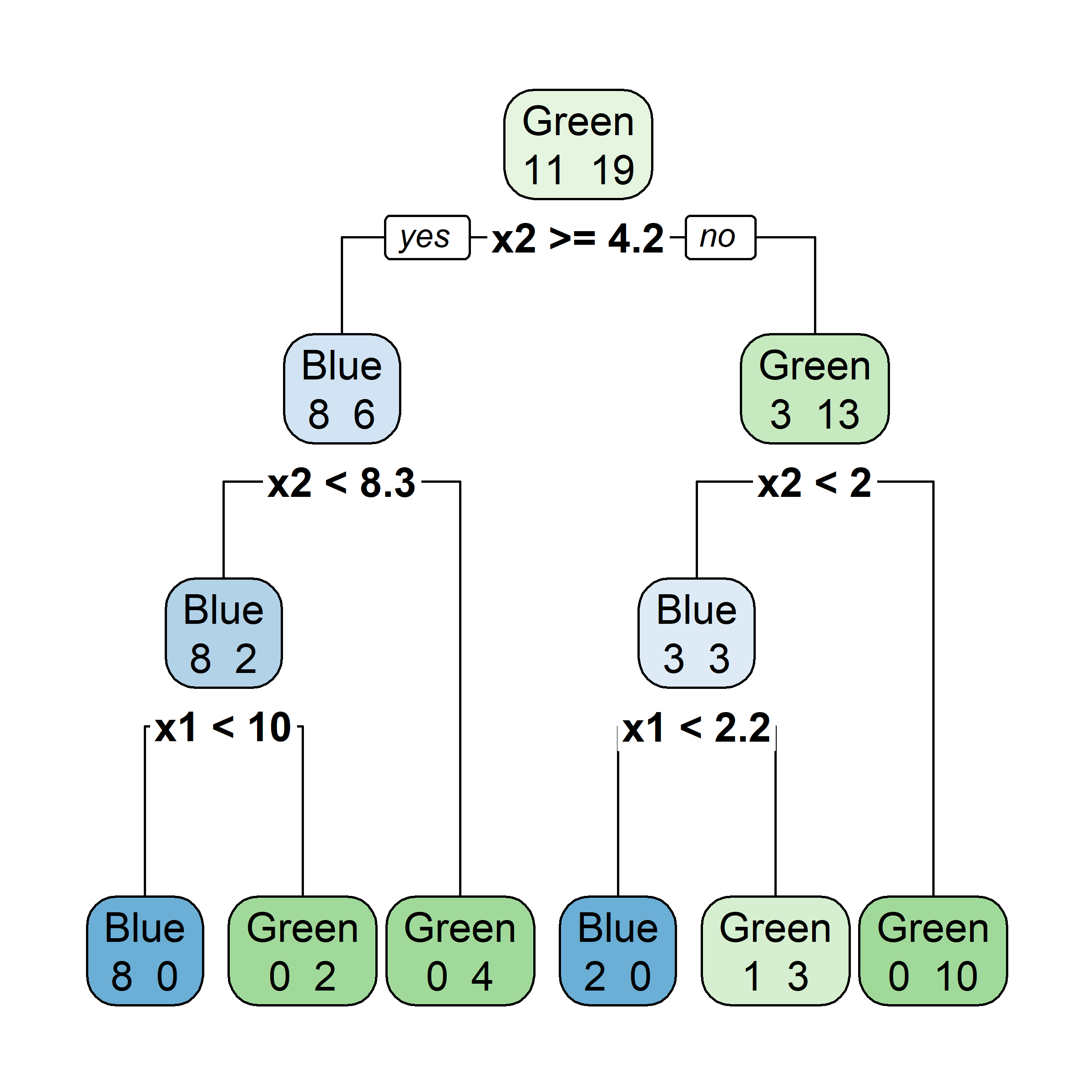
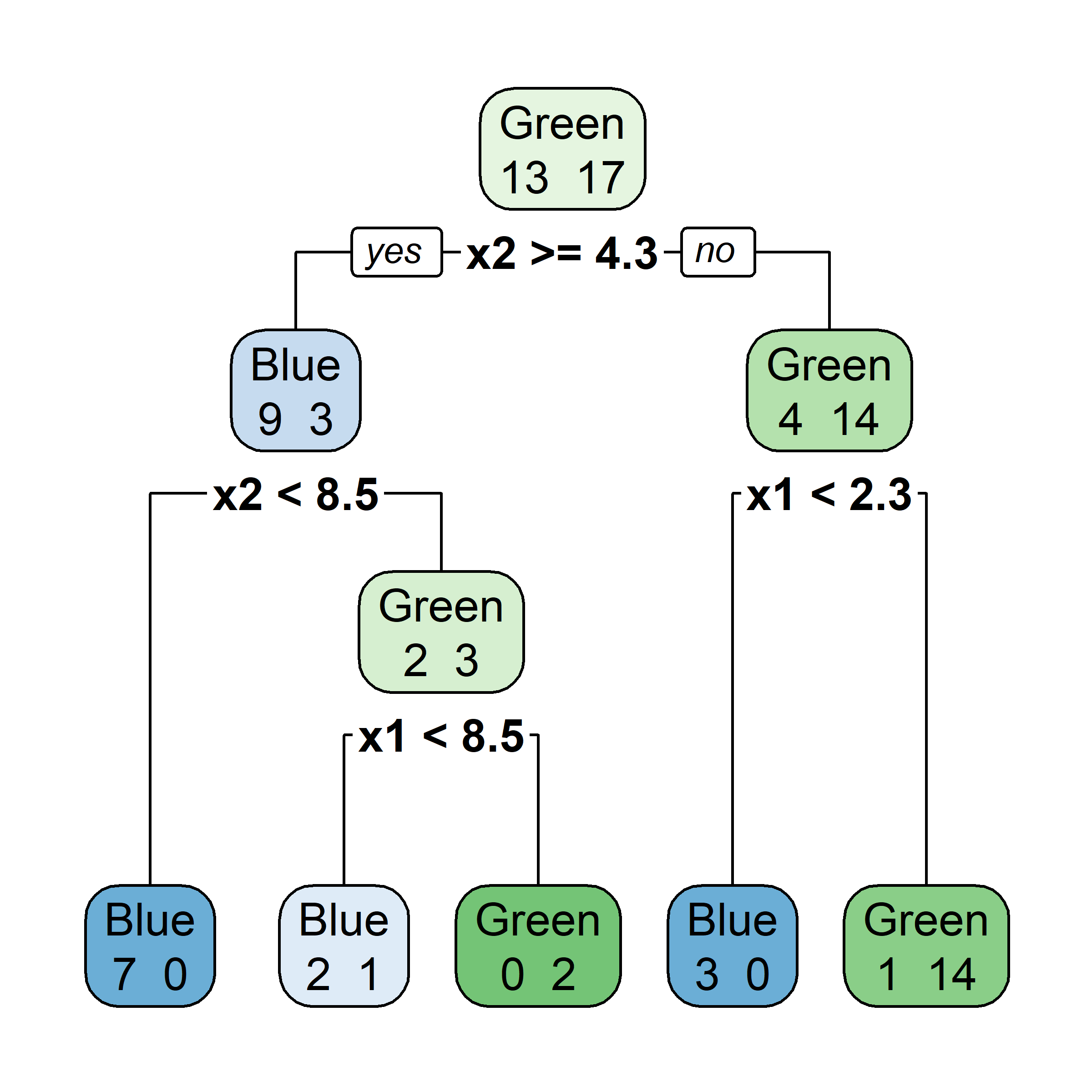
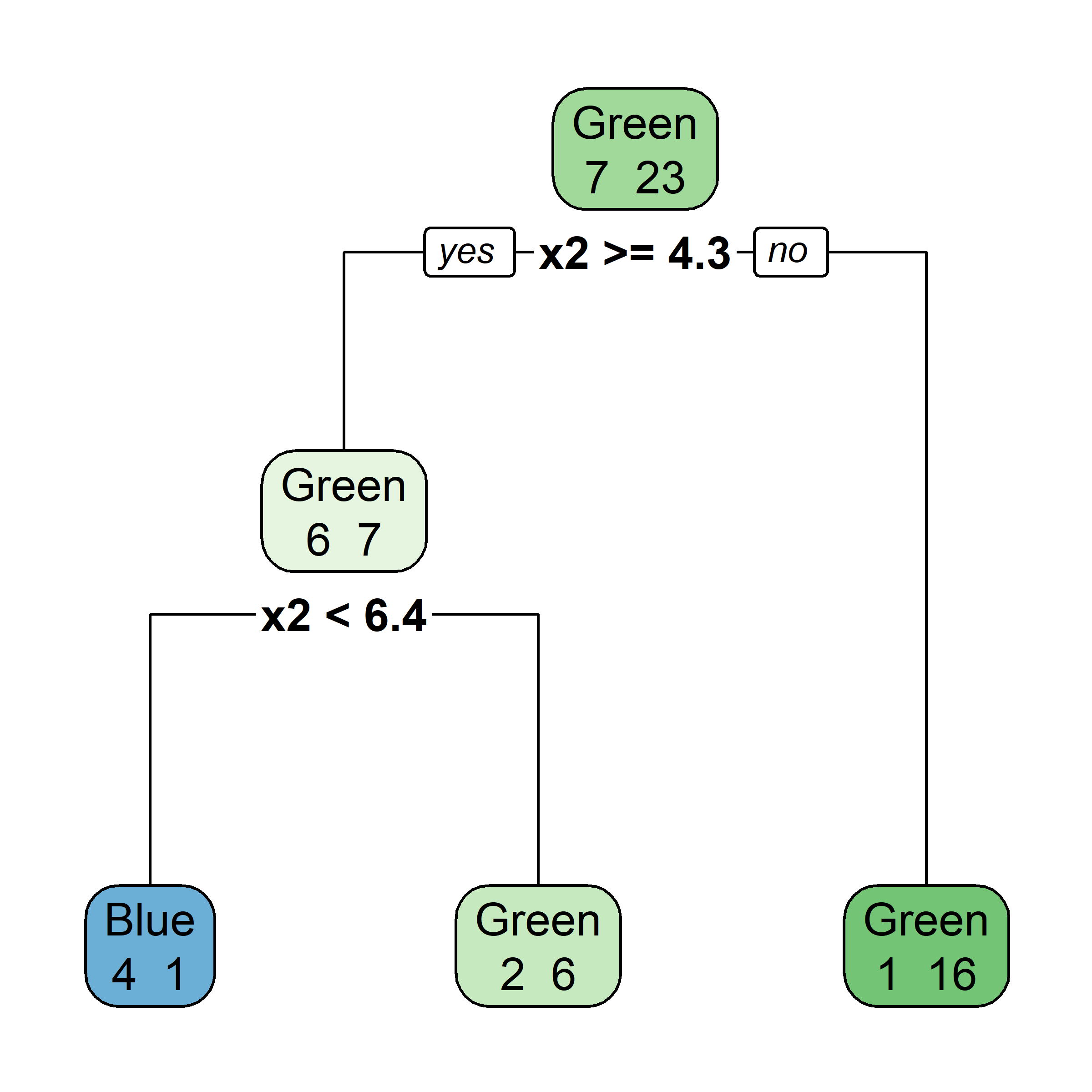
Samples that are in the bag
Let’s say element i,j of the matrix is 1 if the ith observation is in the jth bootstrap sample (we say it is “in the bag”) and 0 otherwise.
Samples that are out of bag
Now consider the inverse, element i,j of the matrix is 1 if the ith observation is not in the jth bootstrap sample, it is “out of the bag”.
This provides a simple way to estimate the test error of the bagged model: “out-of-bag error” (cheaper than cross-validation).
Out-of-bag error estimation
There is a very straightforward way to estimate the test error of a bagged model
- On average, each bagged tree makes use of around two-thirds of the observations.
- The remaining observations (one-third, on average) are referred to as the out-of-bag (OOB) observations.
- Predict the response for the ith observation using each of the trees for which that observation was OOB
- \sim B/3 predictions for the ith observation
- Take the average (regression) or majority (classification) prediction to obtain the final OOB prediction for the ith observation.
- “with B sufficiently large, OOB error is virtually equivalent to leave-one-out cross-validation error” (James et al., 2021).
Bagging: variable selection
- Bagging can lead to difficult-to-interpret results, as we don’t get a single tree (but a large number of them, each of which may use different predictors and have different leaves).
- Still, a predictor’s overall “importance” can be measured
- Bagging regression trees: “we can record the total amount that the RSS (8.1) is decreased due to splits over a given predictor, averaged over all B trees” (James et al., 2021).
- Bagging classification trees: “we can add up the total amount that the Gini index (8.6) is decreased by splits over a given predictor, averaged over all B trees” (James et al., 2021).
Random Forests
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
Random Forests

This is a forest (stock photo)
Random Forests in a nutshell
- An issue with bagging is that it tends to produce very correlated trees.
- Random forests are an alternative that produces “less correlated” trees.
- In random forests, we build trees under an important restriction: whenever a new “split” is created, it is only allowed to use one out of m (randomly selected) predictors.
- For each new split, a new random set of m predictors (out of the total p) is considered.
- An effect this has is that “strong” predictors are used in (far) fewer models, and hence the other predictors have the opportunity to have their effects captured by more trees (the smaller guys also get their chance to shine!).
- Random forests tend to reduce the variance of the final predictions (at the cost of introducing some bias).
- Typically, we choose m \approx \sqrt{p}.
- Bagging can be said to be a special case of random forests, with m=p.
Fitting with package randomForest
| Method | RMSE |
|---|---|
| Linear Model | 5.4792^{4} |
| Large Tree | 4.8683^{4} |
| Pruned Tree | 4.7372^{4} |
| Random Forest | 4.2829^{4} |
Variable importance
%IncMSE IncNodePurity
agricultureStructureIndicator -0.4092969 7.736630e+10
policyCount -0.6649637 1.312233e+13
countyCode 7.0676498 1.261540e+13
elevatedBuildingIndicator 1.9163476 4.066224e+12
latitude 12.7351805 1.257793e+13
locationOfContents 1.2897842 5.107086e+12
longitude 15.2725053 1.588849e+13
lowestFloorElevation 0.5264056 8.837304e+12
occupancyType -0.8955214 5.325440e+12
postFIRMConstructionIndicator 12.1436127 1.855385e+12
state 10.2933401 1.275269e+13
totalBuildingInsuranceCoverage 8.0324394 4.040641e+13
numberOfFloors 11.7156439 3.504747e+12
lossYear 8.2085826 2.277261e+13
lossMonth 17.4917355 1.009505e+13
originalConstructionYear 9.4747850 1.235049e+13
originalConstructionMonth 2.8065239 6.062158e+12
originalNBYear 6.7318799 1.468756e+13
originalNBMonth 1.5024842 1.277571e+13Variable importance plot

Boosting
Lecture Outline
Decision Trees
Growing a Tree
National Flood Insurance Program Demo
Pruning a Tree
Bootstrap Aggregation
Random Forests
Boosting
Boosting
- A general approach that can be applied to many statistical learning methods for regression or classification.
- We focus on boosting for regression trees.
- It also combines a large number of decision trees, but
- it does not rely on independent bootstrap samples
- instead, trees are grown sequentially: each new tree is created using information from previously grown trees
- each tree is fitted on a modified version of the original data, namely updated residuals from the previous tree model
- By fitting residuals, at each step this method specifically targets areas where the previous tree did not perform well.
- Unlike for standard trees, boosting enforces slow learning.
Boosting Algorithm for Regression Trees
- Set \hat{f}(x)=0 and r_i = y_i for all i in the training set.
- For b = 1, 2, \cdots, B, repeat:
- Fit a tree \hat{f}^b with d splits (d+1 terminal nodes) to the training data (X, r).
- Update \hat{f} by adding in a shrunken version of the new tree \hat{f}(x) \leftarrow \hat{f}(x) + \lambda \hat{f}^b(x)
- Update the residuals, r_i \leftarrow r_i - \lambda \hat{f}^b(x_i)
- After the a)-b)-c) steps in 2 have been performed B times, the final boosted model is simply the last iteration of \hat{f}(x).
Note: the final model can be expressed as: \hat{f}(x) = \sum_{b=1}^{B}\lambda \hat{f}^b(x).
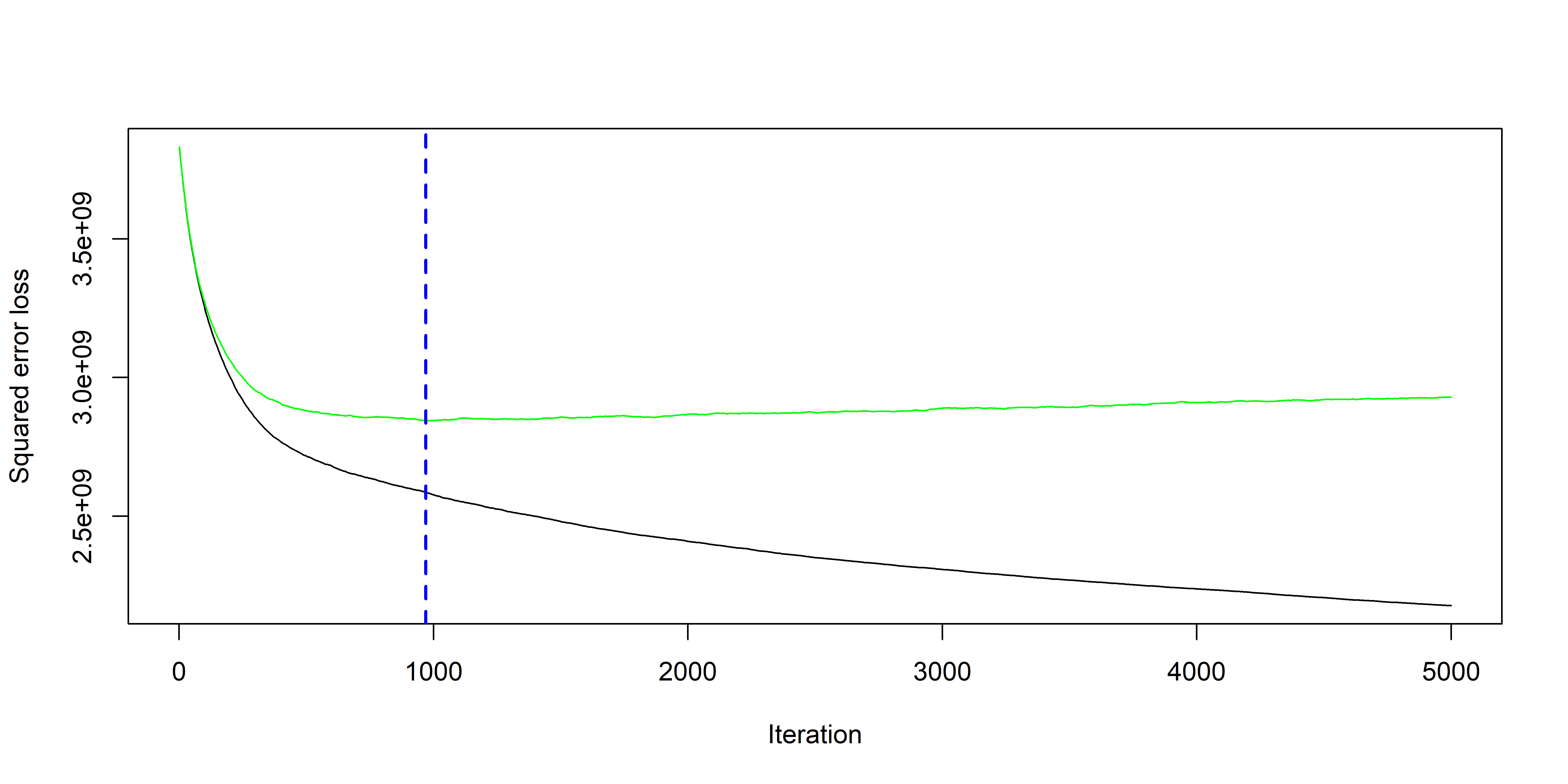
Boosting Tuning Parameters
- The number of trees B
- danger to overfit if B is too large
- use cross-validation to select B
- The shrinkage parameter \lambda
- a small positive number
- controls the rate at which boosting learns
- typical values are 0.01 or 0.001
- The number d of splits in each tree
- d=1 often works well, each tree is a “stump”
Fitting with package gbm
Comparing models
| Method | RMSE |
|---|---|
| Linear Model | 5.4792^{4} |
| Gradient Boosting | 4.982^{4} |
| Large Tree | 4.8683^{4} |
| Pruned Tree | 4.7372^{4} |
| Random Forest | 4.2829^{4} |
Finally, evaluating the winning model on the test set:
if (val_rmse_gbm < val_rmse_rf) {
predictions <- predict(gbm_model, newdata = test_set, n.trees = best_iter)
test_rmse <- sqrt(mean((predictions - test_set$amountPaidOnBuildingClaim)^2))
} else {
predictions <- predict(rf_model, newdata = test_set)
test_rmse <- sqrt(mean((predictions - test_set$amountPaidOnBuildingClaim)^2))
}
round(test_rmse)[1] 44468Test set root mean-squared error for the winning model is 4.4468495^{4}.
Boosting (iteration 1)
Code
x_obs = np.linspace(-3, 3, 50)
y_obs = [5, 4, 5, 4, 5, 4, 1, 2, 4, 4, 2, 1, 2, 1, 1, 1, 2, 0, 0, 0, 2, 0, 1, 1, 1, 0, 1, 1, -1, 1, 0, 1, 0, -1, 2, 0, 1, 2, 1, 1, 3, 2, 4, 1, 2, 2, 4, 3, 5, 3]
df = pd.DataFrame({'x': x_obs, 'y': y_obs})
# Parameters
d = 1 # number of splits
lambda_ = 0.5 # learning rate
# Higher resolution grid
x_obs = x_obs.reshape(-1, 1)
x_grid = np.linspace(-3, 3, 1000)
# Initial model
f_hat = np.zeros_like(df['y'], dtype=float)
residuals = df['y'].astype(float).copy()
# Store predictions for the grid
f_hat_grid = np.zeros_like(x_grid, dtype=float)
def plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_):
fig, axes = plt.subplots(1, 3, figsize=(10, 4))
# Plot residuals
axes[0].scatter(df['x'], residuals, color='blue', label='Residuals')
axes[0].plot(x_grid, f_b_grid, color='green', label='New Tree')
axes[0].set_ylim(-1.25, 5.25)
axes[0].set_title(f"Residuals")
# Plot updated model prediction
axes[1].plot(x_grid, f_hat_grid, color='purple')
axes[1].scatter(df['x'], df['y'], color='red', alpha=0.5)
axes[1].set_ylim(-1.25, 5.25)
axes[1].set_title(f"Updated Prediction")
# Plot new residuals
axes[2].scatter(df['x'], df['y'] - f_hat, color='blue', label='Residuals')
axes[2].set_ylim(-1.25, 5.25)
axes[2].set_title(f"New Residuals")
plt.tight_layout()Code
# Fit a tree to residuals
tree = DecisionTreeRegressor(max_depth=d)
tree.fit(x_obs, residuals);
f_b = tree.predict(x_obs)
f_b_grid = tree.predict(x_grid.reshape(-1, 1))
# Update model
f_hat += lambda_ * f_b
f_hat_grid += lambda_ * f_b_grid
plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_)
# Update residuals
residuals -= lambda_ * f_b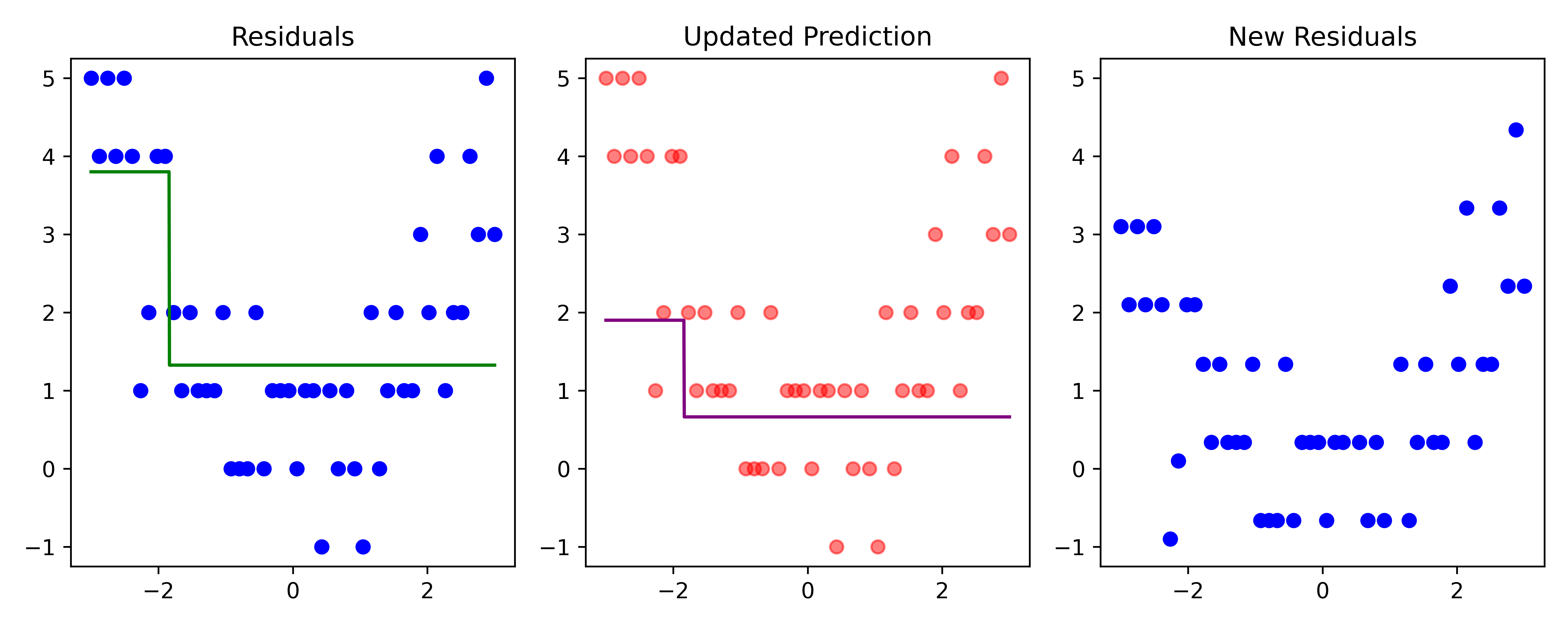
Here, \lambda=\frac12 is the learning rate.
Boosting (iteration 2)
Code
# Fit a tree to residuals
tree = DecisionTreeRegressor(max_depth=d)
tree.fit(x_obs, residuals);
f_b = tree.predict(x_obs)
f_b_grid = tree.predict(x_grid.reshape(-1, 1))
# Update model
f_hat += lambda_ * f_b
f_hat_grid += lambda_ * f_b_grid
plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_)
# Update residuals
residuals -= lambda_ * f_b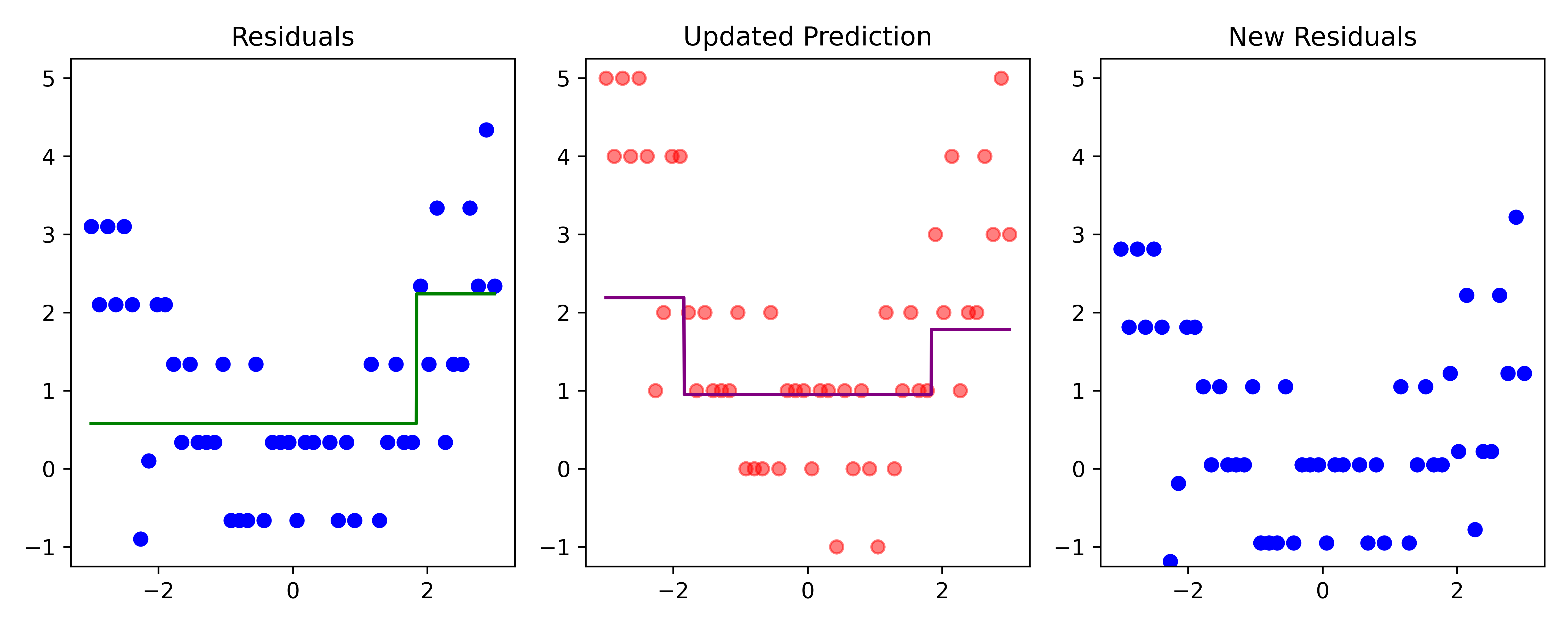
Here, \lambda=\frac12 is the learning rate.
Boosting (iteration 3)
Code
# Fit a tree to residuals
tree = DecisionTreeRegressor(max_depth=d)
tree.fit(x_obs, residuals);
f_b = tree.predict(x_obs)
f_b_grid = tree.predict(x_grid.reshape(-1, 1))
# Update model
f_hat += lambda_ * f_b
f_hat_grid += lambda_ * f_b_grid
plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_)
# Update residuals
residuals -= lambda_ * f_b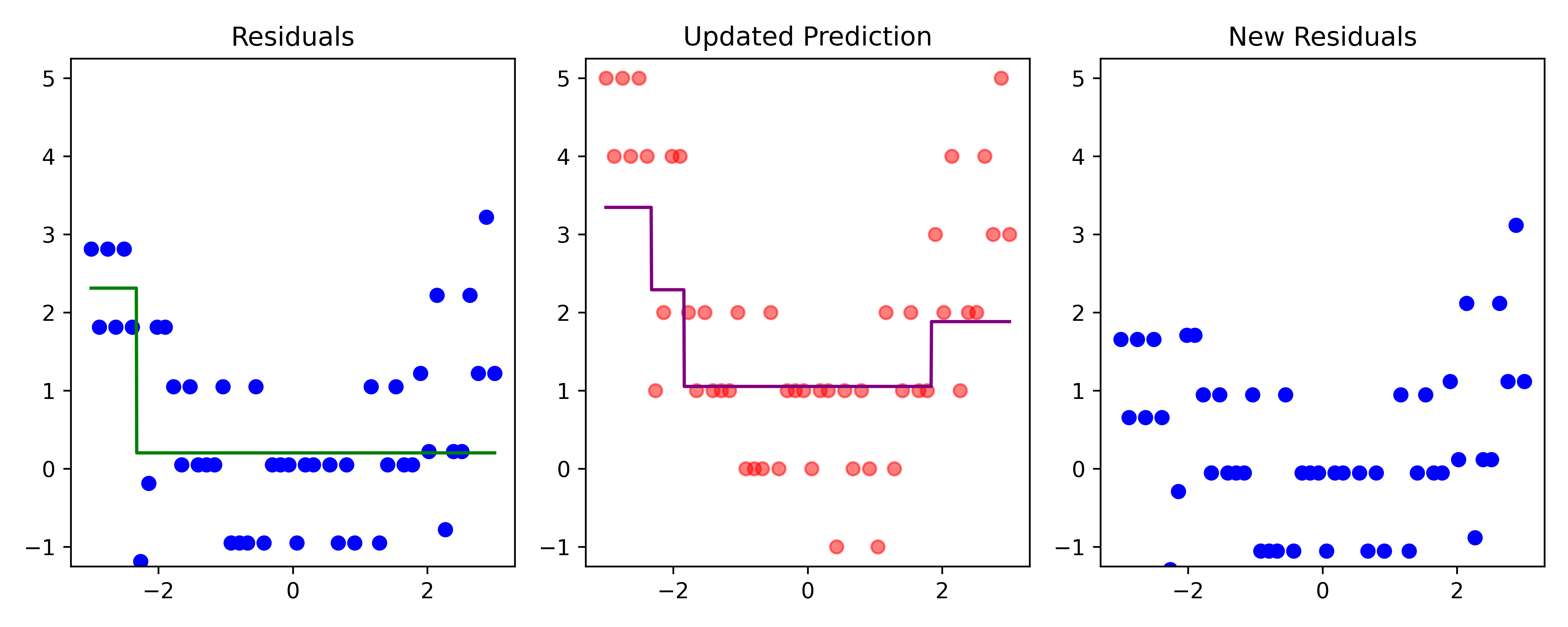
Here, \lambda=\frac12 is the learning rate.
Boosting (iteration 4)
Code
# Fit a tree to residuals
tree = DecisionTreeRegressor(max_depth=d)
tree.fit(x_obs, residuals);
f_b = tree.predict(x_obs)
f_b_grid = tree.predict(x_grid.reshape(-1, 1))
# Update model
f_hat += lambda_ * f_b
f_hat_grid += lambda_ * f_b_grid
plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_)
# Update residuals
residuals -= lambda_ * f_b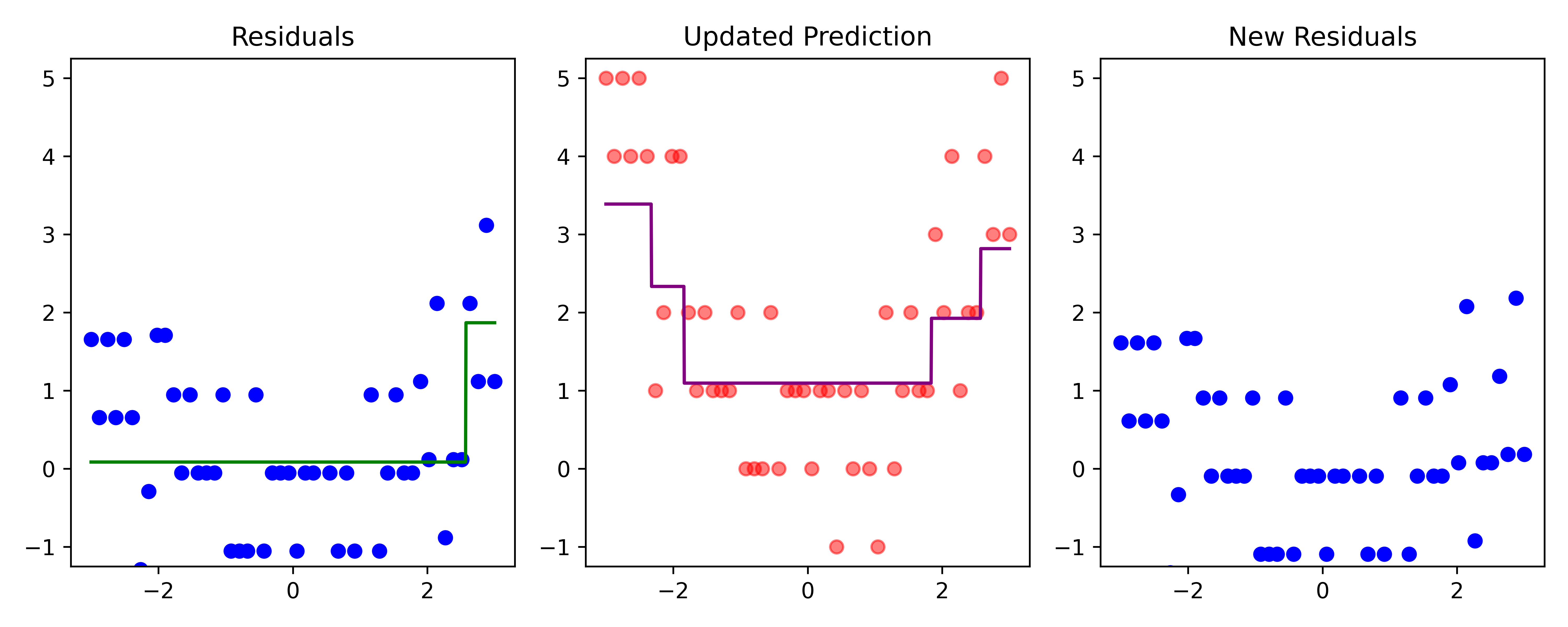
Here, \lambda=\frac12 is the learning rate.
Boosting (iteration 5)
Code
# Fit a tree to residuals
tree = DecisionTreeRegressor(max_depth=d)
tree.fit(x_obs, residuals);
f_b = tree.predict(x_obs)
f_b_grid = tree.predict(x_grid.reshape(-1, 1))
# Update model
f_hat += lambda_ * f_b
f_hat_grid += lambda_ * f_b_grid
plot_boosting_iteration(df, x_grid, f_hat, residuals, f_hat_grid, d, lambda_)
# Update residuals
residuals -= lambda_ * f_b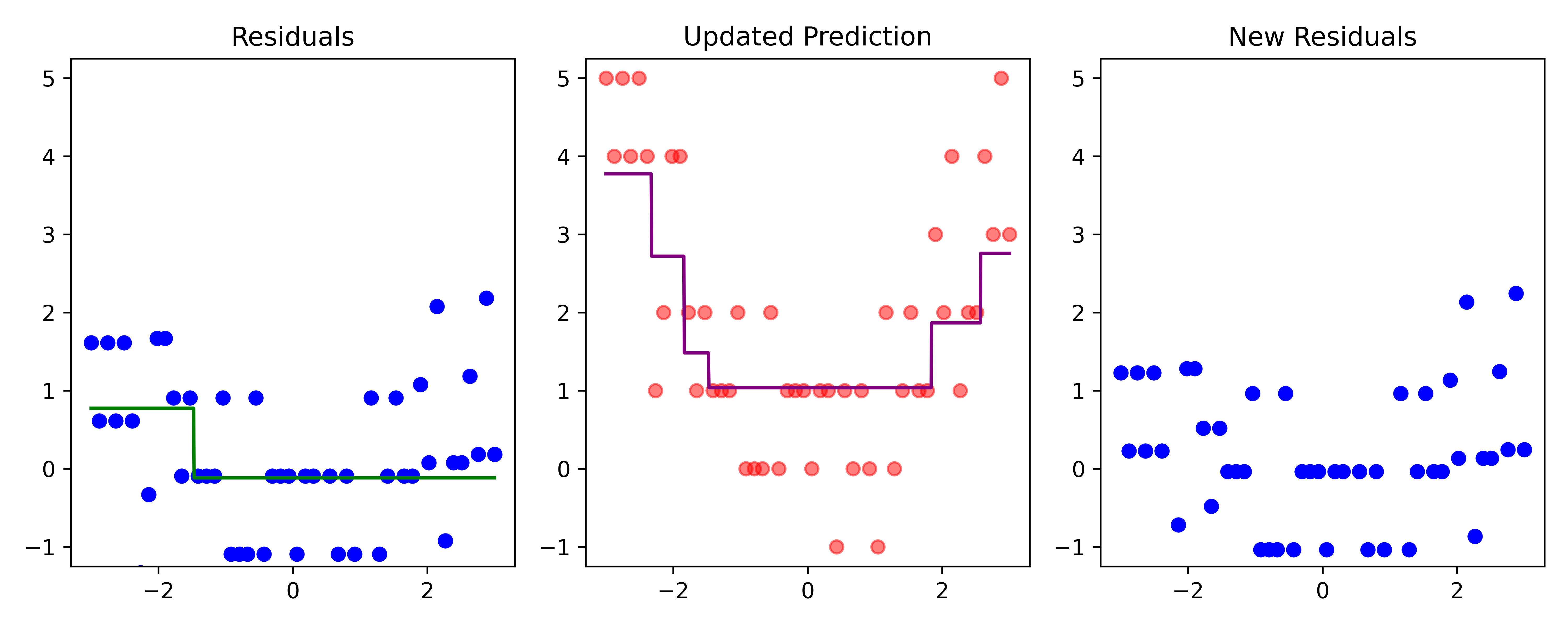
Here, \lambda=\frac12 is the learning rate.
Sensitivity to training data orientation
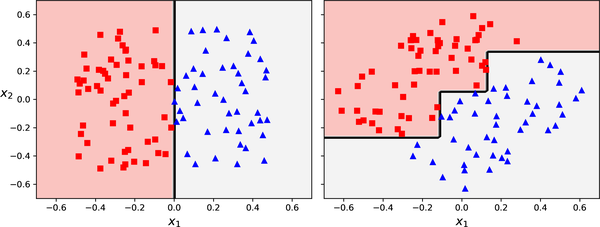
An example of a dataset which is rotated and fit to decision trees.
Source: Aurélien Geron (2022), Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd Edition, Figure 6-7
References