Week 2: Data structures, importation and exportation

Learning outcomes

By the end of this topic, you should be able to

  • run R and RStudio on your own computer
  • understand how to use R and R Studio
  • recognise and create different data structures in R
  • demonstrate the advantages of different data structures
  • extract information from different data structures
  • perform mathematical and set operations
  • import external data of different formats into R
  • export R data into a variety of formats

Work Environment: R and RStudio

Why R and R Studio?

  • In the previous R lecture, we relied on the Ed platform to execute our R codes.
  • This was to ease our way into R programming, but in ‘real life’ you won’t be programming on Ed!
  • In other courses, and potentially in future jobs, you are likely to use R Studio for all your R programming.
  • For the main assignment of this course, you will also need to have installed R and R Studio on your computer.

Installing R and RStudio

  • While “R” is the main software, “RStudio” is an integrated development environment which makes using R more convenient.
  • Download instructions for both can be found here.
  • On the side of the page you can select download instructions for Windows or Mac. If you are using Linux, I trust you can work it out yourself :-).
  • Once you have installed R/RStudio, I strongly recommend watching this video as it walks you through the basics of using RStudio itself (and, as one YouTube user puts it, “this video of yours is better than 4 2-hour lectures from my professor trying to explain how Rstudio works to us”).

Data structures

Data structures - Vectors - page 51

  • The basic data structure in R is the vector (a sequence of data points), which we have encountered before
(myVector <- c(7,11,13)) # Create a vector called 'myVector'
[1]  7 11 13
myVector * 3
[1] 21 33 39
myVector[1] # Get the first element
[1] 7
myVector[3] # Get the third element
[1] 13
  • We now look into some more operations we can perform on vectors.

Vector operations - Some basic functions - Page 87

  • length(): returns the length of a vector.
  • sort(): sorts the elements of a vector, in increasing or decreasing order.
  • rev(): rearranges the elements of a vector in reverse order.
  • rank(): returns the vector of ranks of the elements.
  • head(): returns the first few elements of a vector.
  • tail(): returns the last few elements of a vector.

Vector operations - Examples - Page 87-88

x  <- c(1,3,6,2,7,4,8,1,0,8)
length(x)
[1] 10
sort(x)
 [1] 0 1 1 2 3 4 6 7 8 8
sort(x, decreasing=TRUE)
 [1] 8 8 7 6 4 3 2 1 1 0
rev(x)
 [1] 8 0 1 8 4 7 2 6 3 1
rank(x)
 [1] 2.5 5.0 7.0 4.0 8.0 6.0 9.5 2.5 1.0 9.5
head(x, 3)
[1] 1 3 6
tail(x, 2)
[1] 0 8

Note: The largest value of rank(x) is not always equal to length(x), as there could be a tie of largest values.

Set operations - Page 99

R allows for set operations on vectors

A <- c(4,5,2,7)
B <- c(2,1,7)
intersect(A,B)
[1] 2 7
union(A,B)
[1] 4 5 2 7 1
setdiff(A,B)
[1] 4 5
setdiff(B,A)
[1] 1
is.element(A,B)
[1] FALSE FALSE  TRUE  TRUE
is.element(B,A)
[1]  TRUE FALSE  TRUE

Because is.element is used often, R also provides a special operator %in% as shorthand:

4 %in% A
[1] TRUE
A %in% B
[1] FALSE FALSE  TRUE  TRUE

Set Operations - Exercise

Given that

A <- c(4,5,2,7)
B <- c(2,1,7,3)
C <- c(2,3,7)

Calculate

  • the collection of elements of A and B that only belong to one set
union(setdiff(A,B), setdiff(B,A))
[1] 4 5 1 3
  • the number of elements that belong to A and B and C
length(intersect(intersect(A,B), C))
[1] 2

Extracting elements from vectors - indexing

  • We saw before that to extract the ith element of a vector, we write myVector[i]. This is called indexing.

  • There are more methods for indexing which often prove useful:

vec <- c(2,5,6,8,10)
vec[c(2,3,4)] # Gets the 2nd, 3rd and 4th elements
[1] 5 6 8
vec[2:4] # Does the same but in shorter notation
[1] 5 6 8
vec[-3] # Gets all elements *except* the 3rd
[1]  2  5  8 10
vec[-c(1,5)] # Gets all elements *except* the 1st and 5th
[1] 5 6 8

Extracting elements from vectors - logical masks

There is another extremely useful way of extracting from vectors which is ‘logical masks’. This works by specifying whether each element will be extracted using logical values.

vec
[1]  2  5  6  8 10
vec[c(T, F, T, T, F)] # Any index with T (for TRUE) gets returned
[1] 2 6 8

The above shows that any index with T gets returned. It is a somewhat contrived example because we must specify T/F for each index. Logical masks are more useful in situations as this one:

vec[vec > 5] 
[1]  6  8 10

Indeed, we easily extracted all elements greater than 5 from vec, effectively “filtering” it.

Extracting elements from vectors - three useful functions

x = c(1, 9, 0, 0, -5, 9, -5)
which(x == 0) # returns indices which satisfy the condition
[1] 3 4
which.max(x) # returns the index of the *first* occurrence of the maximum
[1] 2
which.min(x) # returns the index of the *first* occurrence of the minimum value
[1] 5
which(x == min(x)) # same as which.min, but it returns *all* that satisfy the condition
[1] 5 7

Extracting elements from vectors - Exercise

name=c("Adam", "Bob", "Caitlin", "Josephine", "Jinxia")
height=c(165,182,178,160,155)
weight=c(50,85,67,55,48)
income=c(80,90,60,50,210)

What is the average height for people that are more than 60kg?

# We can get the logical mask
weight > 60
[1] FALSE  TRUE  TRUE FALSE FALSE
# And use this on height
height[weight > 60]
[1] 182 178
# And then take the average
mean(height[weight > 60])
[1] 180

What are the names of people with a height < 170

# Using logical masks
name[height < 170]
[1] "Adam"      "Josephine" "Jinxia"   
# Using indexing
name[which(height < 170)]
[1] "Adam"      "Josephine" "Jinxia"

What are the names of people with a weight less than 66 and income above 70?

name[weight < 66 & income > 70]
[1] "Adam"   "Jinxia"

Data structures - Matrices and arrays - page 51

  • Matrices and arrays are generalisations of vectors.
  • A matrix has two dimensions (hence you need two indices to access a data point).
  • An array allows for even more dimensions (hence you need multiple indices).
  • Like vectors, they can only store a single data type. E.g., every entry must be numeric.
    • While this is a tight constraint, having this constraint improves the efficiency over data frames (which we will see later).
    • This trade-off of constraints for efficiency is very common in programming.

Data structures - Matrices and arrays - page 52

(X <- matrix(1:12, nrow=4, ncol=3, byrow=TRUE))
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12
X[2,3] # Extract the item in the 2nd row and 3rd column
[1] 6
(Y <- matrix(1:12, nrow=4, ncol=3, byrow=FALSE))
     [,1] [,2] [,3]
[1,]    1    5    9
[2,]    2    6   10
[3,]    3    7   11
[4,]    4    8   12
Y[3,2] # Extract the item in the 3rd row and 2nd column
[1] 7
(Z <- array(1:60, dim=c(4,5,3)))
, , 1

     [,1] [,2] [,3] [,4] [,5]
[1,]    1    5    9   13   17
[2,]    2    6   10   14   18
[3,]    3    7   11   15   19
[4,]    4    8   12   16   20

, , 2

     [,1] [,2] [,3] [,4] [,5]
[1,]   21   25   29   33   37
[2,]   22   26   30   34   38
[3,]   23   27   31   35   39
[4,]   24   28   32   36   40

, , 3

     [,1] [,2] [,3] [,4] [,5]
[1,]   41   45   49   53   57
[2,]   42   46   50   54   58
[3,]   43   47   51   55   59
[4,]   44   48   52   56   60
Z[2,3,2] # Extract the item in the 2nd row and 3rd column of the 2nd matrix
[1] 30

Data structures - Matrices and arrays - page 53

How do you interpret a three-dimensional array?

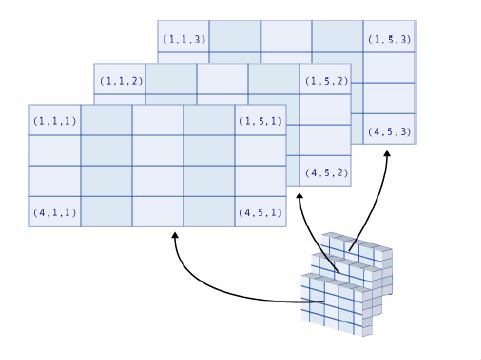
Extracting elements from matrices and arrays

This works under the same rules as it does for vectors, but with multiple dimensions.

(X <- matrix(1:12, nrow=4, ncol=3, byrow=TRUE))
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12
X[c(1,4), 2]  # Extract the items in the 1st and 4th row and 2nd column
[1]  2 11
X[c(1,4), -2] # Extract items in the 1st and 4th row but NOT in the 2nd column
     [,1] [,2]
[1,]    1    3
[2,]   10   12
X[c(1,4), -c(2, 3)] # Extract items in the 1st and 4th row but NOT in the 2nd or 3rd columns
[1]  1 10

We can also omit one of the indices entirely

X[2,]
[1] 4 5 6

As you can see, this extracts the entire second row. Leaving the second dimension empty can be thought of as putting no conditions on it, which means we return everything.

Recycling - Pages 86-87

Given an operation on two vectors/matrices/arrays of different lengths, R will complete the shortest data structure by repeating its elements from the beginning. We call this behaviour ‘recycling’:

x <- c(1,2,3,4,5,6)
y <- c(1,2,3)
x + y
[1] 2 4 6 5 7 9

Another example is below, where the vector 1:3 is repeated to fill in a matrix:

matrix(1:3, ncol=3, nrow=4)
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    2    3    1
[3,]    3    1    2
[4,]    1    2    3

Merging - Merging columns - Page 89

You can merge vectors or matrices together to create a new matrix with functions cbind() and rbind().

(B <- cbind(1:4,5:8))
     [,1] [,2]
[1,]    1    5
[2,]    2    6
[3,]    3    7
[4,]    4    8
(C <- cbind(B, 9:12))
     [,1] [,2] [,3]
[1,]    1    5    9
[2,]    2    6   10
[3,]    3    7   11
[4,]    4    8   12

Can you guess what rbind() does?

Matrix operations - Pages 315-316-317

  • You can perform ‘usual’ mathematical operations on matrices.
  • What are the mathematical meanings of the operations performed below?
(A <- matrix(c(2,3,5,4), nrow=2, ncol=2, byrow=T))
     [,1] [,2]
[1,]    2    3
[2,]    5    4
(B <- matrix(c(1,2,8,7), nrow=2, ncol=2, byrow=F))
     [,1] [,2]
[1,]    1    8
[2,]    2    7
(I2 <- diag(2)) # identity matrix of size 2x2
     [,1] [,2]
[1,]    1    0
[2,]    0    1
A+B 
     [,1] [,2]
[1,]    3   11
[2,]    7   11
A*B
     [,1] [,2]
[1,]    2   24
[2,]   10   28
A/B
     [,1]      [,2]
[1,]  2.0 0.3750000
[2,]  2.5 0.5714286
A%*%I2
     [,1] [,2]
[1,]    2    3
[2,]    5    4
A%*%B
     [,1] [,2]
[1,]    8   37
[2,]   13   68
t(B)
     [,1] [,2]
[1,]    1    2
[2,]    8    7

Note: the diag() function has other use cases (see R Help or type ?diag if you are curious).

Matrix operations - the solve() function - Pages 316-317

  • The solve(A,b) function can be used to solve \(Ax = b\), for \(x\). Here \(b\) can be a vector or a matrix.
  • If solve() is used with only one argument, e.g. solve(A), it will return the inverse of a matrix (if it exists).
(A <- matrix(1:4, ncol=2))
     [,1] [,2]
[1,]    1    3
[2,]    2    4
(x <- solve(A, c(1,1)))
[1] -0.5  0.5
A%*%x 
     [,1]
[1,]    1
[2,]    1
solve(A) %*% A
     [,1] [,2]
[1,]    1    0
[2,]    0    1

Matrix operations - The function apply() - Page 93

The function apply() is often quite handy. It applies a given function to the elements of all rows (MARGIN=1) or all columns (MARGIN=2) of a matrix.

(X <- matrix(c(1:4, 1, 6:8), nrow = 2))
     [,1] [,2] [,3] [,4]
[1,]    1    3    1    7
[2,]    2    4    6    8
apply(X, MARGIN=1, FUN=median)
[1] 2 5
apply(X, MARGIN=2, FUN=mean)
[1] 1.5 3.5 3.5 7.5

Other functions you could use: rowSums(), colSums(), rowMeans(), colMeans().

Matrix operations - Exercise

Given a \(3\times 3\) matrix X

X <- matrix(1:9, nrow = 3)
  • Use function apply to create a vector called row.sums containing the row marginal sums of X (i.e. the sum of elements within each row)
(row.sums <- apply(X, 1, sum))
[1] 12 15 18
  • Do the same to create a vector called col.sums containing the column marginal sums of X
(col.sums <- apply(X, 2, sum))
[1]  6 15 24
  • Verify with a relational operation that sum(row.sums) = sum(col.sums) = sum(X). Make sure you see why that should be the case.
(sum(row.sums) == sum(col.sums)) && (sum(X) == sum(row.sums))
[1] TRUE

Important note on data structures

Do not confuse ‘data structure’ (vector, matrix, array,…) with ‘data type’ (which we saw in Week 1). A ‘data type’ refers to the type of information (numerical, character, logical, etc.) while a ‘data structure’ refers to how we store (or structure!) the information (in a vector, matrix, data frame, etc.)

This is also an internal (and important) distinction within R. If we want to check the type of information, we use typeof:

typeof(2)
[1] "double"
typeof("Hello")
[1] "character"

If we try this on a data structure however, we can see that it actually tells us the type of the objects inside the structure.

typeof(c(1,2,3))
[1] "double"
typeof(matrix("hi", nrow = 3, ncol = 3))
[1] "character"

To determine the structure itself, we use class.

class(matrix("hi", nrow = 3, ncol = 3))
[1] "matrix" "array" 
class(data.frame(GENDER=c("F","M","M","F")))
[1] "data.frame"
class(c(1,2,3))
[1] "numeric"
class(c("ACTL1101", "ACTL2131", "ACTL3142"))
[1] "character"

Data structures - Lists - page 53

Elements stored in vectors, matrices or arrays need to be of the same type (and R automatically converts them to the same type if they are not).

myVector <- c(1,2,"A", TRUE)
myVector
[1] "1"    "2"    "A"    "TRUE"
typeof(myVector)
[1] "character"

Lists can group together, in one structure, data of different types without altering them.

myList <- list(TRUE, my.matrix=matrix(1:4, nrow=2), c(1+2i,3), "R is my friend")
myList
[[1]]
[1] TRUE

$my.matrix
     [,1] [,2]
[1,]    1    3
[2,]    2    4

[[3]]
[1] 1+2i 3+0i

[[4]]
[1] "R is my friend"

The double brackets [[1]] are indicative of a list, and become important to how we extract values in the next slide.

Note that the second item here has a LHS and RHS. When we supply a LHS this “names” the entry in the list, and if we do not, it is left unnamed.

Extracting values from lists

  • The notation to extract from lists is similar to that for vectors, but there is a small twist.
  • To extract a single items form a list, use [[]].
myList[[3]] # this returns the third item of the list (as "itself")
[1] 1+2i 3+0i

To extract several items, use [], but note this will return another list!

myList[1:2] # this returns the 1st and 2nd items of the list, as a list
[[1]]
[1] TRUE

$my.matrix
     [,1] [,2]
[1,]    1    3
[2,]    2    4

We can also use the names of items for extraction.

myList$my.matrix
     [,1] [,2]
[1,]    1    3
[2,]    2    4

Data structures - Lists - Exercise

Consider ‘myList’ given before as

myList <- list(TRUE, my.matrix=matrix(1:4, nrow=2), c(1+2i,3), "R is my friend")
  1. How many elements do we have in the object myList?
length(myList)
[1] 4
  1. Do all elements have the same data types?
sapply(myList, typeof) # similar to apply, but works on other data types too
              my.matrix                         
  "logical"   "integer"   "complex" "character"
  1. If you did not know this was a list, how would you find out?
class(myList)
[1] "list"
  1. Does each element have its own name?

No. Only the second item is named, as my.matrix.

Data structures - Data frames - page 54

A data.frame in R is a table where

  • each row represents a single observation (e.g., an individual)
  • each column represents a single variable, which must be of the same data type across all rows

Data frames are widely used in R

  • flexibility of having multiple data types
  • in many cases, a dataset can be expressed as a data frame

Data structures - Data frames

BMI <- data.frame(
  Gender=c("M","F","M","F"),
  Height=c(1.83,1.78,1.80,1.55),
  Weight=c(77,68,66,48),
  Names=c("Ben","Katja","Anthony","Jinxia"))

BMI
  Gender Height Weight   Names
1      M   1.83     77     Ben
2      F   1.78     68   Katja
3      M   1.80     66 Anthony
4      F   1.55     48  Jinxia
str(BMI)
'data.frame':   4 obs. of  4 variables:
 $ Gender: chr  "M" "F" "M" "F"
 $ Height: num  1.83 1.78 1.8 1.55
 $ Weight: num  77 68 66 48
 $ Names : chr  "Ben" "Katja" "Anthony" "Jinxia"

You can access a specific variable using the $ command

BMI$Gender
[1] "M" "F" "M" "F"

Merging - Merging columns of data frames - Page 89-91

  • You may need to add to a dataset some variables from another dataset (which has the same subjects).
  • To do so, you can use the merge() function.
  • Be careful of what happens when not all subjects are present in both datasets!
X <- data.frame(GENDER=c("F","M","M","F"),
ID=c(123,234,345,456),
NAME=c("Mary","James","James","Olivia"),
Height=c(170,180,185,160))

Y <- data.frame(GENDER=c("M","F","F","M"),
ID=c(345,456,123,234),
NAME=c("James","Olivia","Mary","James"),
Weight=c(80,50,70,60))
X
  GENDER  ID   NAME Height
1      F 123   Mary    170
2      M 234  James    180
3      M 345  James    185
4      F 456 Olivia    160
Y
  GENDER  ID   NAME Weight
1      M 345  James     80
2      F 456 Olivia     50
3      F 123   Mary     70
4      M 234  James     60
cbind(X,Y)  # Not very useful here
  GENDER  ID   NAME Height GENDER  ID   NAME Weight
1      F 123   Mary    170      M 345  James     80
2      M 234  James    180      F 456 Olivia     50
3      M 345  James    185      F 123   Mary     70
4      F 456 Olivia    160      M 234  James     60
merge(X,Y)  # This is what we want
  GENDER  ID   NAME Height Weight
1      F 123   Mary    170     70
2      F 456 Olivia    160     50
3      M 234  James    180     60
4      M 345  James    185     80

Any individual not present in both datasets will be lost.

Z <- data.frame(GENDER=c("M","F","F","F"),
ID=c(345,456,123,999),
NAME=c("James","Olivia","Mary","Jennifer"),
Age=c(21,19,23,99))
Z
  GENDER  ID     NAME Age
1      M 345    James  21
2      F 456   Olivia  19
3      F 123     Mary  23
4      F 999 Jennifer  99
merge(X,Z)
  GENDER  ID   NAME Height Age
1      F 123   Mary    170  23
2      F 456 Olivia    160  19
3      M 345  James    185  21

You can use the all.x or all.y arguments to force the inclusion of all the subjects of a dataset.

merge(X,Z, all.x = T) # all subjects of first dataset are kept
  GENDER  ID   NAME Height Age
1      F 123   Mary    170  23
2      F 456 Olivia    160  19
3      M 234  James    180  NA
4      M 345  James    185  21
merge(X,Z, all.y = T) # all subjects of second dataset are kept
  GENDER  ID     NAME Height Age
1      F 123     Mary    170  23
2      F 456   Olivia    160  19
3      F 999 Jennifer     NA  99
4      M 345    James    185  21

Data structure - Factors

While handling numeric variables is fairly standard in R, we have not examined how to handle categorical variables. For example in the previous data frame,

Z$GENDER # conceptually, this is a categorical variable
[1] "M" "F" "F" "F"
Z$NAME # this is not, but they are both just treated as strings
[1] "James"    "Olivia"   "Mary"     "Jennifer"

To tell R to treat the former as a categorical variable, we use factor():

gender_as_factor = factor(Z$GENDER)
levels(gender_as_factor) # this shows you all unique factors
[1] "F" "M"

While it is difficult to show you how this is helpful just yet, it will become apparent as we do more data manipulation and visualisation.

When necessary, you can also construct ordered categorical variables.

grades = c("P", "HD", "D", "D", "Something Else", "F", "C", "C")
grades_as_factor = factor(grades, levels = c("F", "P", "C", "D", "HD"), ordered = T)
grades_as_factor # note that "Something Else" becomes NA because it isn't specified in levels
[1] P    HD   D    D    <NA> F    C    C   
Levels: F < P < C < D < HD

Data structure - Summary

Data structure Instruction in R Description
vector c() Sequence of elements of the same nature
matrix matrix() Two-dimensional table of elements of the same nature
array array() More general than a matrix; table with several dimensions
list list() Sequence of R structures of any (and possibly different) nature.
data frame data.frame() Two-dimensional table. The columns can be of different natures, but must have the same length.
factor factor() Vector of character strings associated with a modality table
dates as.Date() Vector of dates
time series ts() Values of a variable observed at several time points

Importation and Exportation

Importing data - text files - Page 64

  • R is a great tool to analyse data… but we first need to get our data into R!
  • There are several functions to import data from a text file. Here we will focus on the read.table and read.csv functions (which are widely used to import excel and csv files), but note that other import functions exist, e.g., read.ftable(), scan(), read.delim().

Importing data - read.table() - Pages 64-66

  • To understand the arguments of the read.table() function, it is beneficial to look at an example of raw data.
  • For example, a file mydata.txt might contain the following:
Name,Age,Gender,Income
John,34,M,30
David,36,M,20
Mary,28,F,25
Josephine,32,F,42
  • As you can see, each item is separated by a comma, and each row or entry is separated by a newline (pressing the Enter key).
  • Based on these observations, we can work out the arguments we have to supply to read.table
Argument name Description
file=path/to/file Location of the file to be read, including its name with extension (mydata.txt in our example)
header=FALSE Indicates whether the variable names are given on the first line of the file. In the example this is the first line Name,Age,Gender,Income
sep=“” This is the field separator character. Values on each line of the file are separated by this character. (e.g. “” = whitespace, “,” = comma, “\(\backslash\)t” = tabulation). In the example this is a comma.
dec=“.” Decimal mark for numbers (“.” or “,”)
  • Using the above example, if mydata.txt is in our working directory, we can read the data using the following:
data <- read.table(file="mydata.txt", header=TRUE, sep=",")
  • If you do this, ‘data’ will be a data.frame containing the dataset from your .txt file (“mydata.txt”)
  • Once imported, note you can visualise the beginning or end of your data by using head(data) or tail(data)
head(data)
       Name Age Gender Income
1      John  34      M     30
2     David  36      M     20
3      Mary  28      F     25
4 Josephine  32      F     42

Working Directories

The concept of directories and working directories tends to cause some confusion among students, so here is a brief explanation:

  • A “directory” just means a folder on your computer 'C:\Users\jose\Desktop\ACTL1101\'
  • The “working directory” is the folder on your computer that R is “working” from.
  • Ideally, this should be a directory containing your R script, and any other files you are using for the task at hand.
  • For example, if you were working on the assignment you may want to put all your files (e.g. script, data, etc.) in 'C:\Users\jose\Desktop\ACTL1101\Assignment'
  • If you had this setup, then to tell R to look for your data or other files there, you would run setwd('C:/Users/jose/Desktop/ACTL1101/Assignment') (note the change to forward slashes).
  • Once you have done this, you could simply execute read.table('mydata.txt', header=T, sep=",") because R is already looking in the right place.

As an aside, when you are working from Ed, all requisite files will already be in your working directory (so you do not need to worry about setting the working directory when using Ed).

Importing data - Exercise - Page 66

In the Ed ‘Exercise Space’ for this week we have placed a dataset in the .txt format called danishfire.txt. It contains claim amounts for three different categories of insurance losses, also with the dates at which the losses occurred.

  • Use the function readLines("danishfire.txt", n=5) to visualize the beginning of the data. Note that at this stage you are just looking at the data, you have not imported it.
  • Import the data and store it in a data frame called danish_fire.
  • Display the first few records of danish_fire by using the head() function.
  • Apply functions class() and str() to danish_fire. What information does this provide you?
  • Calculate the mean of the building losses, as well as the correlation between the building losses and contents losses. Hint: Use functions mean() and cor().

I also encourage you to do this locally (on your own computer)!

Importing data - Solution - Page 66

# Vizualise data using readLines
readLines("danishfire.txt", n=5)
[1] "  Positions     building     contents      profits      total "
[2] " 01/03/1980   1.09809663 5.856515e-01  0.000000000   1.683748" 
[3] " 01/04/1980   1.75695461 3.367496e-01  0.000000000   2.093704" 
[4] " 01/05/1980   1.73258126 0.000000e+00  0.000000000   1.732581" 
[5] " 01/07/1980   0.00000000 1.305376e+00  0.474377745   1.779754" 
# import data, note that the header argument is TRUE
danish_fire <- read.table(file="danishfire.txt", header=TRUE, sep="")
head(danish_fire)
   Positions building  contents   profits    total
1 01/03/1980 1.098097 0.5856515 0.0000000 1.683748
2 01/04/1980 1.756955 0.3367496 0.0000000 2.093704
3 01/05/1980 1.732581 0.0000000 0.0000000 1.732581
4 01/07/1980 0.000000 1.3053760 0.4743777 1.779754
5 01/07/1980 1.244510 3.3674960 0.0000000 4.612006
6 01/10/1980 4.452040 4.2732340 0.0000000 8.725274
class(danish_fire)
[1] "data.frame"
str(danish_fire)
'data.frame':   2167 obs. of  5 variables:
 $ Positions: chr  "01/03/1980" "01/04/1980" "01/05/1980" "01/07/1980" ...
 $ building : num  1.1 1.76 1.73 0 1.24 ...
 $ contents : num  0.586 0.337 0 1.305 3.367 ...
 $ profits  : num  0 0 0 0.474 0 ...
 $ total    : num  1.68 2.09 1.73 1.78 4.61 ...
# some numerical analysis
mean(danish_fire$building)
[1] 1.824408
cor(danish_fire$building, danish_fire$contents)
[1] 0.3271123

Note that function readLines() is useful as it allows you to visualize the beginning of the data file before you import the data, so you know the structure of the data and can determine the arguments of the function read.table().

Importing data - Standard formats (e.g. csv) - Page 67

  • When data is stored under a “standard format” (e.g., csv), most arguments of the function read.table() are fixed.
  • Some R functions are designed to be equivalent to read.table() with several arguments filled with pre-determined values, e.g.,
    • read.csv(): .csv format (csv stands for comma separated values)
movies.data <- read.csv("Movies.csv")
head(movies.data)
  Movie.ID                               Movie.Title Release.Year Runtime
1        1  Harry Potter and the Philosopher's Stone         2001     152
2        2   Harry Potter and the Chamber of Secrets         2002     161
3        3  Harry Potter and the Prisoner of Azkaban         2004     142
4        4       Harry Potter and the Goblet of Fire         2005     157
5        5 Harry Potter and the Order of the Phoenix         2007     138
6        6    Harry Potter and the Half-Blood Prince         2009     153
         Budget      Box.Office
1 $125,000,000  $1,002,000,000 
2 $100,000,000    $880,300,000 
3 $130,000,000    $796,700,000 
4 $150,000,000    $896,400,000 
5 $150,000,000    $942,000,000 
6 $250,000,000    $943,200,000
  • Most datasets you will come across are CSVs, so more often than not read.csv() will do the trick.
  • Still, being comfortable with the more general read.table() is important.

Exporting data - Pages 72-73

Create a data frame that contains only the first 50 rows of danish_fire, and then export this new data set to a folder on your computer.

# Create the new data set
danish.50.only <- danish_fire[1:50,]
# Exporting data to a text file
write.table(danish.50.only, file = "myfile.txt", sep = "\t")
# Exporting data to a csv file
write.csv(danish.50.only, file = "myfile.csv")

Note that the commands above save your data into the working directory.

If you are using R on your computer (not in Ed!), you can specify a different path if you wish, by using file = "path/to/data/myfile.txt".

Homework

Homework Exercise 1

Generate a random vector of 1000 standard normal observations. Then,

  1. Find both the value and the index of the largest observation.
  2. Output all observations within this vector that are larger than 2.
  3. Find the mean of all observations larger than 2.
  4. Compute the total proportion of observations larger than 2.

Homework Exercise 2

Give the R instruction which gives the following output:

> A
    [,1] [,2] [,3]
[1,]   1    5    9
[2,]   2    6   10
[3,]   3    7   11
[4,]   4    8   12

Assuming that A was created as above, predict the outputs of the following instructions:

  • A[3,]
  • A[2,2:3]

Homework Exercise 3

Given two matrices \(A\) and \(B\), where: \[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \quad \text{ and } \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \] Find the following:

  • \(C = A \times B\)
  • \(D = B^{\top}\)
  • \(E = A^{-1}\)
  • \(F\), an identity matrix of size \(5 \times 5\)

Homework Exercise 4

Give the instruction to merge these two tables:

> X
  Gender Weight Names
1      M     80  Jack
2      F     60 Julia
> Y
   Eyes Height Names
1  Blue    180  Jack
2 Green    160 Julia

Homework Exercise 5

Name the main data structures available in R.

Homework Exercise 6

What is the main advantage of the “list” data structure?

Homework Exercise 7

What is the purpose of the following R functions:

  • read.table()
  • read.csv()
  • write.table()
  • write.csv()

Homework Exercise 8

Import the file called Movie.csv into your working directory (and store it as a data frame, with a name of your choice). Note you can find this file under Ed Resources. Then, find the average Runtime of all Harry Potter movies. What happens if you try to find their average Box.Office?

Additional Notes: Extraction from matrices using logical masks - Pages 102-103

By using ‘logical masks’: X[mask]

  • a mask is a matrix of logical values (TRUE or FALSE) of the same size as X, indicating which elements to extract
Mat <- matrix(1:12,nrow=4,byrow=TRUE)
MatLogical <- matrix(c(TRUE,FALSE),nrow=4,ncol=3)
Mat
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12
MatLogical
      [,1]  [,2]  [,3]
[1,]  TRUE  TRUE  TRUE
[2,] FALSE FALSE FALSE
[3,]  TRUE  TRUE  TRUE
[4,] FALSE FALSE FALSE
Mat[MatLogical]
[1] 1 7 2 8 3 9

Additional Notes: The which() function for matrices - Page 104

m <- matrix(c(1,2,3,1,2,3,2,1,3),3,3)
m
     [,1] [,2] [,3]
[1,]    1    1    2
[2,]    2    2    1
[3,]    3    3    3
which(m == 1) 
[1] 1 4 8

The outputs of 1, 4, and 8 can be found by counting from top to bottom and then left to right across the 2 dimensions of the matrix.

However, we can get a more meaningful output

which(m == 1,arr.ind=TRUE)
     row col
[1,]   1   1
[2,]   1   2
[3,]   2   3
# this gives the indices (row and column) of all elements = 1