Week 5: Data visualisation

Learning outcomes

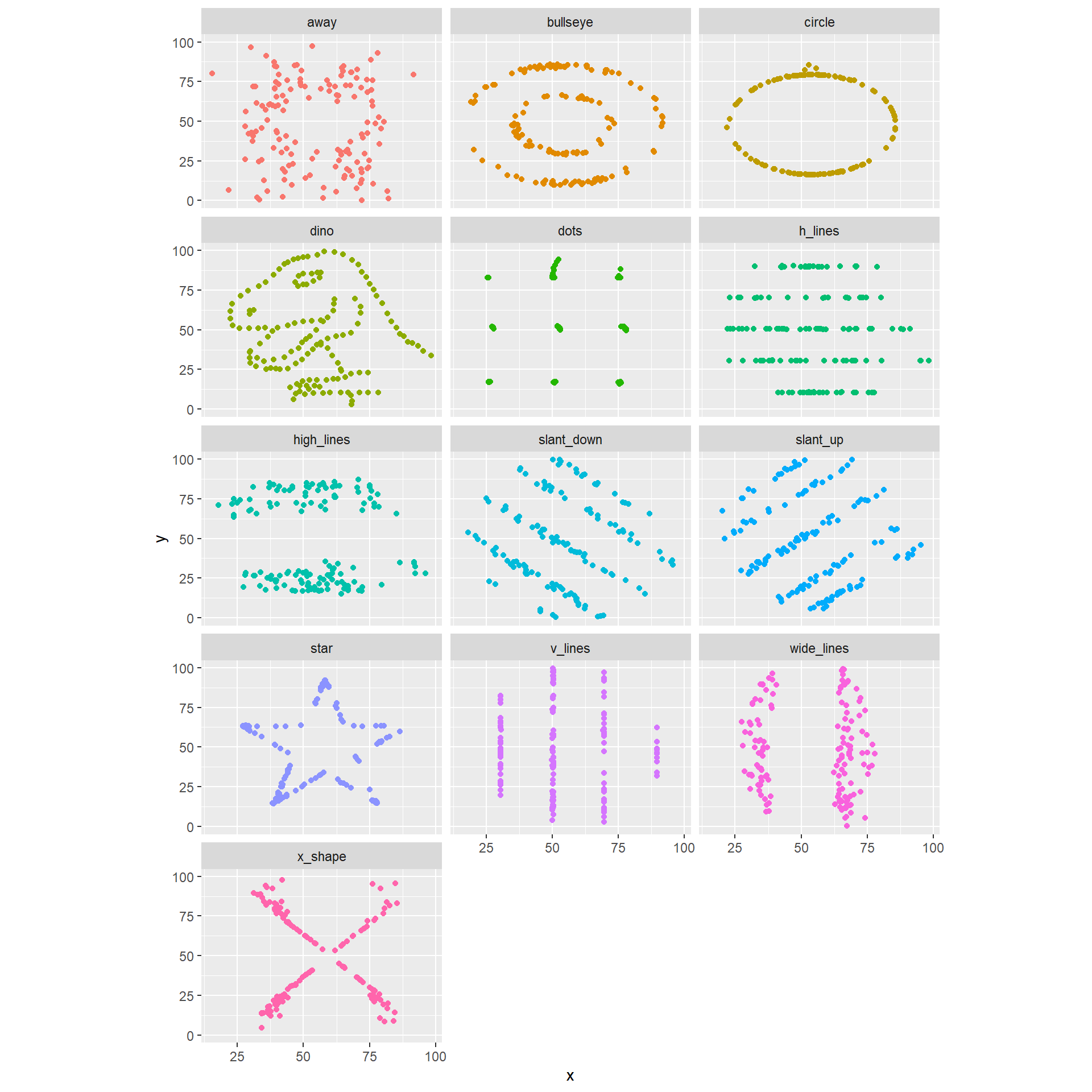
By the end of this topic, you should be able to

  • demonstrate the importance of effective data visualisation
  • choose appropriate visualisation tools for statistical analysis
  • create and edit various plots and curves in R
  • present and summarise data using various visualisations in R

Why do we need visualisation?

Numbers have limitations

  • Statistics are usually not enough, and can sometimes be misleading.
  • Consider for instance the scatterplot below, where we have a sample of two variables \(X,Y\).
  • We see that many different configurations of points produce the same statistical summaries (mean, standard deviation and correlation).

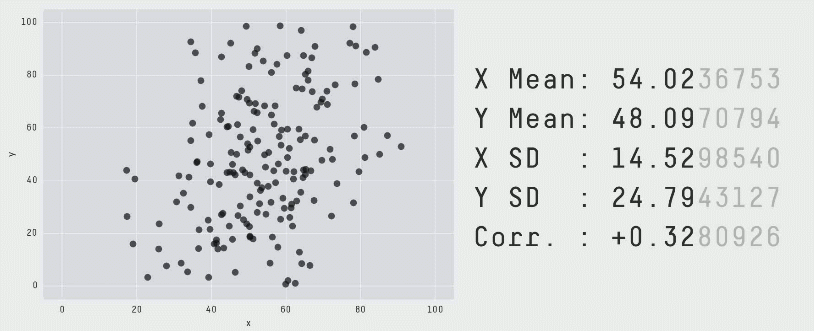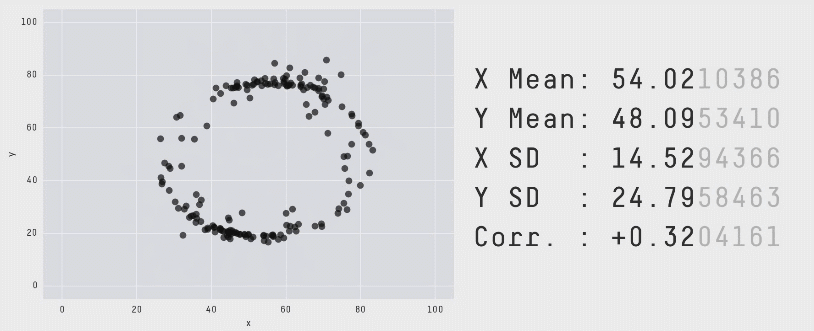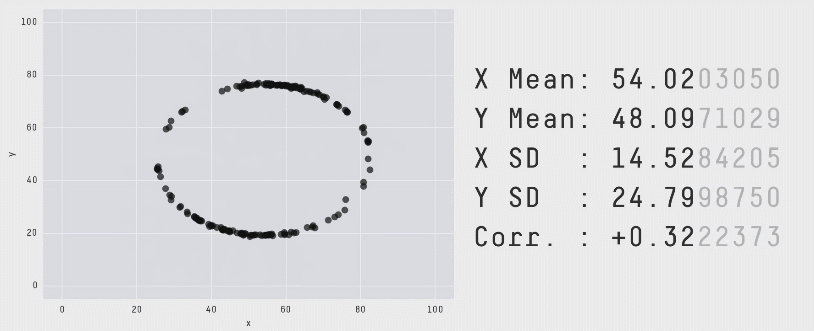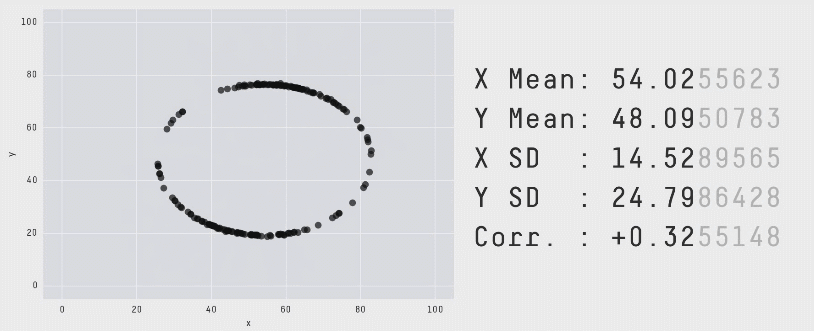
  • The data of the above illustration is included in the R package datasauRus.

  • A similar example is given by the 13 plots below. Again, the numerical summaries of those data sets are essentially the same… but look how different they are. You can even get a dinosaur!

  ggplot(datasaurus_dozen, aes(x=x, y=y, colour=dataset))+
    geom_point()+
    coord_fixed(ratio=0.6)+
    theme(legend.position = "none")+
    facet_wrap(~dataset, ncol=3)

Reference

Why we need visualisation: to be good story tellers

  • Humans spend a lot of time communicating.

  • If you activate different parts in the brains of your audience members, your message will be more memorable and impactful.

  • Data means nothing without context: you should provide a ‘story’ around it.

  • You can include statistics into stories, but statistics alone are rarely enough.

  • A good picture is worth a thousand words!

Goals of visualisation

  • Exploratory visualisations help you understand your data

    • Goals: understand, analyse, confirm
    • Mostly at a high level of granularity (usually we don’t want to “oversimplify” or strip out too much information)

  • Explanatory visualisations help you explain your findings to others

    • Goals: inform, persuade
    • Simplifications can be appropriate, depending on the story you are telling and the target audience

Reference

Effective visualisation: What makes a good story?

  • Knowing exactly what you really want to say: what is the key message you want to convey?

  • Understand your audience

    • What do they want to hear (e.g., formulas? a description of the data? key outcomes?)

    • What is the background of the audience (e.g., a junior actuary? a senior director? your grandmother?)

  • Building up a story

    • There can be different ways of building up stories, but it is usually good to build your arguments ‘bottom-up’: start with general motivation & context and then move towards more specific findings/conclusions.

What makes a good story: Example

  • Let’s say you are an international student at UNSW, and you want to explain to your friends back home that: Australia is a very popular destination for immigrants.

  • Already you have done two key steps:

    • Identify your audience: your friends may not be as mathematically literate as you are, so you should avoid technicalities.
    • Identify what you want to say: here you are trying to make one key point, you are not analysing or exploring. You will need explanatory tools.

  • Then, you need to identify what kind of data and visualisation tools you can use to make your point.

  • As a start, you could point out that Australia has a very positive net immigration (inflows minus outflows), at ~850,000 people for 2019-2022.

  • This is a good start, but a single number is a little boring (and does not provide the full story).

What makes a good story: Example continued

  • A chart like the below, showing monthly inflows and outflows (in different colours), paints a fuller picture and is easy to understand. We also see the drastic drop in immigration that happened during COVID (which could be useful information, depending on the audience).

Source: nytimes.com

What makes a good story: Example continued

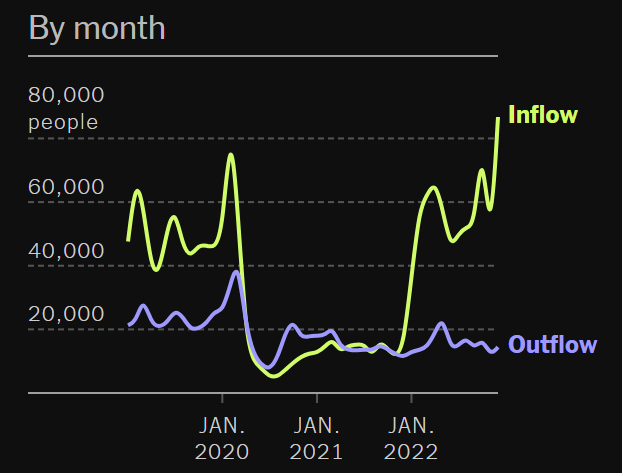
  • The New York Times provides cooler visualisations of migration flows: check their interactive maps here.

  • On the map, yellow circles represent inflows (from different countries), while purple circles represent outflows.

  • In the case of Australia, we see it has a positive net migration with almost all countries on Earth!

  • Your audience should be convinced that Australia is a very popular destination for immigrants.

Effective visualisation: Some considerations

  • Understand what you are trying to present. Is it variables themselves, relationships, trends over time, etc. ?

  • Then, think of the most appropriate tool to present your data

    • scatter plot, line graph, bar graph, histogram, box-plot, etc.

  • Fine tune the presentation to make your figure easy to read and ‘neat’

    • name the axis, use colours, adjust size of points and lines, add a legend, etc.

  • What scale should you use to make your figure the clearest?

Note: for explanatory visualisation, you should highlight/emphasise the key features and avoid unnecessary details.

Reference

Visualisation in “base R”

The plot() and points() functions - Pages 156-158

  • We often want to illustrate the link between two numerical variables.
  • For this, functions plot() and points() are handy.
  • As an example, we consider the data set longley (included in R). Similarly to functions, one can find out more about an inbuilt dataset using help(longley).
  • We are interested to check how number of armed forces and number of unemployed move over time. The following graph would be useful:
plot(longley$Year, longley$Armed.Forces, type="l", lwd = 3, main="Armed Forces and Unemployment (1947-1962)", sub="Exploratory analysis",
     xlab="Year", ylab="Number", ylim=c(0,600))
points(longley$Year, longley$Unemployed, type="l", lwd = 3, col="red")
legend('bottomright', legend=c("Armed Forces","Unemployed"), col=c("black","red"), lty=c(1,1))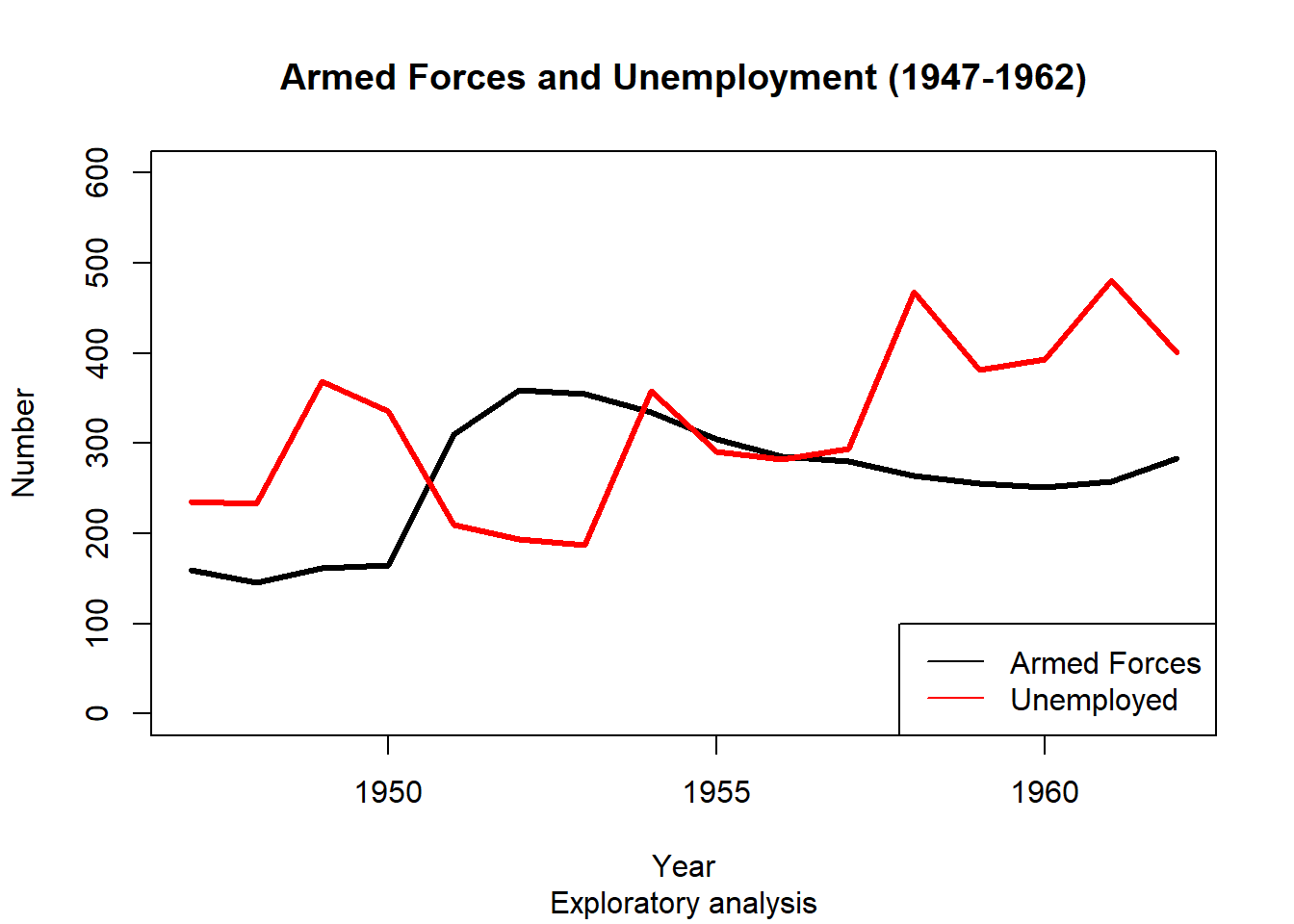

How do we create such a graph?

The plot() function

  • In R, plots are created layer by layer, so we begin with a simple plot and add elements.
  • To create a simple scatterplot we use the plot() function.
  • A scatter plot consists of dots, each of which has a value on the \(x\)-axis and \(y\)-axis.
  • So we give function plot() two arguments: a vector of x values and a vector of y values.
plot(longley$Year, longley$Armed.Forces)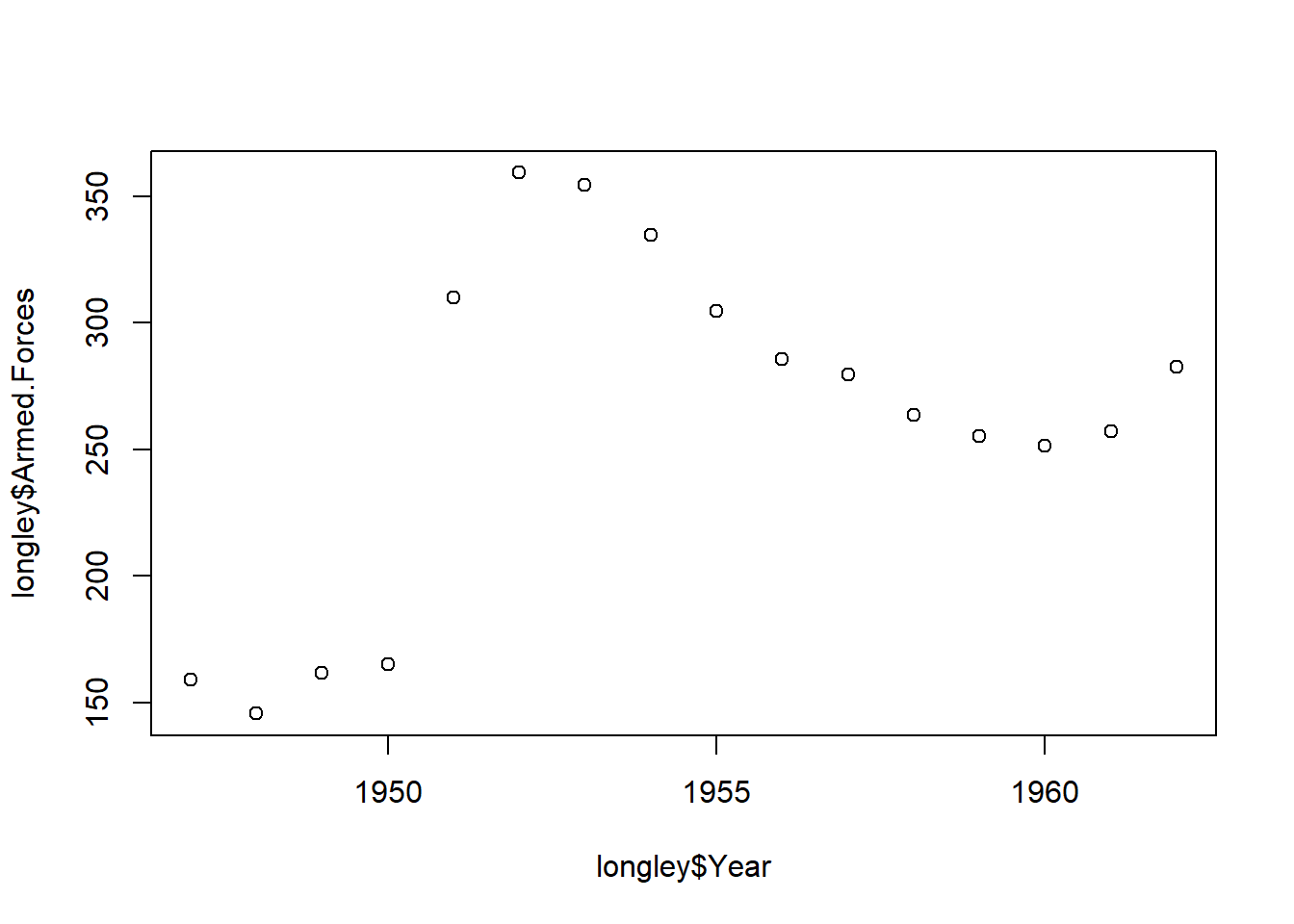

  • A decent start, but could be greatly improved. What would you change about this graph?

Plot() Arguments - type

  • For data observed “through time” (time series) it is appropriate to use a line graph (as opposed to a scatterplot). We can change the plot from points to a line by changing the argument type to l. By default, this was set to p, for ‘point’. Another option is b for ‘both’ line and point.
plot(longley$Year, longley$Armed.Forces, type="l")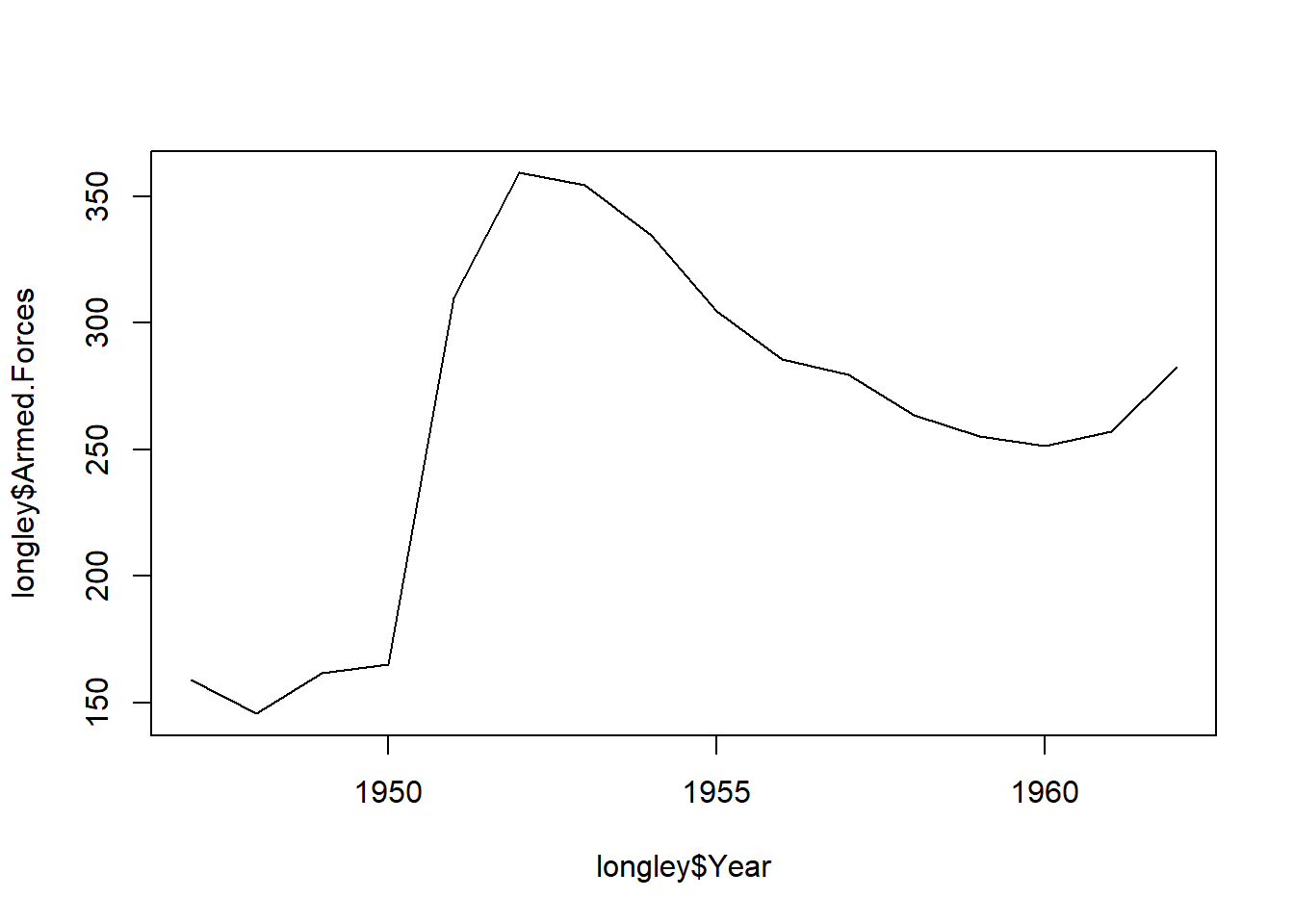

  • Looking better already!

Plot() Arguments - Titles

  • Let us add some titles to improve the readability of our plot
  • We would like to add axis labels, a main title and a subtitle
plot(longley$Year, longley$Armed.Forces, type="l", 
     main="Armed Forces (1947-1962)", sub="Exploratory analysis",
     xlab="Year", ylab="Number")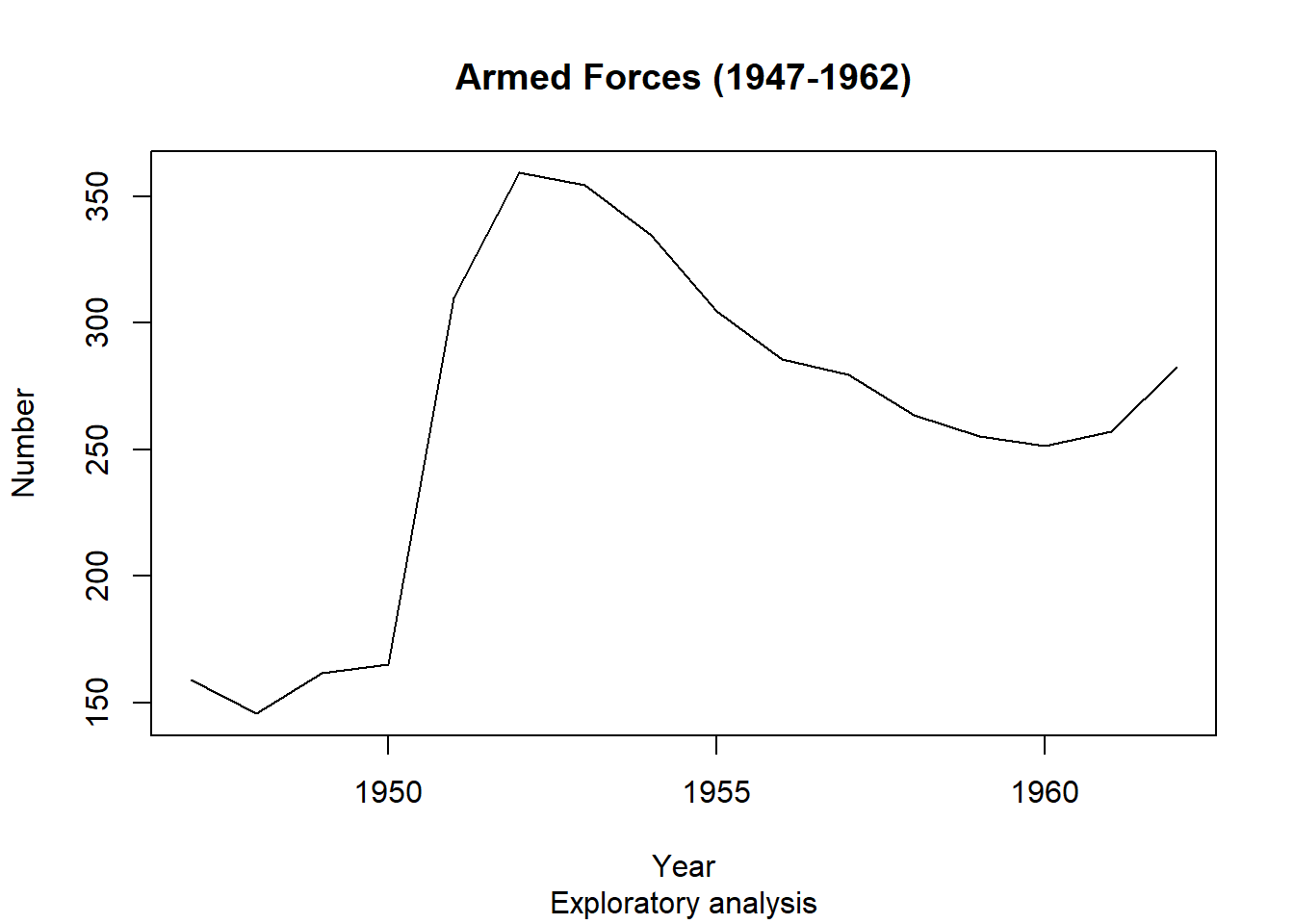

Awesome. Now let us add the second variable, Number Unemployed.

The points() function

  • The points() function has the same basic arguments as plot(), but does not create an entirely new plot.
  • Instead, it adds the points to the previously created plot.
plot(longley$Year, longley$Armed.Forces, type="l", 
     main="Armed Forces and Unemployment (1947-1962)",
     sub="Exploratory analysis",
     xlab="Year", ylab="Number")
points(longley$Year, longley$Unemployed, type="l")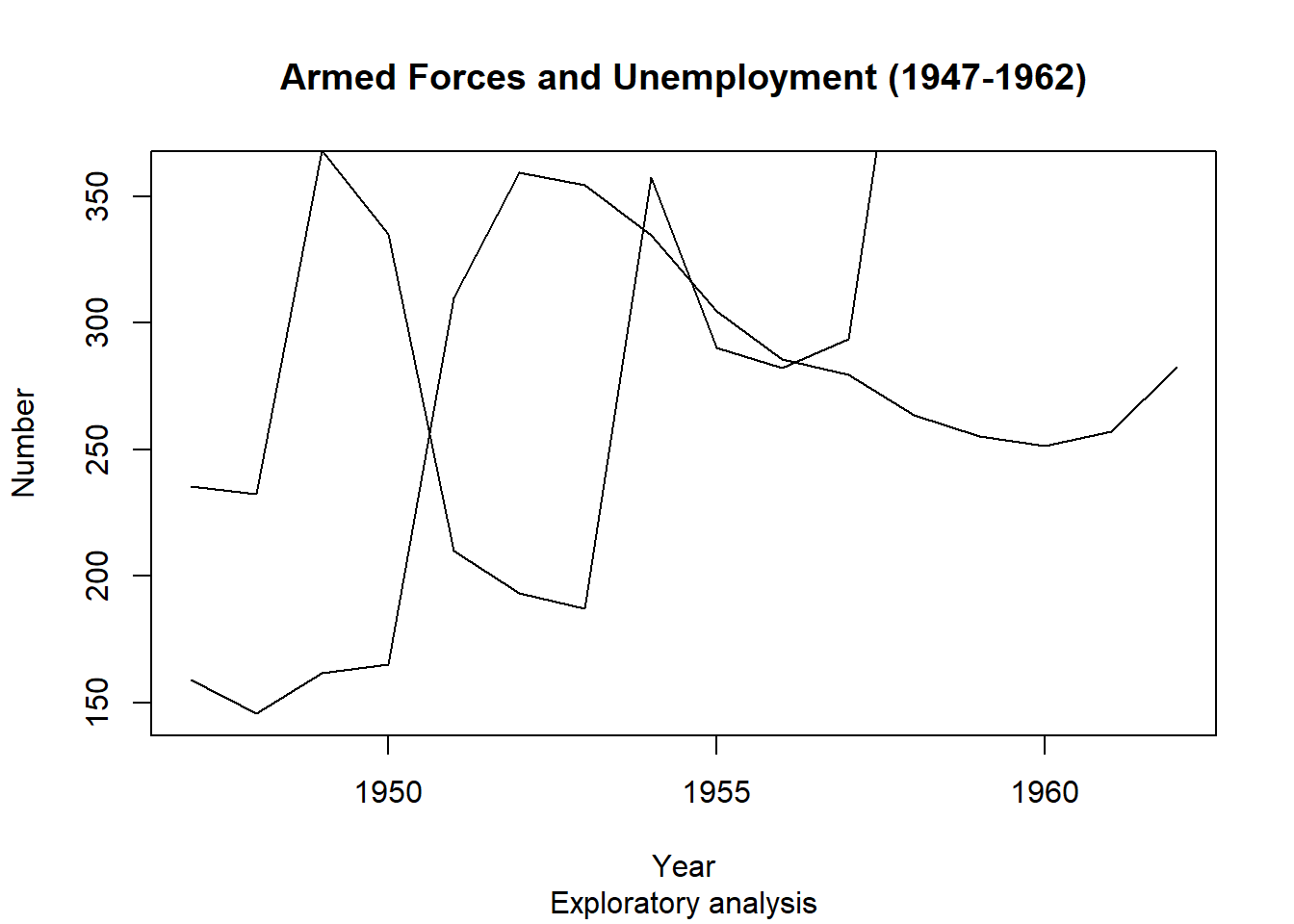

  • Oops! The points() function does not adjust limits of the axis automatically to fit all the new data, so the new line goes off the edge of the plot.

Plot() Arguments - ylim

  • We can change the value of the ylim= argument in plot(), to change the y limits. The input is a vector of length \(2\): c(min, max).
  • The same applies for xlim=.
plot(longley$Year, longley$Armed.Forces, type="l", 
     main="Armed Forces and Unemployment (1947-1962)", sub="Exploratory analysis",
     xlab="Year", ylab="Number", ylim=c(0,600))
points(longley$Year, longley$Unemployed, type="l")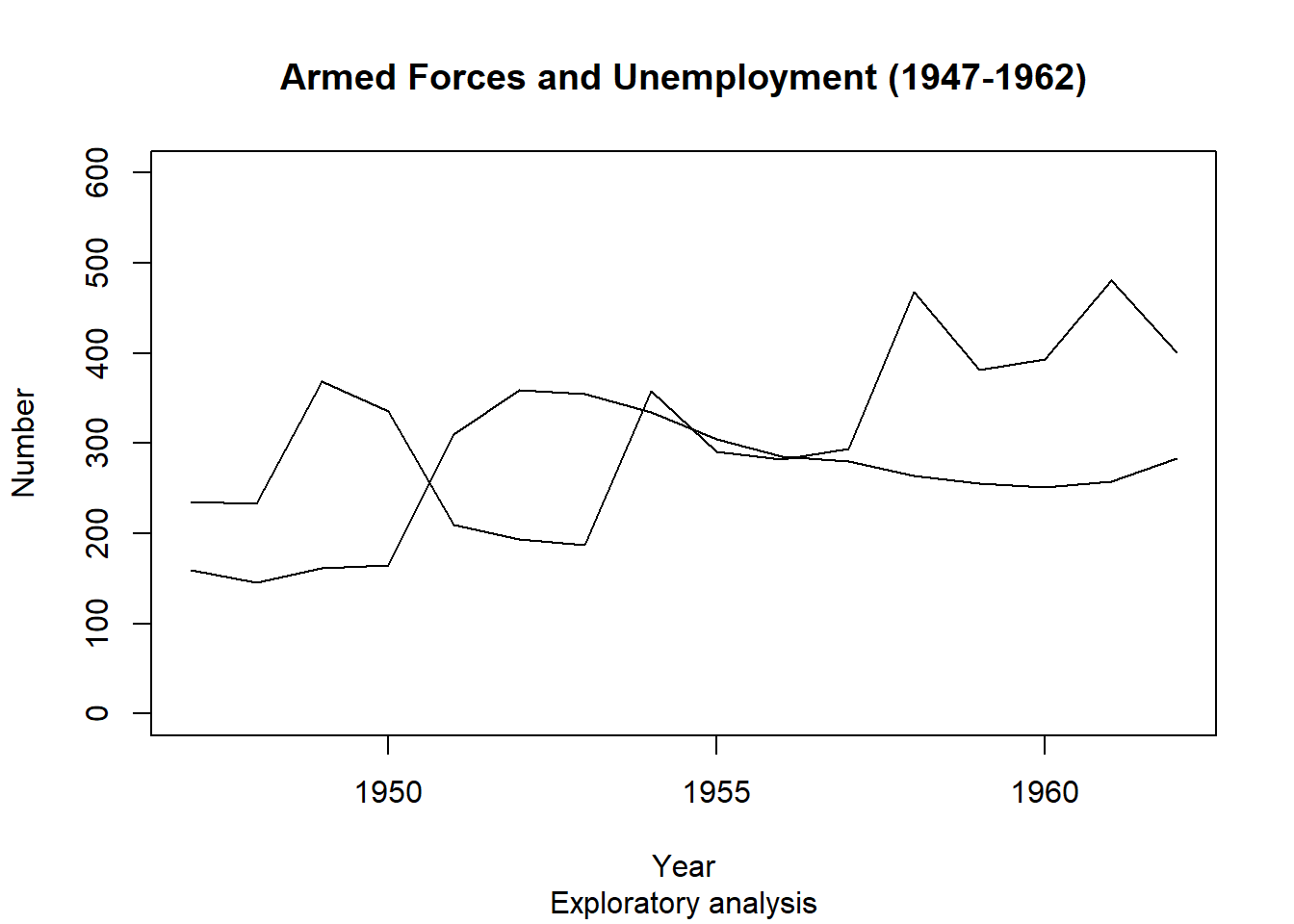

  • Better… but it’s still difficult to distinguish between the lines. Let’s add some colour!

Plot() arguments - col

  • Use the col= argument to choose a colour. Note the syntax: you need to specify the colour by a string, e.g. col = 'red'.
  • We also make the lines broader by using argument lwd = 3, for ‘line width’.
plot(longley$Year, longley$Armed.Forces, type="l", lwd = 3, 
     main="Armed Forces and Unemployment (1947-1962)", sub="Exploratory analysis",
     xlab="Year", ylab="Number", ylim=c(0,600))
points(longley$Year, longley$Unemployed, type="l", lwd = 3, col="red")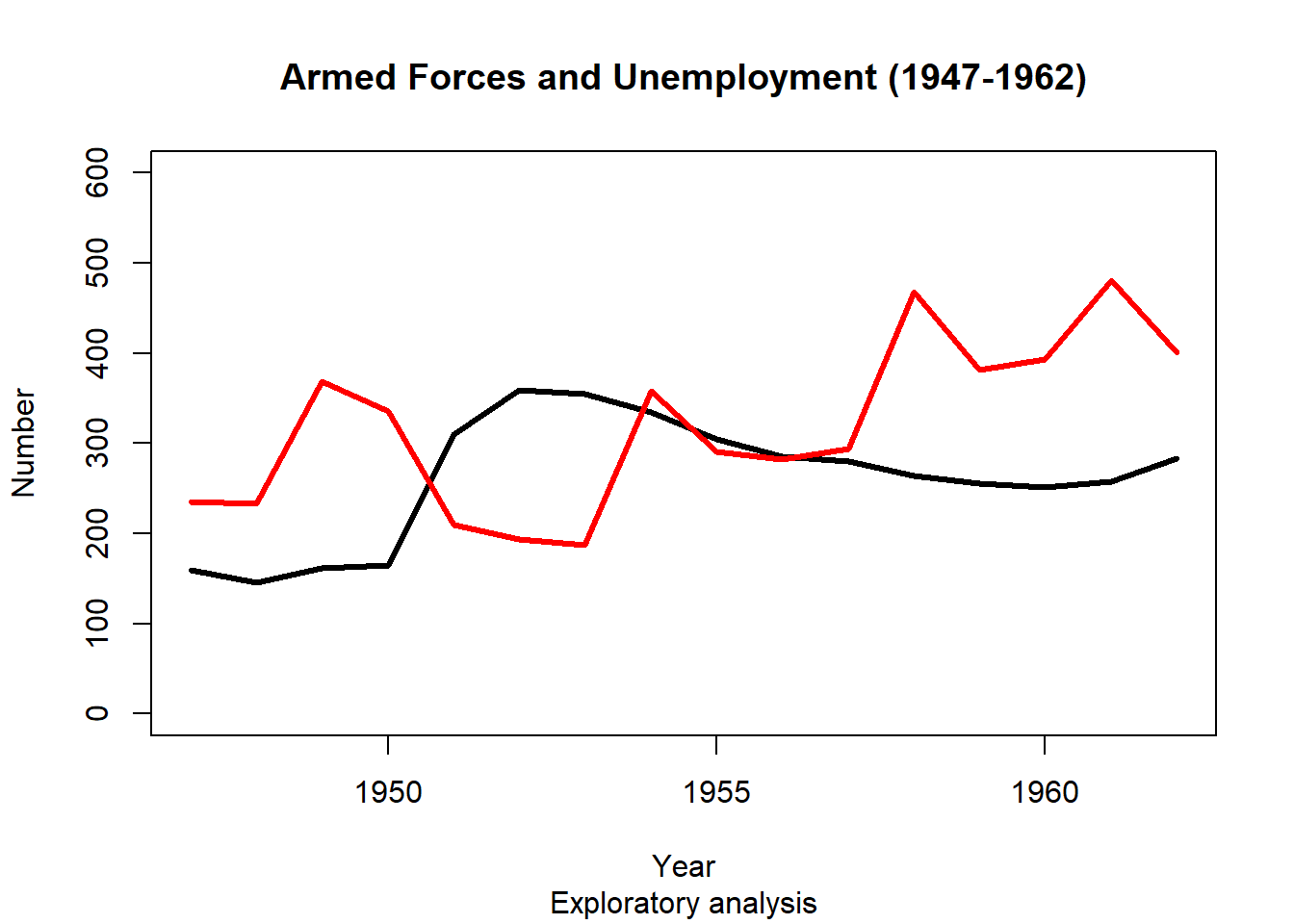

  • For reference, the colors() function returns the names of the 657 colors known to R. You can also Google ‘R colors’ and quickly find the full palette!
head(colors(), 20)
 [1] "white"         "aliceblue"     "antiquewhite"  "antiquewhite1"
 [5] "antiquewhite2" "antiquewhite3" "antiquewhite4" "aquamarine"   
 [9] "aquamarine1"   "aquamarine2"   "aquamarine3"   "aquamarine4"  
[13] "azure"         "azure1"        "azure2"        "azure3"       
[17] "azure4"        "beige"         "bisque"        "bisque1"

legend() function

  • The last missing piece is a legend to help explain which line is which.
  • The legend() function does this for us.
plot(longley$Year, longley$Armed.Forces, type="l", lwd = 3, 
     main="Armed Forces and Unemployment (1947-1962)", sub="Exploratory analysis",
     xlab="Year", ylab="Number", ylim=c(0,600))
points(longley$Year, longley$Unemployed, type="l", lwd = 3, col="red")
legend('bottomright', legend=c("Armed Forces","Unemployed"), col=c("black","red"), lty=c(1,1))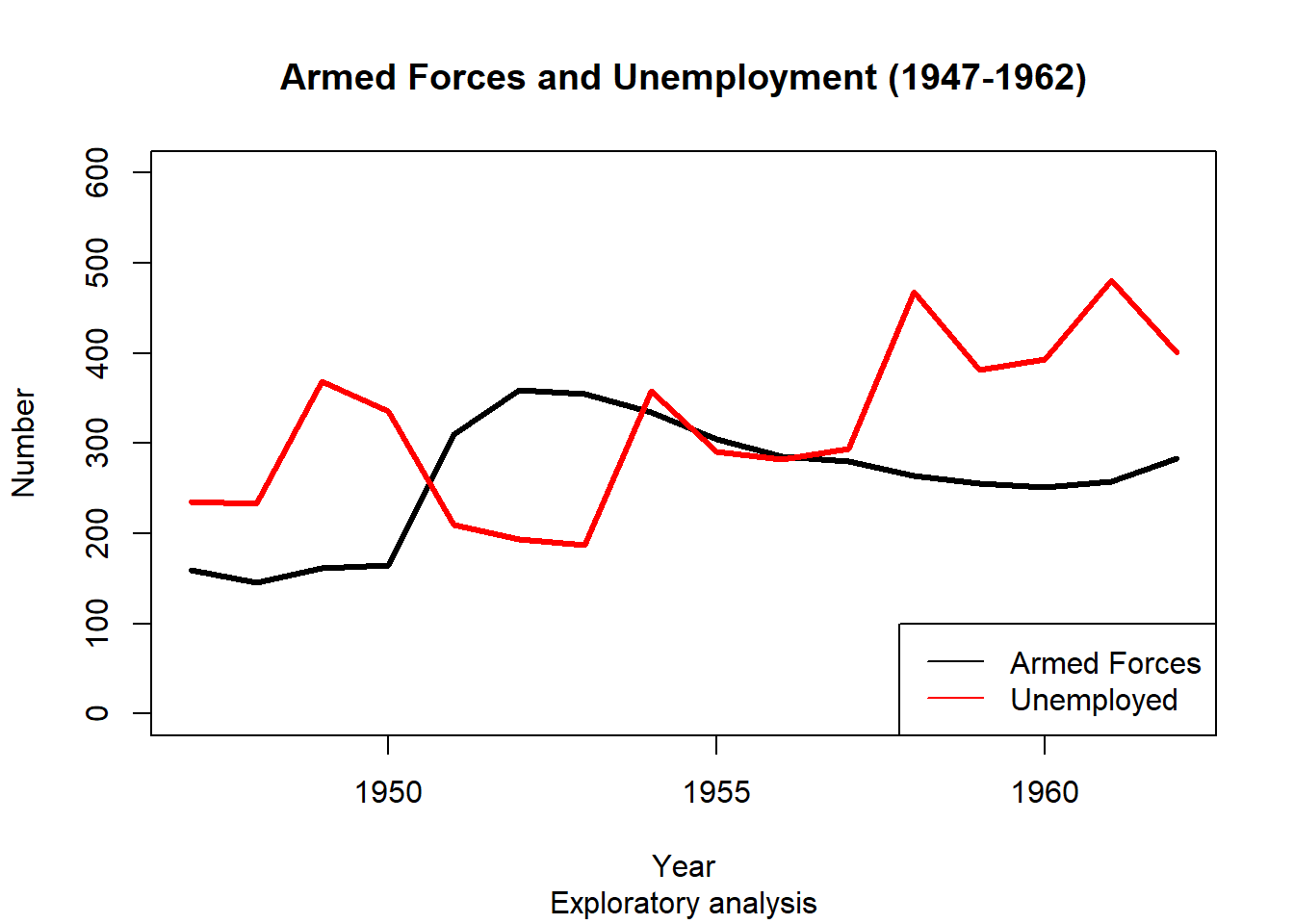

Any trends here?

Remember, if you ever forget how to use these functions, or how one of the arguments works, or just want to learn more about one of these function, using help() is your friend.

Statistical visualisation: other types of plots

  • R has a wide range of built-in functions that can be used to visualise data. Listing them all would be difficult.
  • In the next few slides we mention some more,
  • We will use the dataset school_data2019.csv for illustration purposes.
  • Make sure you import the data and attach it if you want to reproduce the plots.
school_data<-read.csv("school_data2019.csv",header=TRUE)
attach(school_data)
The following objects are masked from school_data (pos = 3):

    Bottom.SEA.Quarter...., Boys.Enrolments, Campus.Type,
    Full.Time.Equivalent.Enrolments,
    Full.Time.Equivalent.Non.Teaching.Staff,
    Full.Time.Equivalent.Teaching.Staff, Geolocation, Girls.Enrolments,
    Governing.Body, ICSEA, ICSEA.Percentile, Indigenous.Enrolments....,
    Language.Background.Other.Than.English....,
    Lower.Middle.SEA.Quarter...., Net.Tax, Non.Teaching.Staff,
    Postcode, Rolled.Reporting.Description, Salary.or.Wages,
    School.Name, School.Sector, School.Type, State, Suburb,
    Taxable.Income, Teaching.Staff, Top.SEA.Quarter....,
    Total.Enrolments, Upper.Middle.SEA.Quarter....

Histogram

  • For a numerical variable, an histogram illustrates the relative frequencies of observations falling inside different intervals.
  • Use argument proba=T to have it on a probability scale.
  • Play with argument break for larger or smaller intervals.
hist(ICSEA, xlab = "ICSEA")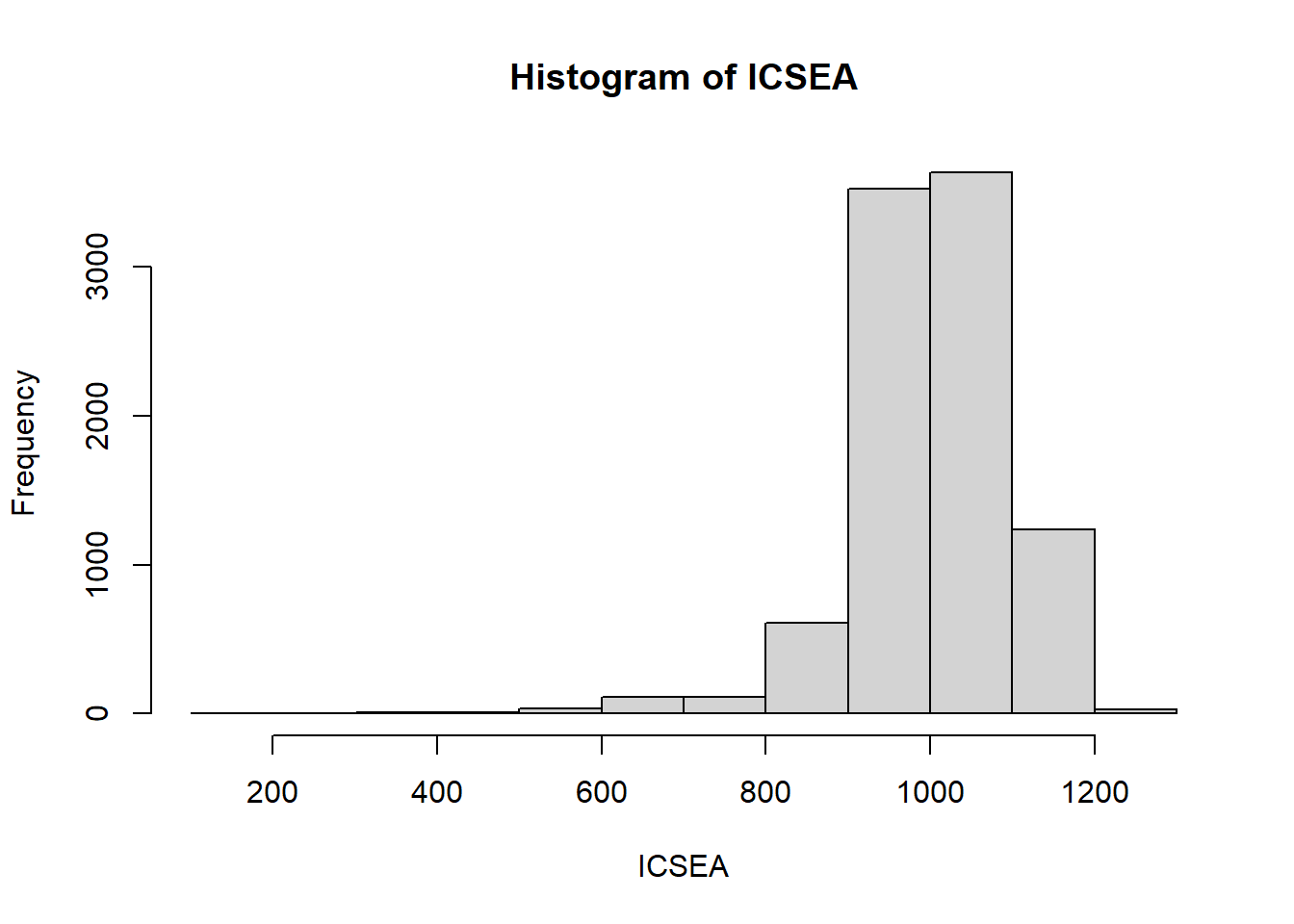

hist(ICSEA, xlab = "ICSEA", proba = TRUE, breaks = 50, col = 'lightblue')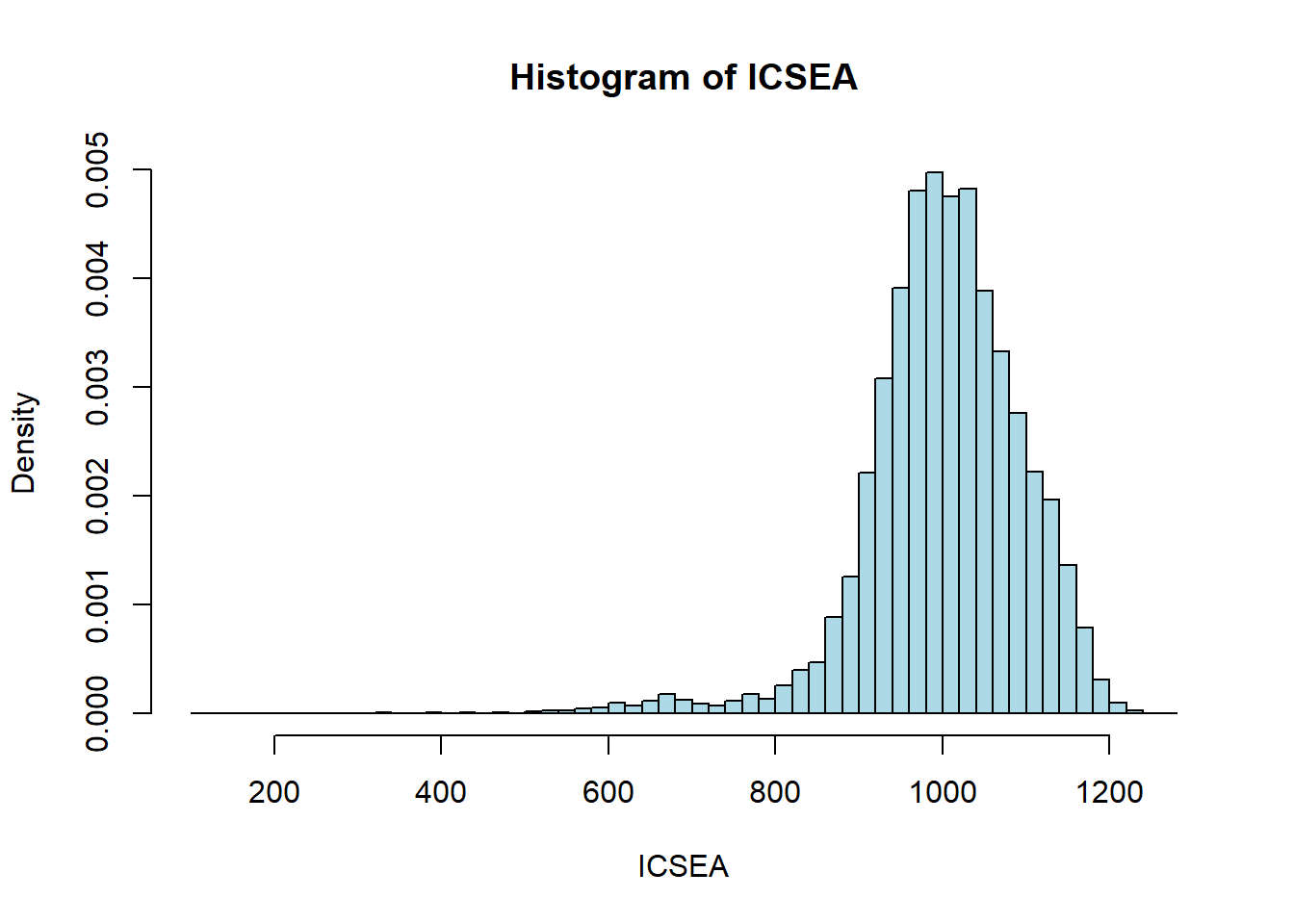

Boxplot

  • A box plot provides a graphical summary of your data, and allows you to quickly compare different groups
  • Each boxplot includes the following statistics: Q1(25% quantile), median, Q3(75% quantile), smallest observation (if bigger than Q1 - 1.5 IQR) and biggest observation (if smaller than Q3 + 1.5 IQR),
  • It gives an idea of both the location and spread of the observations.
boxplot(decrease ~ treatment, data = OrchardSprays, col = "brown3")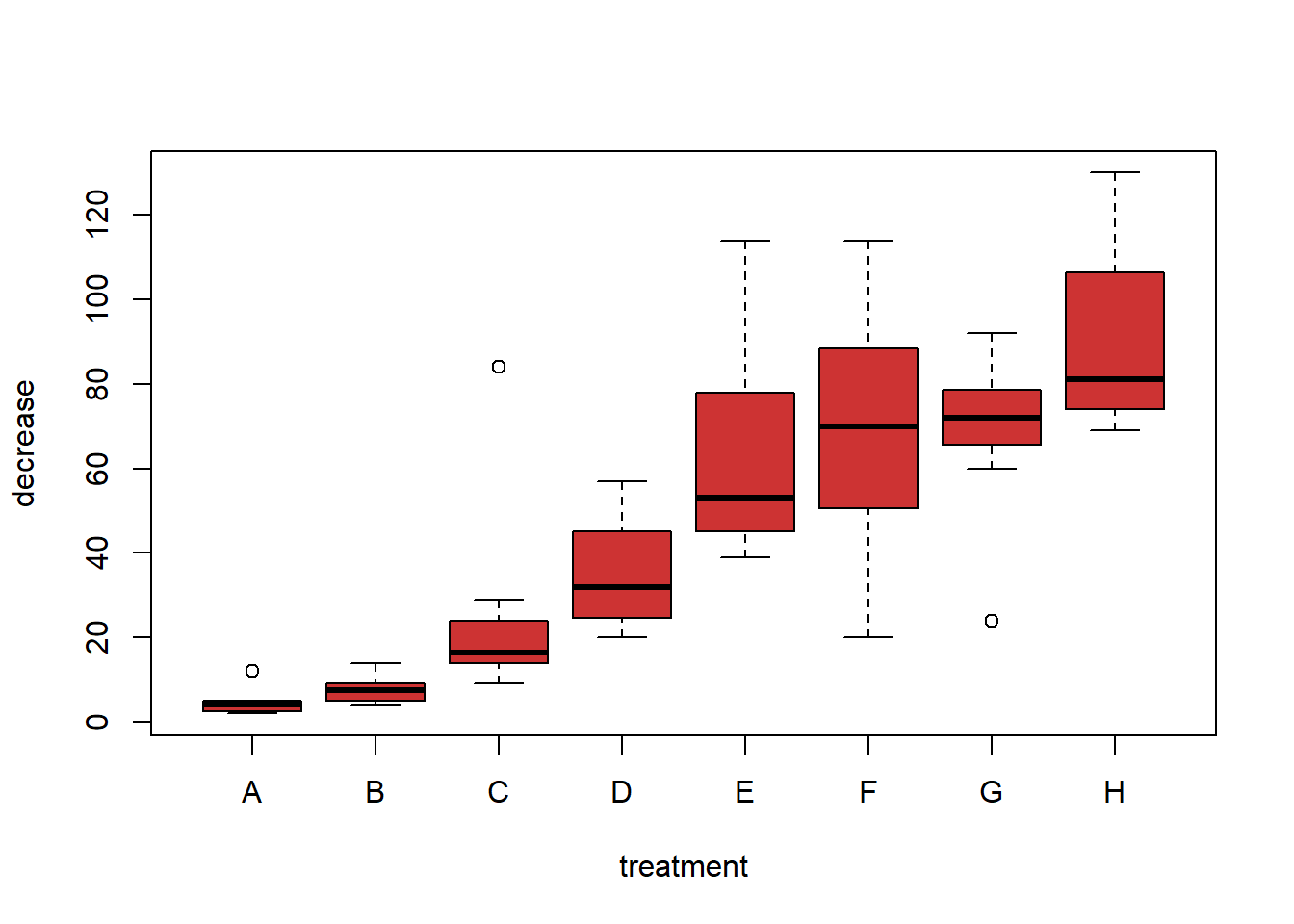

We will not delve far into this y ~ x notation in ACTL1101, but you will see more of it in later courses. It is a way of representing formulae for R functions.

Pie chart, Bar Plot - Pages 358,362

my.col <- c('lightblue', 'lightgreen', 'brown3', 'purple1', 'lightgoldenrod1', 'pink', 'azure4', 'orange')
pie(table(school_data$State), col = my.col, cex = 1.75, main = 'Number of schools by state')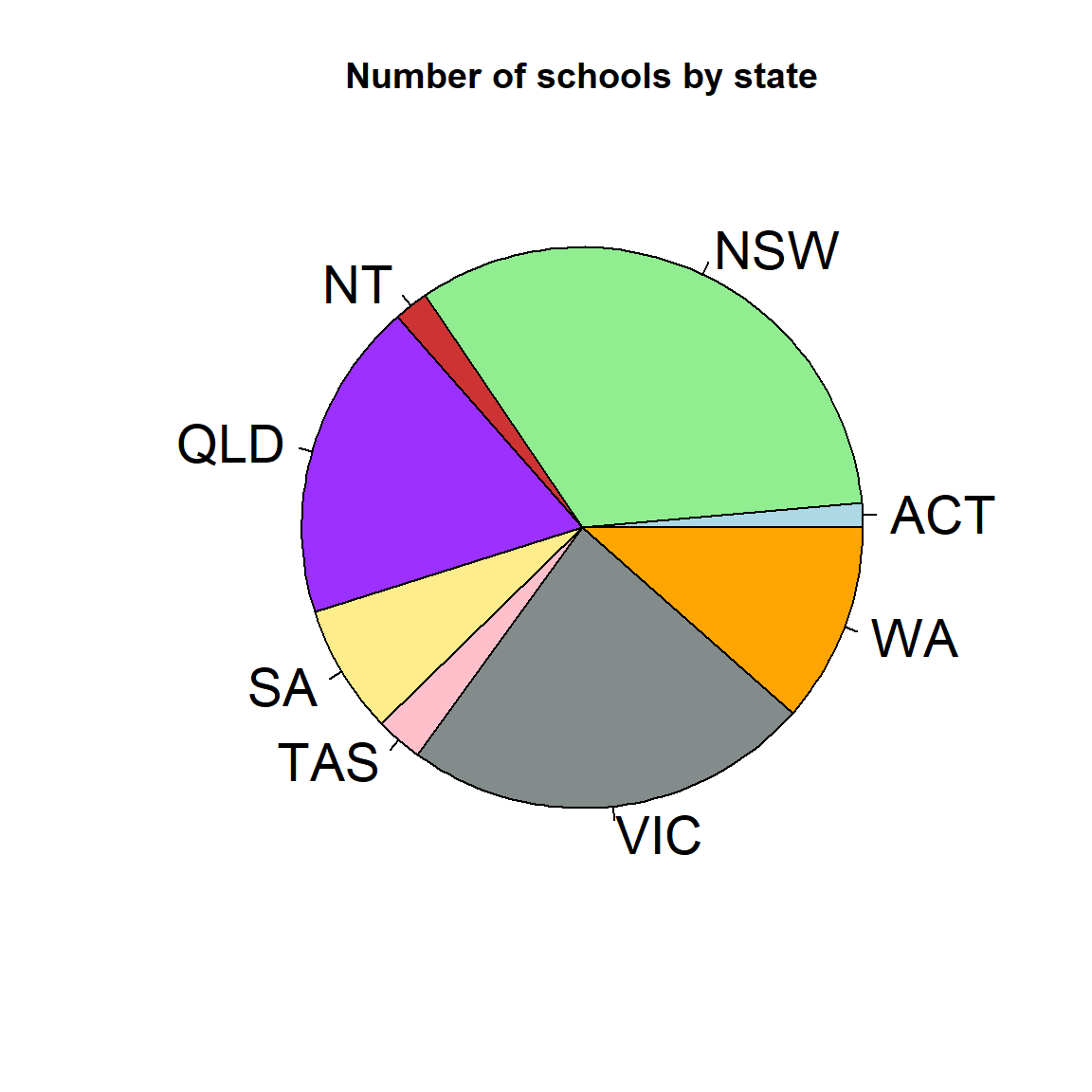

While pie plots are possible in R, you will find many people object very strongly to them. As always however, it comes down to the message you are trying to convey.

barplot(table(school_data$State), col = my.col, xlab = 'state', ylab = '# of schools')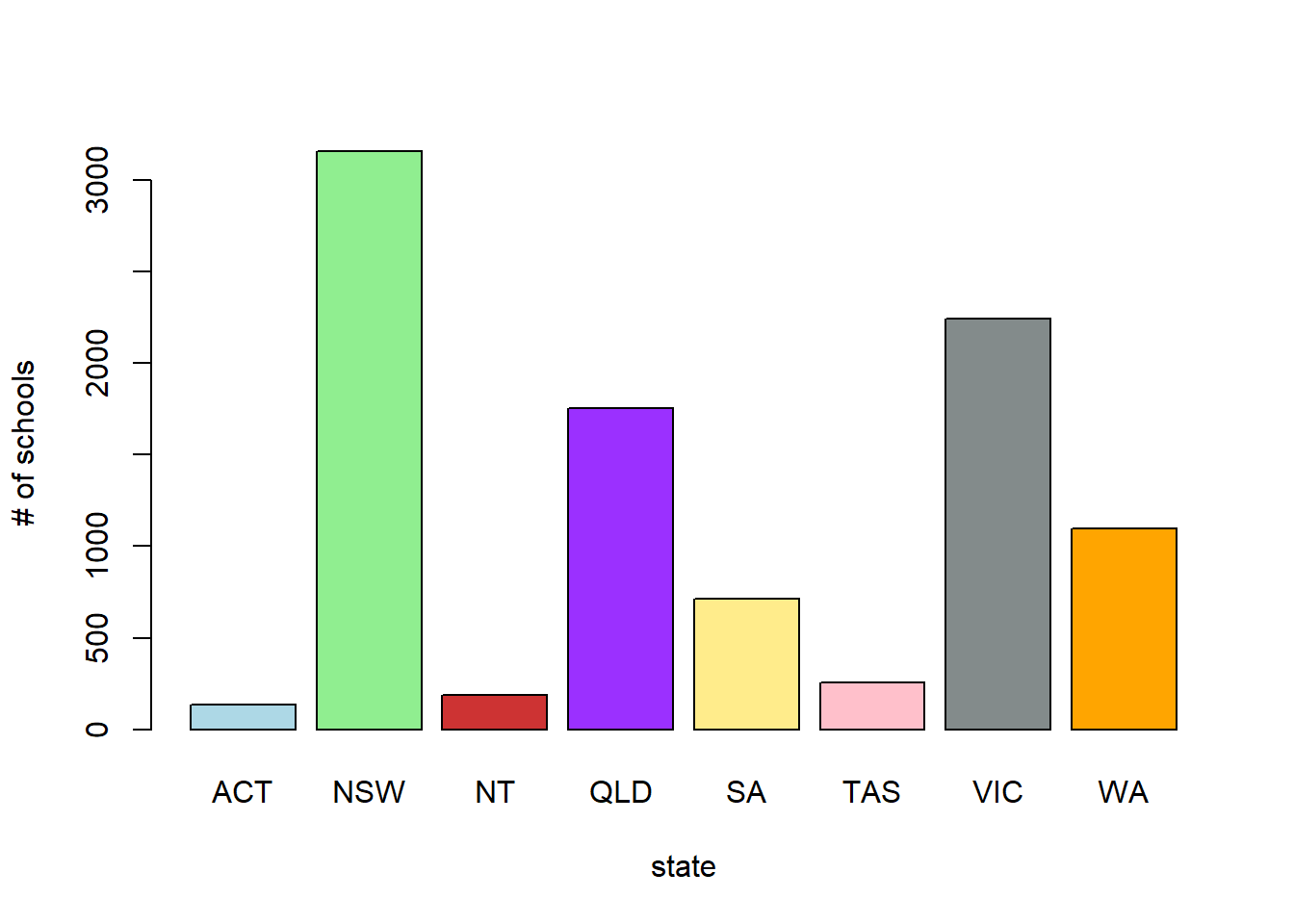

barplot(prop.table(table(school_data$State)), col = my.col, xlab = 'state', ylab = '% of schools')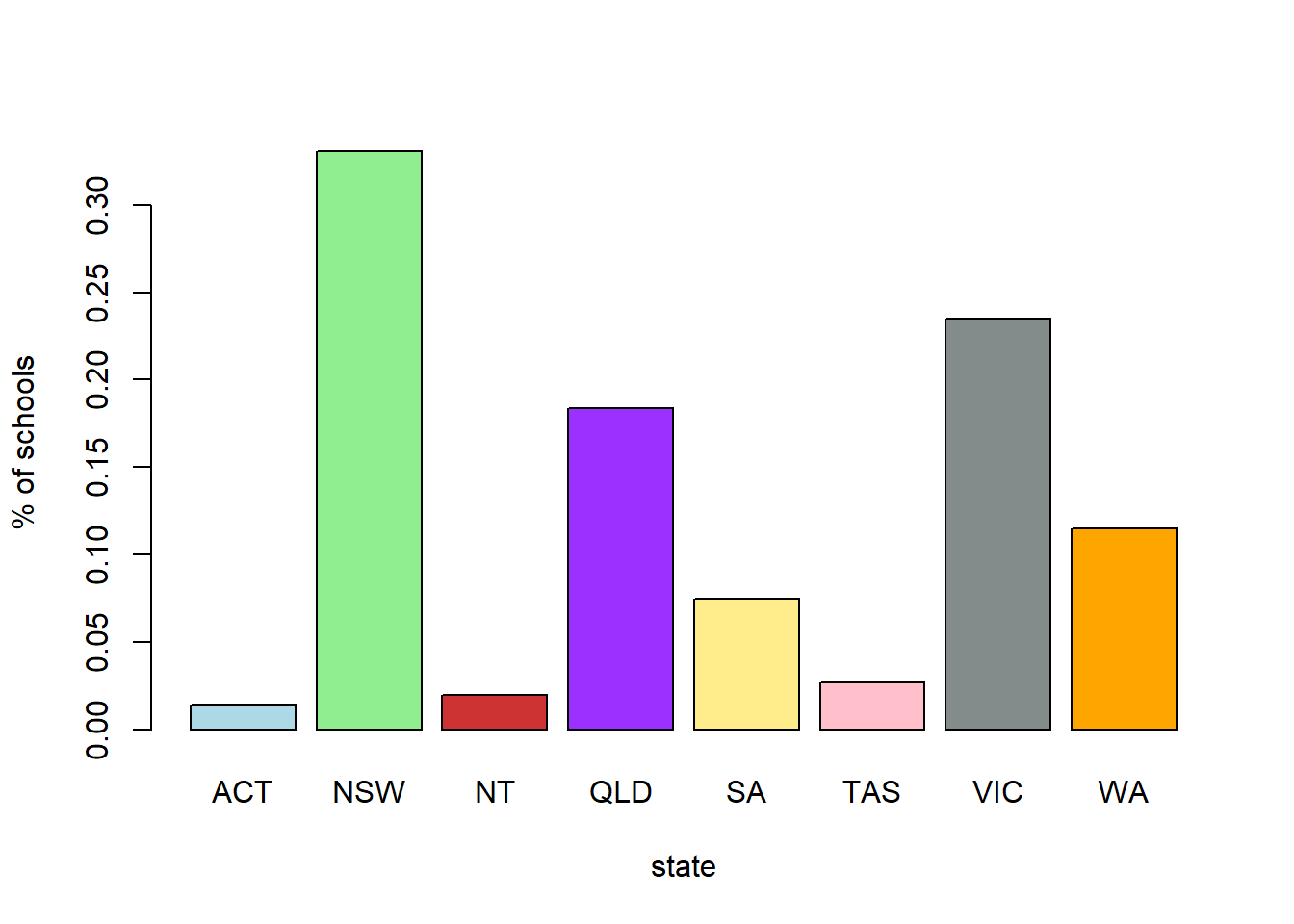

Bar Plot (two categories) - Pages 371-372

  • You can display two qualitative variables with a bar plot… but careful how you do this, different options display very different things!
  • Let’s see examples for variables ‘State’ and ‘School.Sector’
  • Note we play with arguments xlim or ylim to leave enough space for the legend
# We create proportion tables (which are often more useful than raw numbers)
sector.by.state2 <- prop.table(table(School.Sector, State), margin = 2)
sector.by.state1 <- prop.table(table(School.Sector, State), margin = 1)
state.by.sector2 <- prop.table(table(State, School.Sector), margin = 2)
state.by.sector1 <- prop.table(table(State, School.Sector), margin = 1)

barplot(sector.by.state2, bes=T, legend = T, col = my.col[1:3], ylim = c(0,0.95))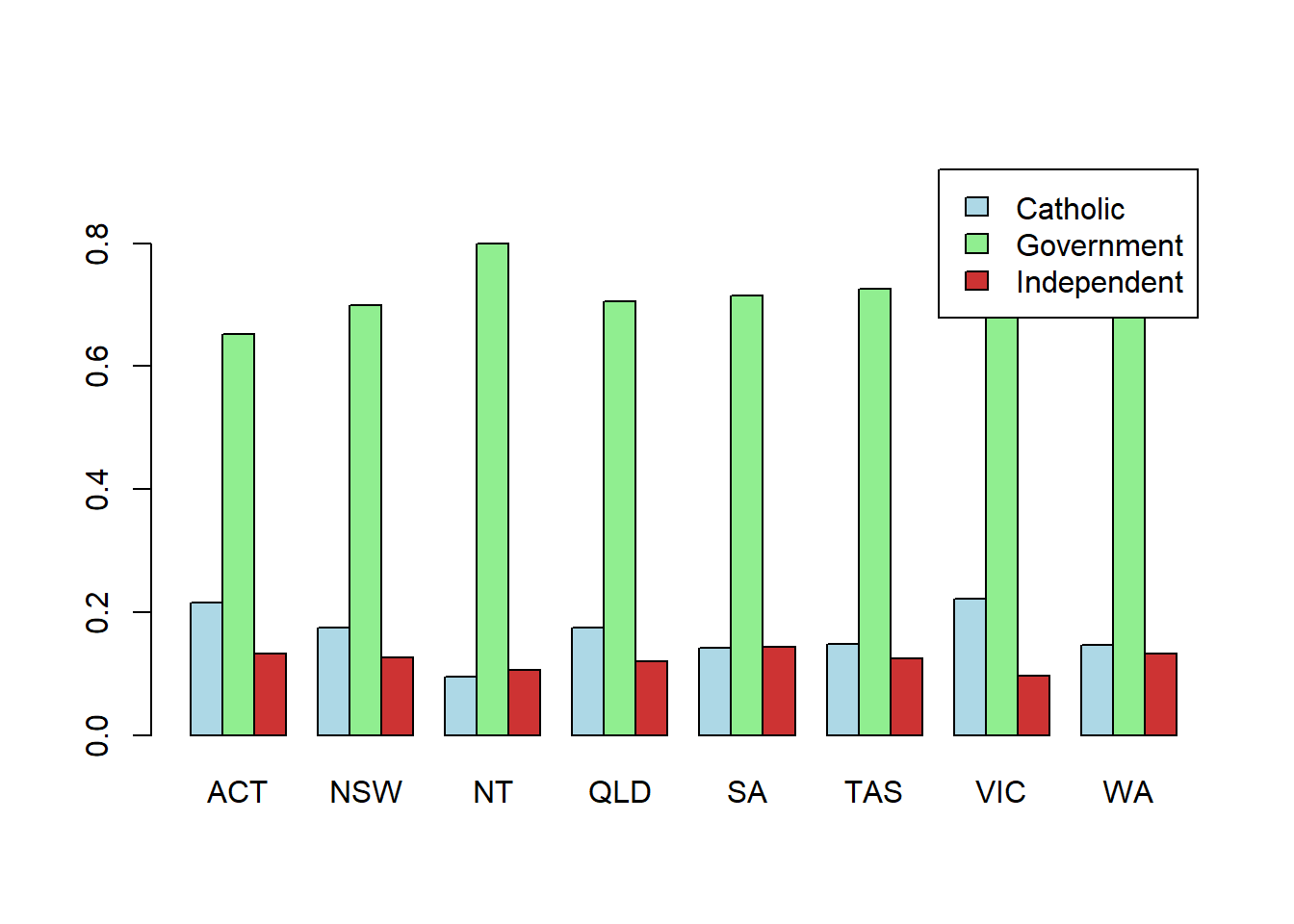

barplot(sector.by.state1, bes=T, legend = T, col = my.col[1:3], xlim = c(0,35))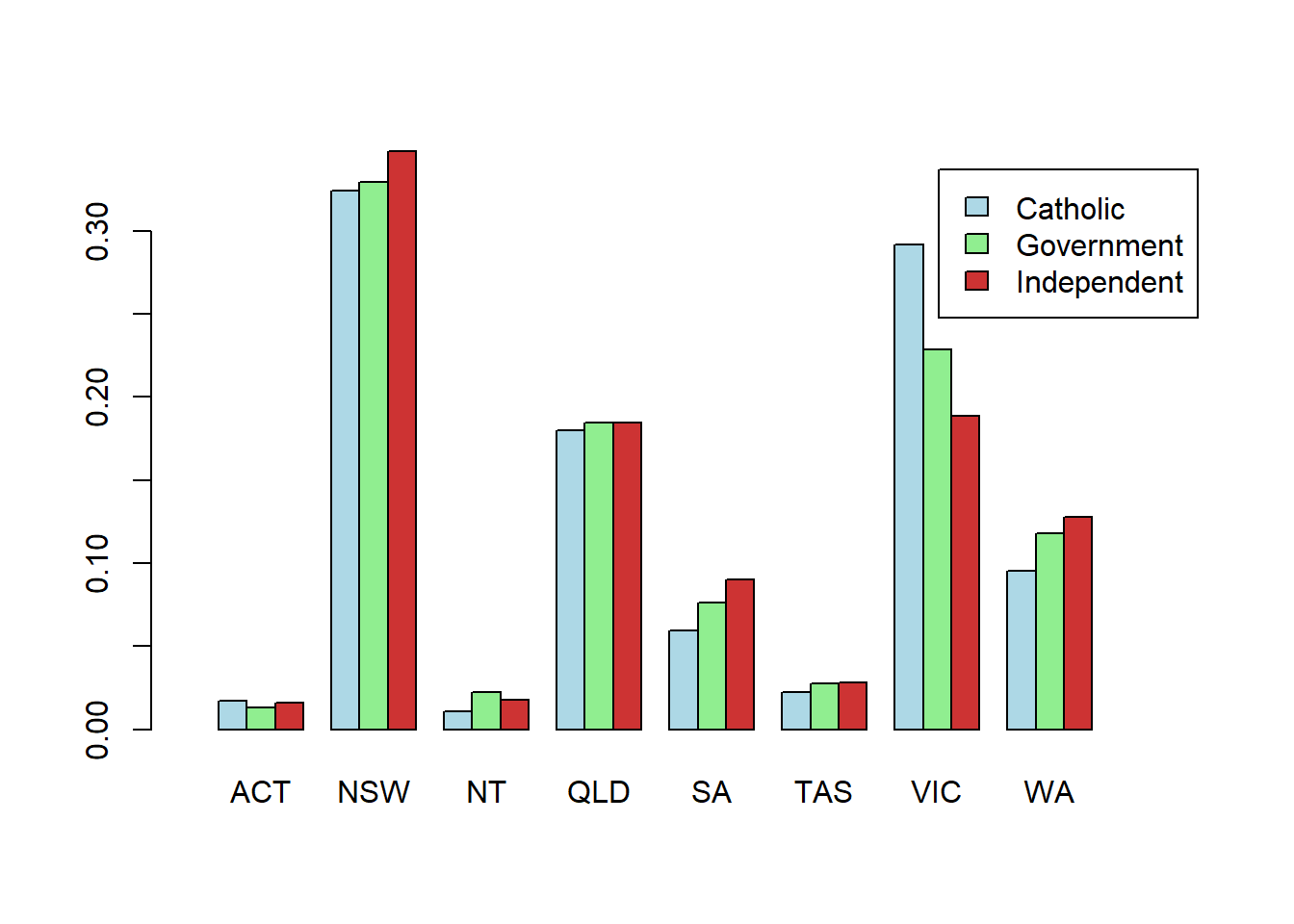

barplot(state.by.sector2, bes=T, legend = T, col = my.col[1:8], ylim = c(0,0.4))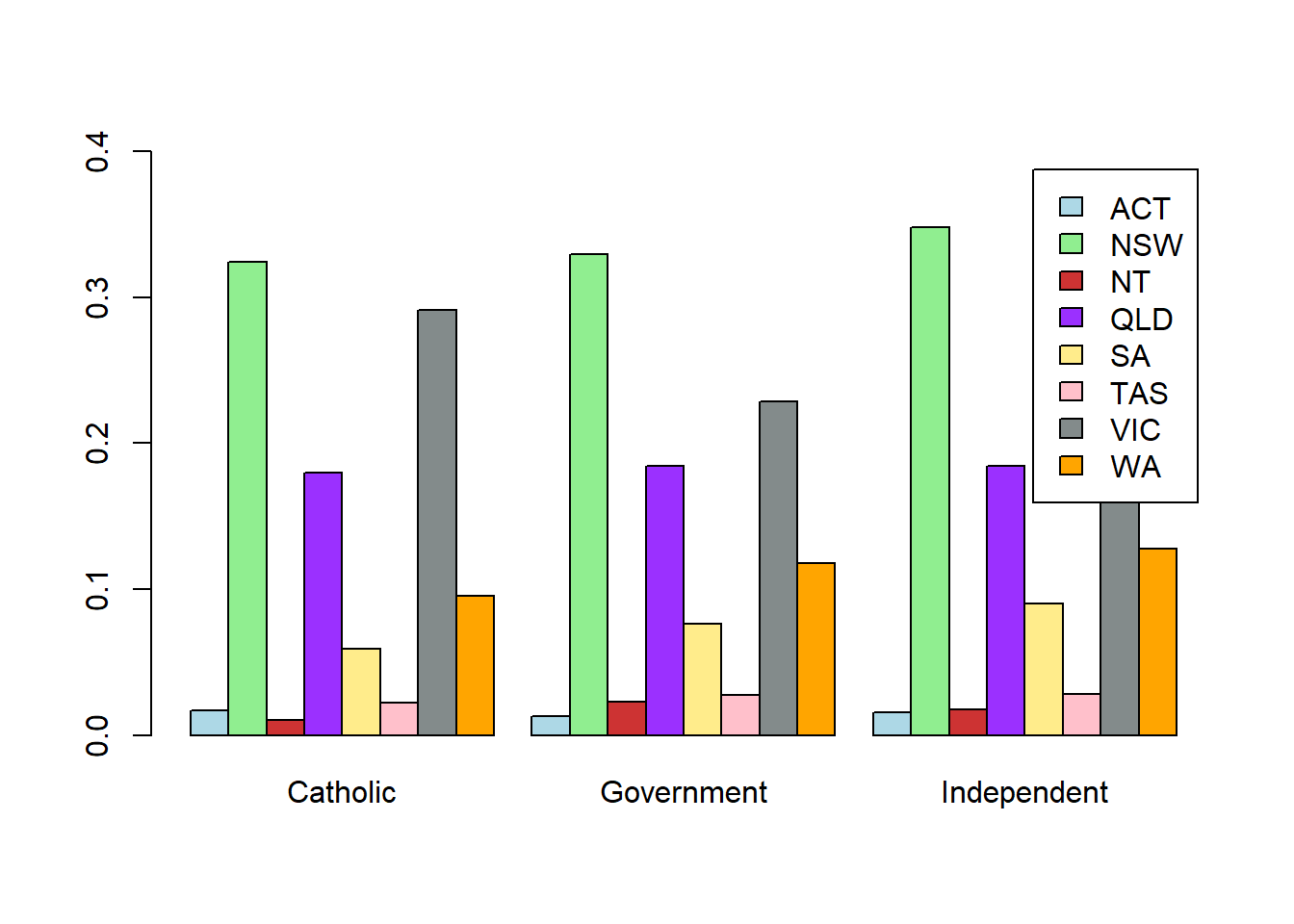

barplot(state.by.sector1, bes=T, legend = T, col = my.col[1:8])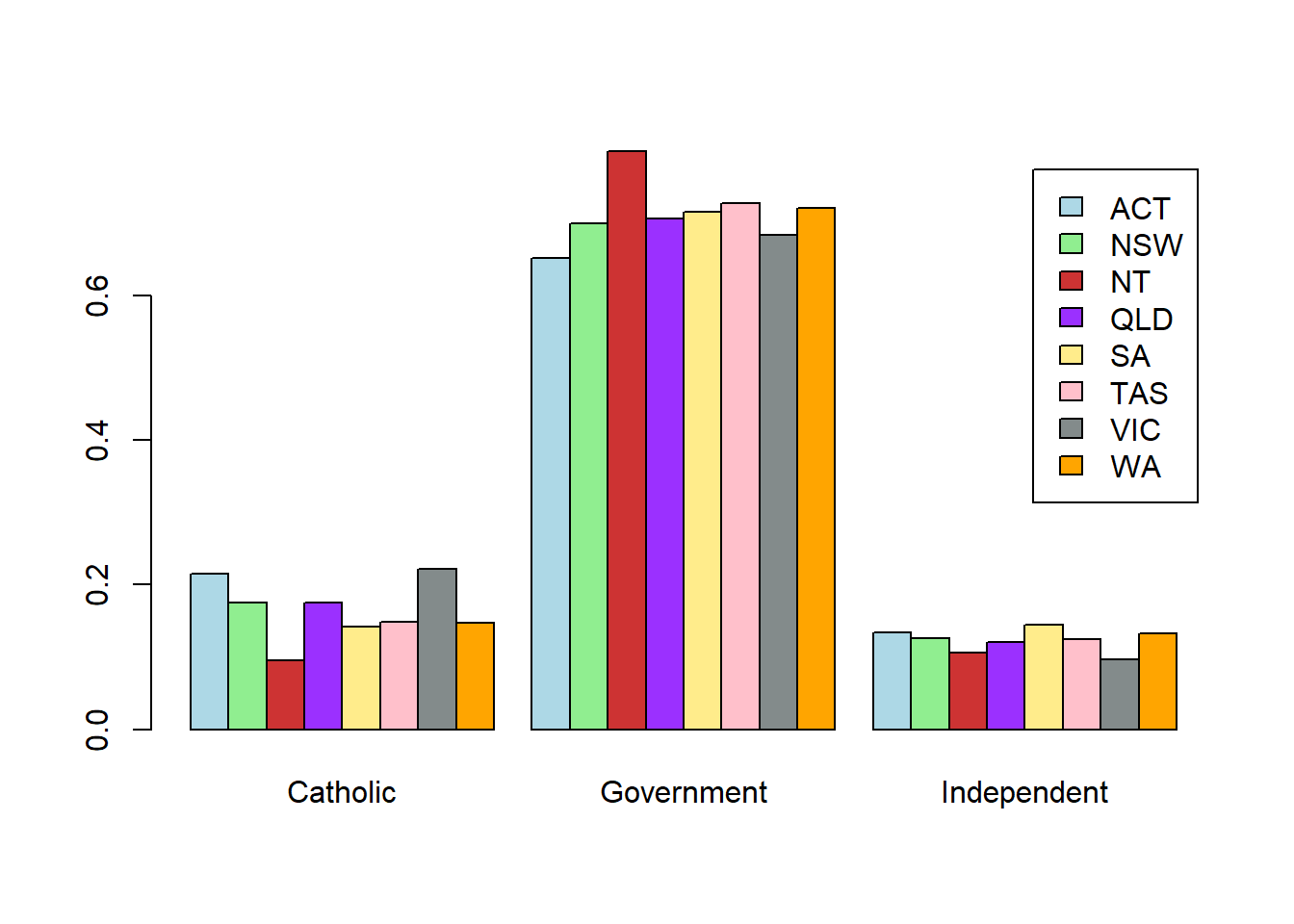

# stacked bars
barplot(sector.by.state2, bes=F, legend = T, col = my.col[1:3], xlim = c(0,13))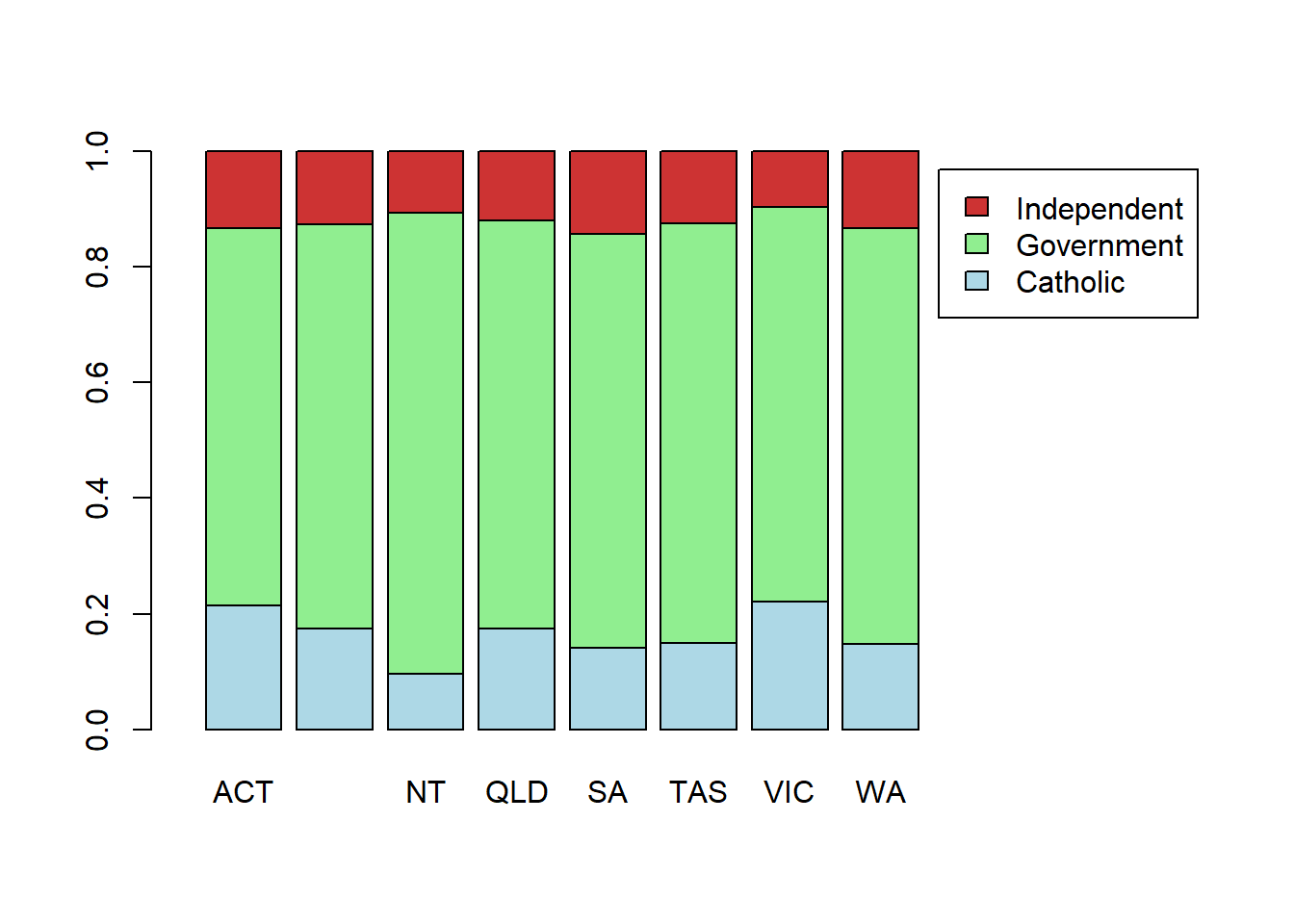

The curve() function - Pages 162

  • To graph a curve (given by a function of x) on the interval specified by the bounds from and to
curve(dnorm(x, 0, 1/5), from=-2, to=2, lwd = 2)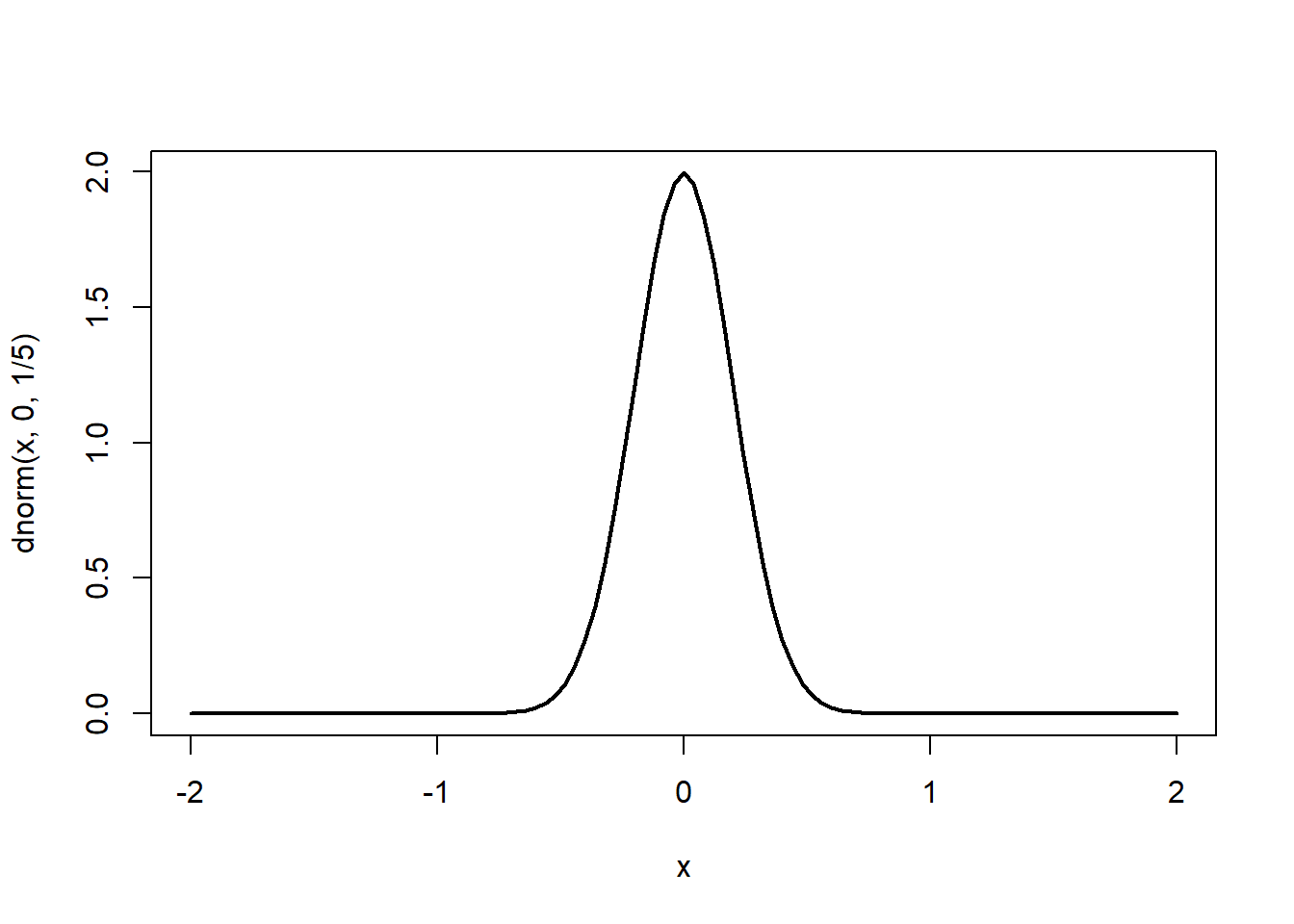

curve(x*sin(1/x), from =-1/10, to=1/10, lwd = 2)
Warning in sin(1/x): NaNs produced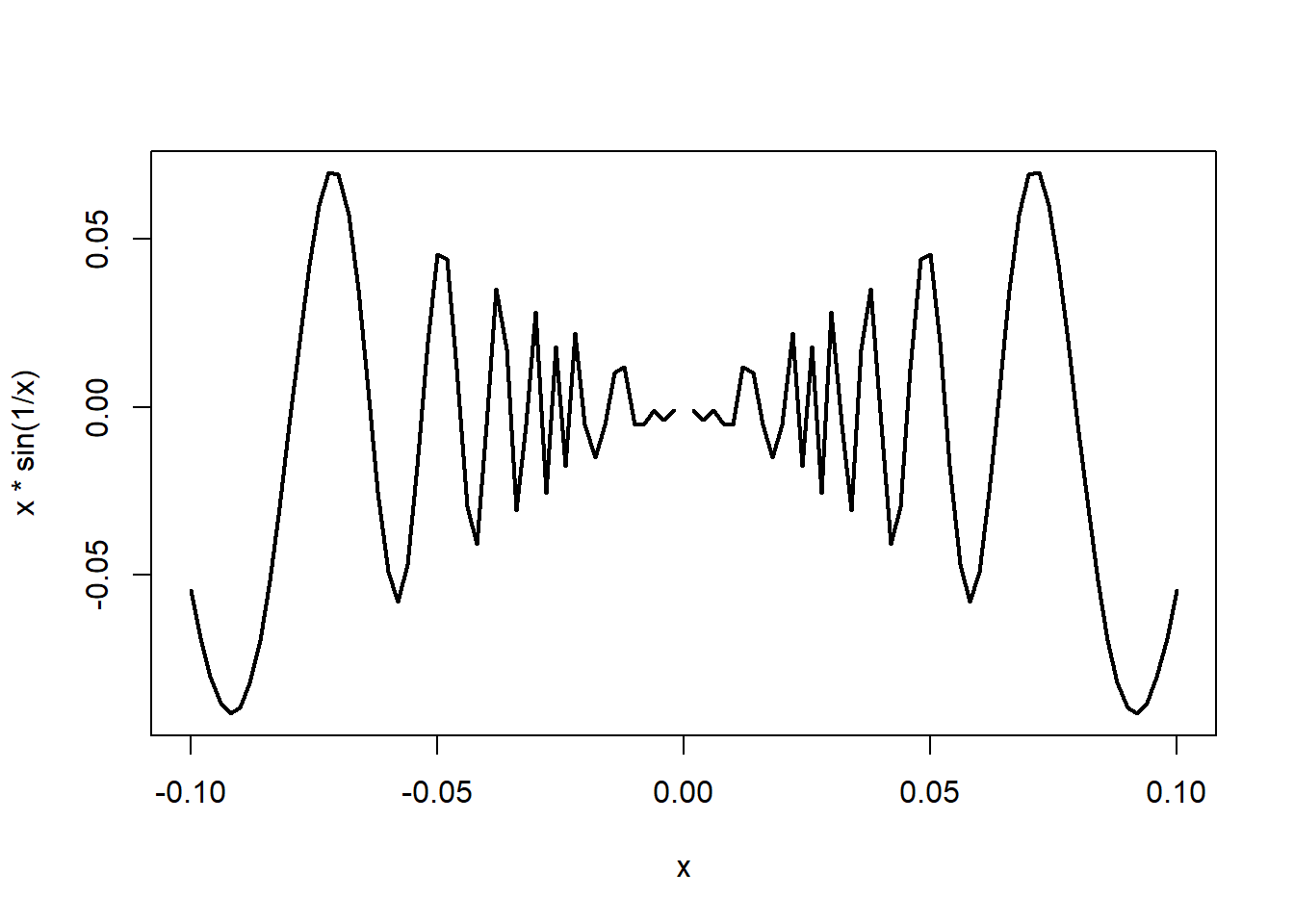

  • The previous plot does not look very good: it is too ‘rough’. This has a quick fix!
# with n=500 we raise the # of points at which the function is evaluated (better resolution)
# with cex.lab=2 we make the axis label bigger with  
# with par(mar=c(5,5,2,2)) we change the margins of the graph 
# the default is c(5.1, 4.1, 4.1, 2.1) (order: bottom, left, top, and right)
par(mar=c(5,5,2,2))
curve(x*sin(1/x), from =-1/10, to=1/10, col = 'brown3', lwd = 1, n = 500, cex.lab = 2)

  • Note also the use of argument lwd (makes the lines wider if larger).

Graphical windows - Splitting the Graphics Window - Page 154

You can easily have several plots (of possibly different types) in one plot, as below.

# Split the window to have 3 lines and 2 columns of plots (to be filled by column)
par(mfcol=c(3,2))
# First plot
plot(1:3,1:3,col="red",type="l", xlab= "", ylab= "")    
plot(1:5,1:5,col="orange",type="p", xlab= "", ylab= "") 
plot(1:7,1:7,col="blue",type="b", xlab= "", ylab= "")   
plot(ts(rnorm(100)),col="purple", xlab= "", ylab= "")
curve(sqrt(x^2 - x^4), from = -1, to = 1, lwd = 2, xlab= "", ylab= "")
hist(rexp(100,1/2), main = "", xlab= "", ylab= "")

Visualisation: but wait, there is more !

  • There is much more to learn about visualisation tools. The R Graph Gallery is a great resource with tons of (reproducible) examples.
  • You should also know that the package ggplot2 is very popular (and powerful) to create ‘neat’ visualisations in R. Check out the visualisation below for an example. We will also provide an (optional) introduction to ggplot2 in a separate set of slides.
library('ggplot2')
library('ggExtra')
Warning: package 'ggExtra' was built under R version 4.4.3
g <- ggplot(mpg, aes(cty, hwy)) + 
  geom_count() + 
  geom_smooth(method="lm", se=F) +
  theme_set(theme_bw())
ggMarginal(g, type = "histogram", fill="transparent")
`geom_smooth()` using formula = 'y ~ x'
`geom_smooth()` using formula = 'y ~ x'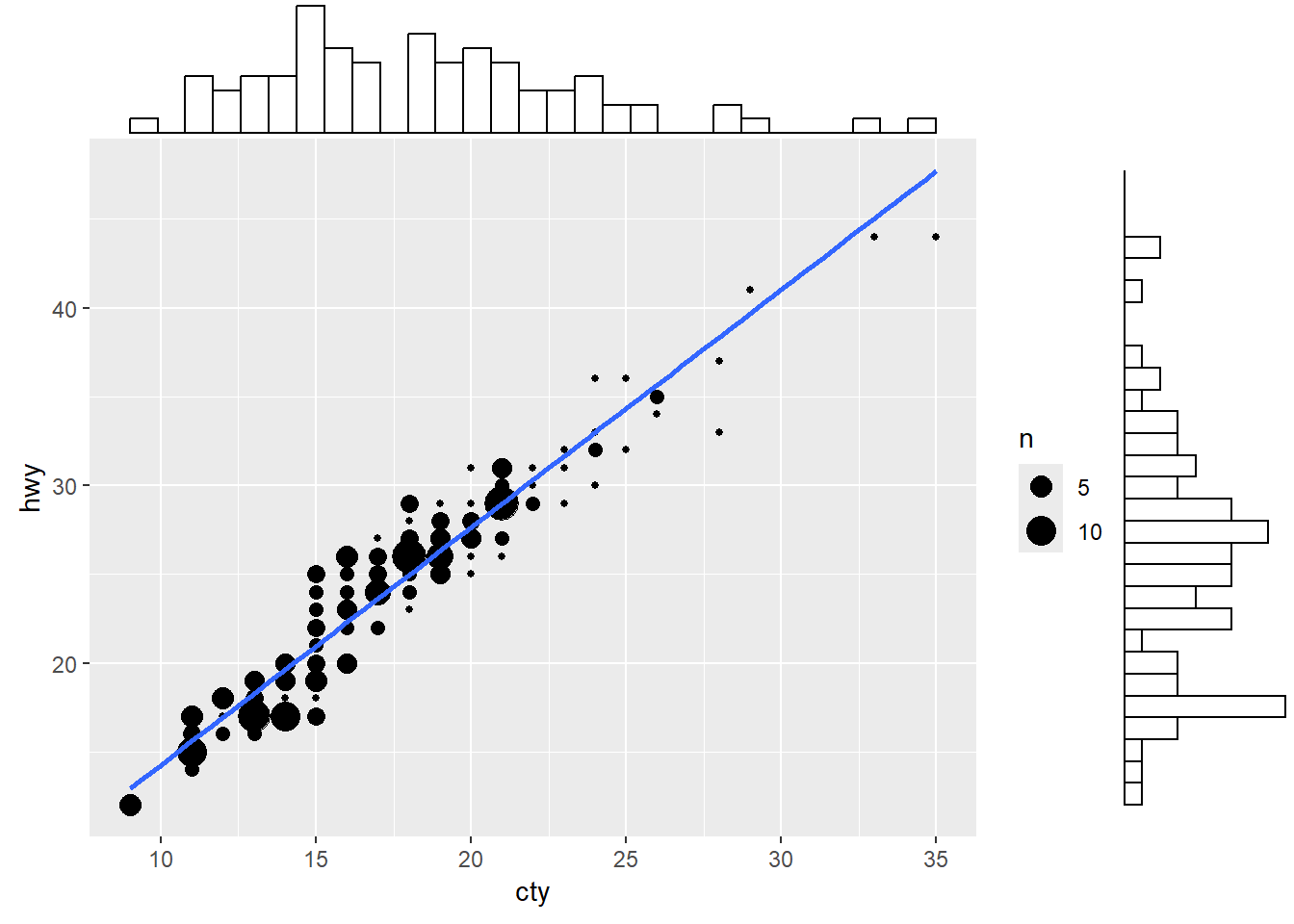

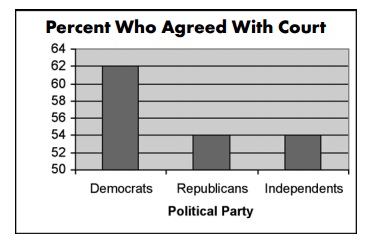
Common mistakes

Common mistakes: Misleading scales of axes

Consider this bar graph showing support for a policy among different groups of voters (USA). At first glance you’d think the difference between Democrats and Republicans is huge… but is it?

Even worse, consider the following chart… can you identify what is odd?

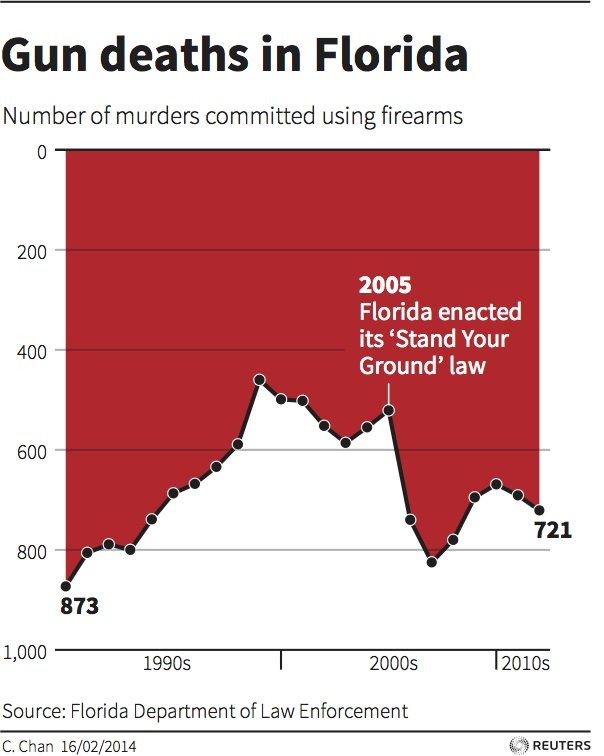
More examples here

Common mistakes: Inapproriate types of graphs

Suppose that you would like to compare the sales of five teams. Is the following graph appropriate?

team.no <- 1:5
sales   <- c(100000,80000,60000,20000,120000)
plot(team.no, sales, type = 'b', lwd = 5, col = 'brown3', 
     xlab = "team number", cex.axis = 1.5, cex.lab = 2)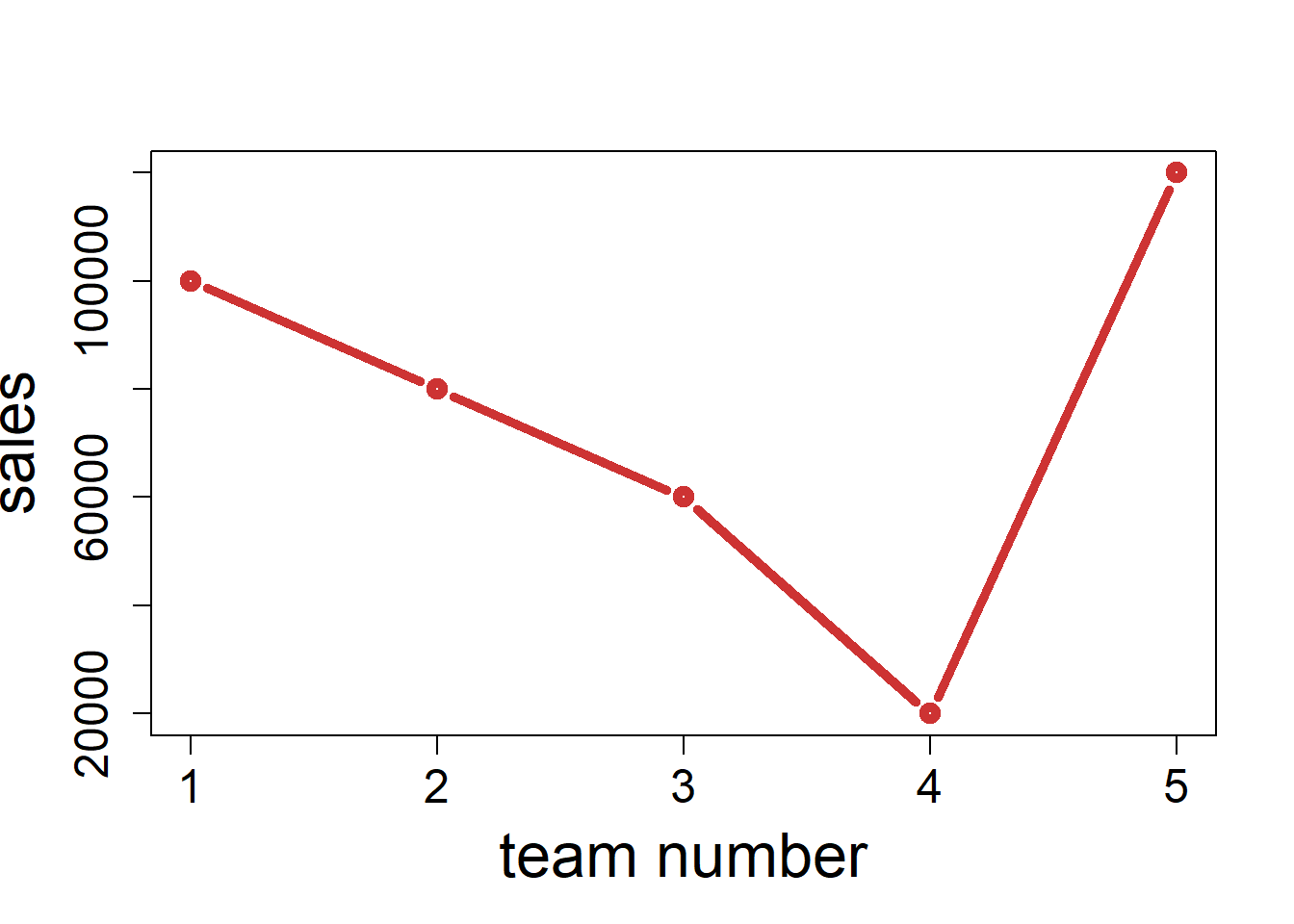

  • Not really! With a line graph, you interpolate between the sales of multiple teams, which makes little sense (for instance, this method seems to assign a value of sales to ‘team 1.5’, but this team does not exist).
  • A bar plot is more appropriate to compare values from distinct groups.
barplot(sales, names.arg = team.no, col = 'chartreuse3', 
        xlab = "team number", cex.axis = 1.5, cex.lab = 2)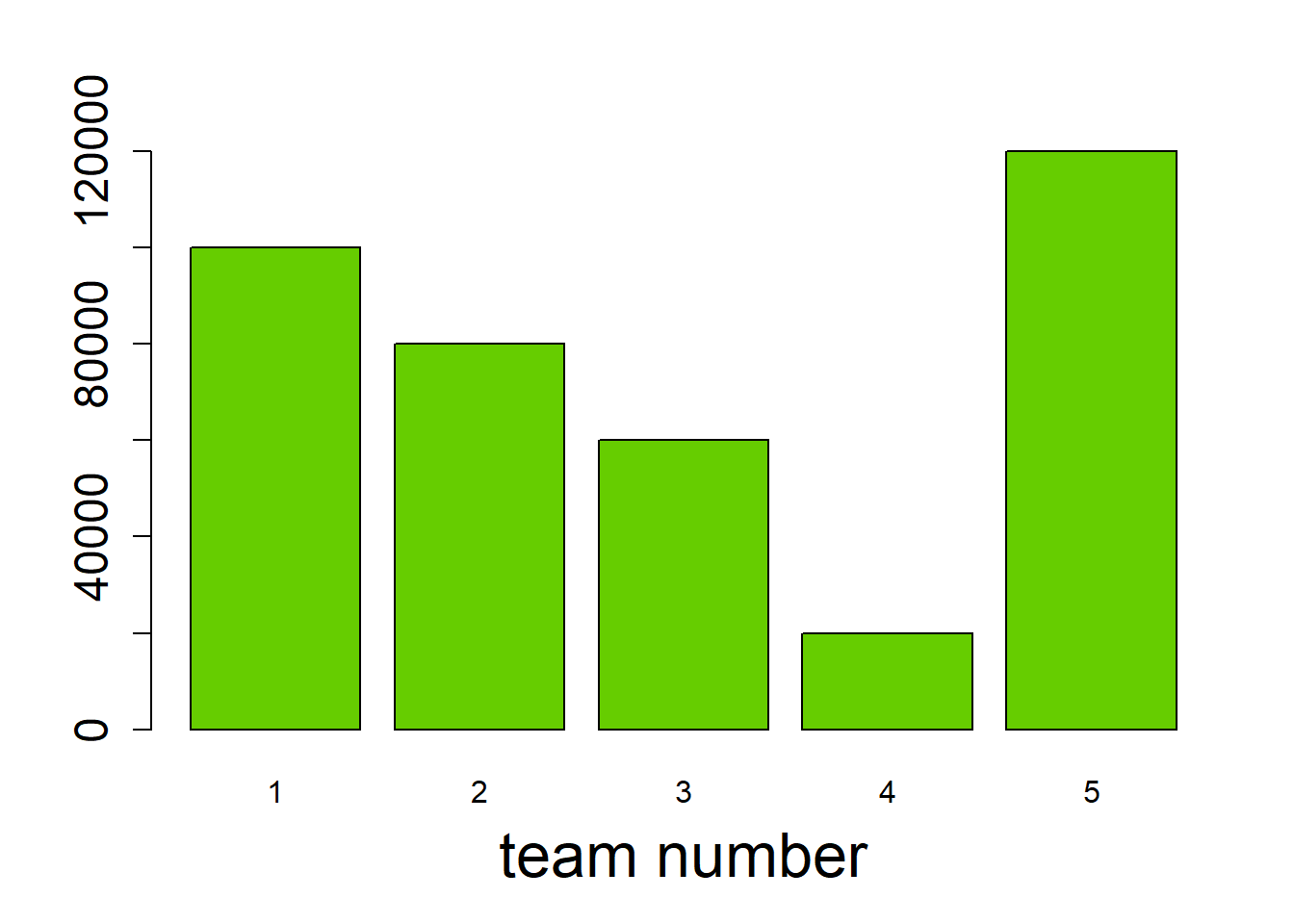

Common mistake: inappropriate scale

  • Here we consider the weight of different mammals’ brain \(y\) (in g) versus their total weight \(x\) (in kg).
  • Because some observations are very large, plotting the ‘raw observations’ produces a scatterplot which is hard to interpret.
  • A common solution is to plot the log() of the observations instead.
  • Do you see how better the visualisation gets with this simple trick?
library(MASS)
plot(mammals$body, mammals$brain)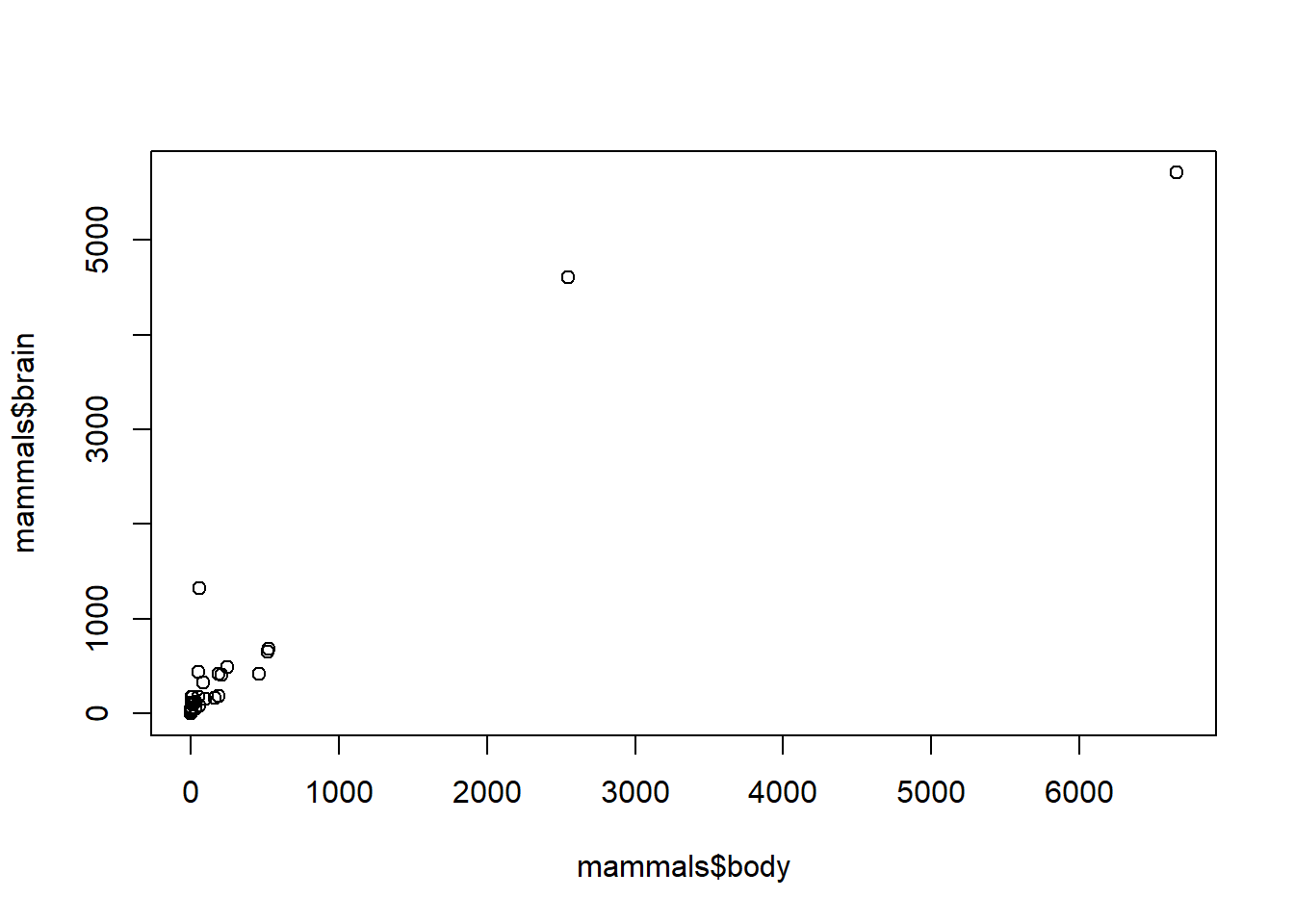

plot(log(mammals$body), log(mammals$brain), 
     xlab = "log of body weight", ylab = "log of brain weight", 
     main = "Brain weight versus body weight of mammals, on a log scale")
abline(lm(log(mammals$brain) ~ log(mammals$body)), col = 'red', lwd = 2)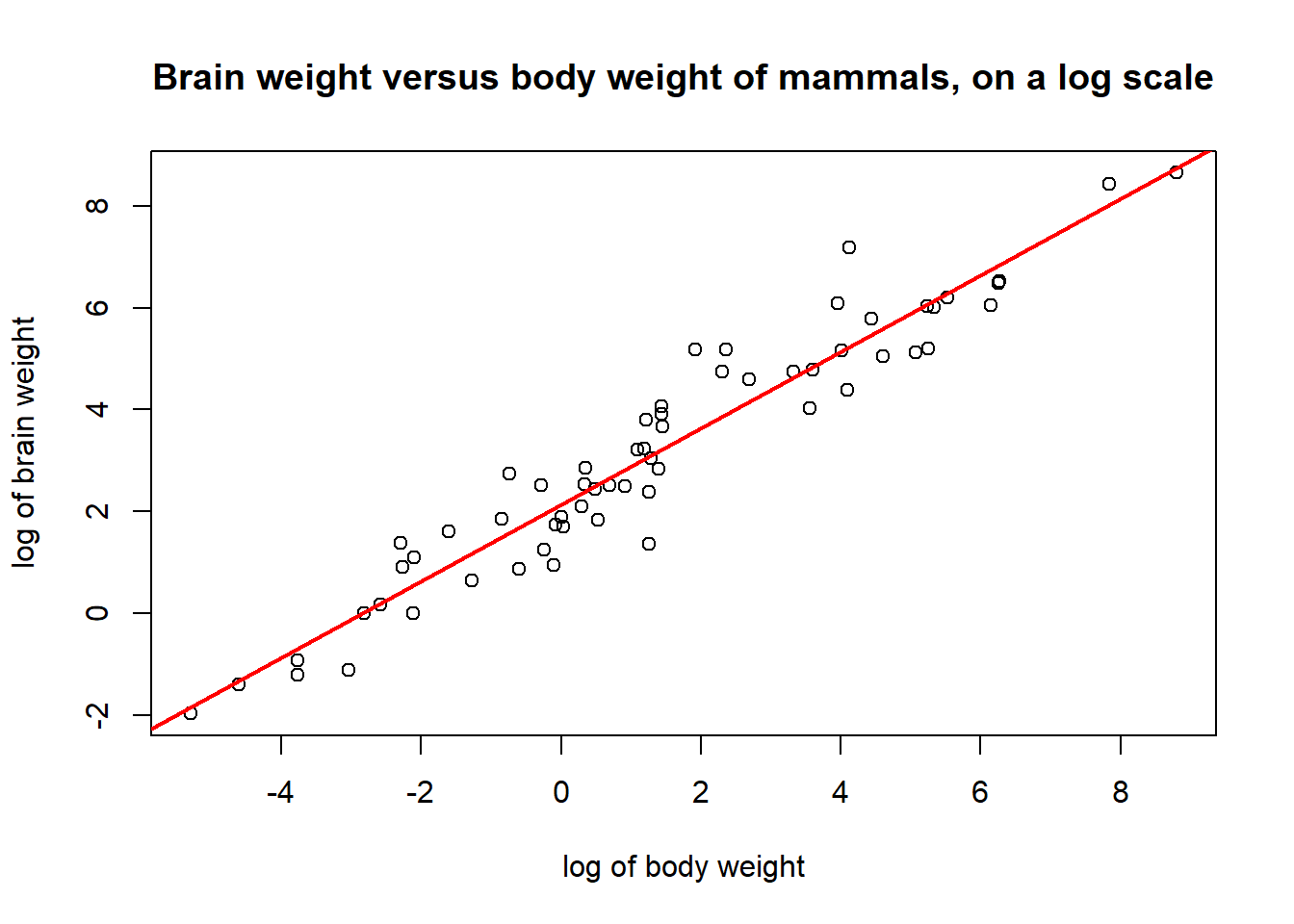

A few general comments on programming

Sad reality: we can’t teach you everything

  • At this point in the course, you have gained familiarity with many “fundamentals” of R and programming in general.

  • You may have noticed (especially this week), that we sometimes don’t explain all the arguments and other specifics of certain functions. This is intentional.

  • A large part of being a proficient coder (and actuary, really) is developing the ability to self-learn new functions and packages and how to complete tasks you never tackled before.

  • Hopefully, you can use the remaining of the term (and beyond) to continue developing your ability to self-learn new R things.

A case study in visualisation

Exercice

  • The ‘Seatbelts’ dataset describes “Road Casualties in Great Britain 1969-84”.
  1. Use the ?Seatbelts command to bring up a description of the data in the help window.
  2. Describe this data set. What sort of insights could we get from analysing / visualising this dataset?

Possible solution

The dataset is a multiple time series, containing the following UK data for each month in the time period 1969-1984:

  • DriversKilled: Car drivers killed
  • drivers: Car drivers killed or seriously injured
  • front: Front-seat passengers killed or seriously injured
  • rear: Rear-seat passengers killed or seriously injured
  • kms: Distance driven
  • PetrolPrice: Petrol price
  • VanKilled: Number of van drivers killed
  • law: Whether seat belts were compulsory (1) or not (0) at a given month.

Solution continued

We could use this dataset to try and answer the following questions:

  • Did the introduction of mandatory seat belts impact the number of driver’s deaths?
  • Does the use of seatbelts affect front-seat and rear-seat passengers differently?
  • Is it riskier to drive a van or a car?

Are there any more interesting trends we could draw from this dataset?

Solution continued

You may have noticed that it was hard to come up with questions without first knowing vaguely what the dataset looks like. Do some exploratory plotting to see what you can find. You should output at least 2 graphs.

[Hint: What is a particularly useful plot type for time series? What are other plot types that give a holistic overview of the data?]

Solution continued

Note that since the data is already a Time-Series data type (Check this using the str() function), the plot() function automatically plots a line graph.

plot(Seatbelts[,'drivers'], ylab = "monthly car drivers killed or seriously injured")

#Add a line to show when seatbelt law was introduced.
#Note here the dates in the x-axis are in decimal format,
#so we manually add line at January  1983 (last month of data with NO seatbelts) 
abline(v=1983.0, col="red")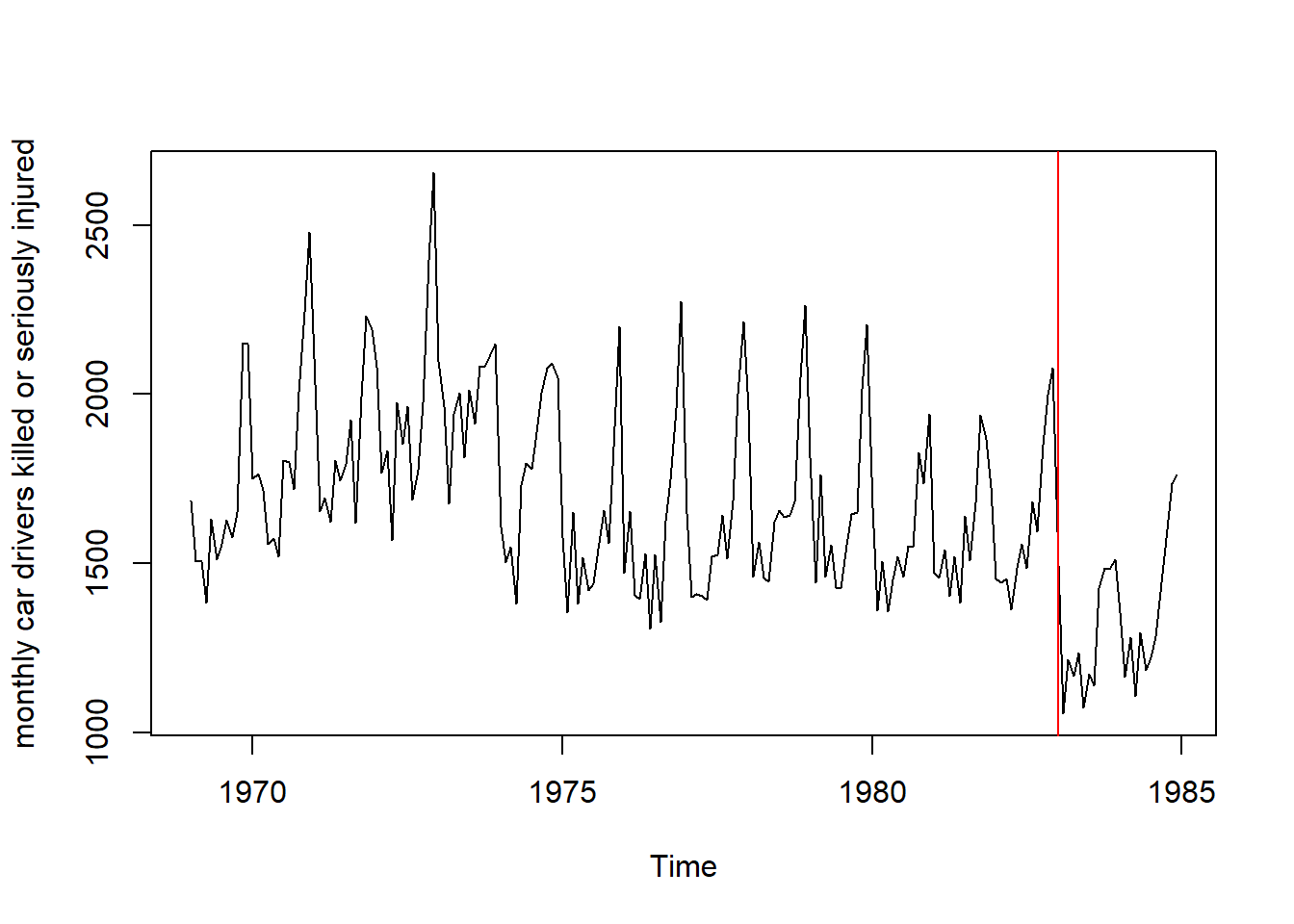

We see that after the introduction of the seatbelt law, there is a distinct drop in driver deaths. We can also see seasonal trends in our data (Why do driver deaths increase during certain months of the year?)

A histogram is also another good graph for general overview. However, note we lose the time aspect of our data.

hist(Seatbelts[,'drivers'], breaks = 30, col = 'lightgreen', xlab = "monthly car drivers killed or seriously injured",
     main="Histogram for UK (Jan 1969 to Dec 1984)")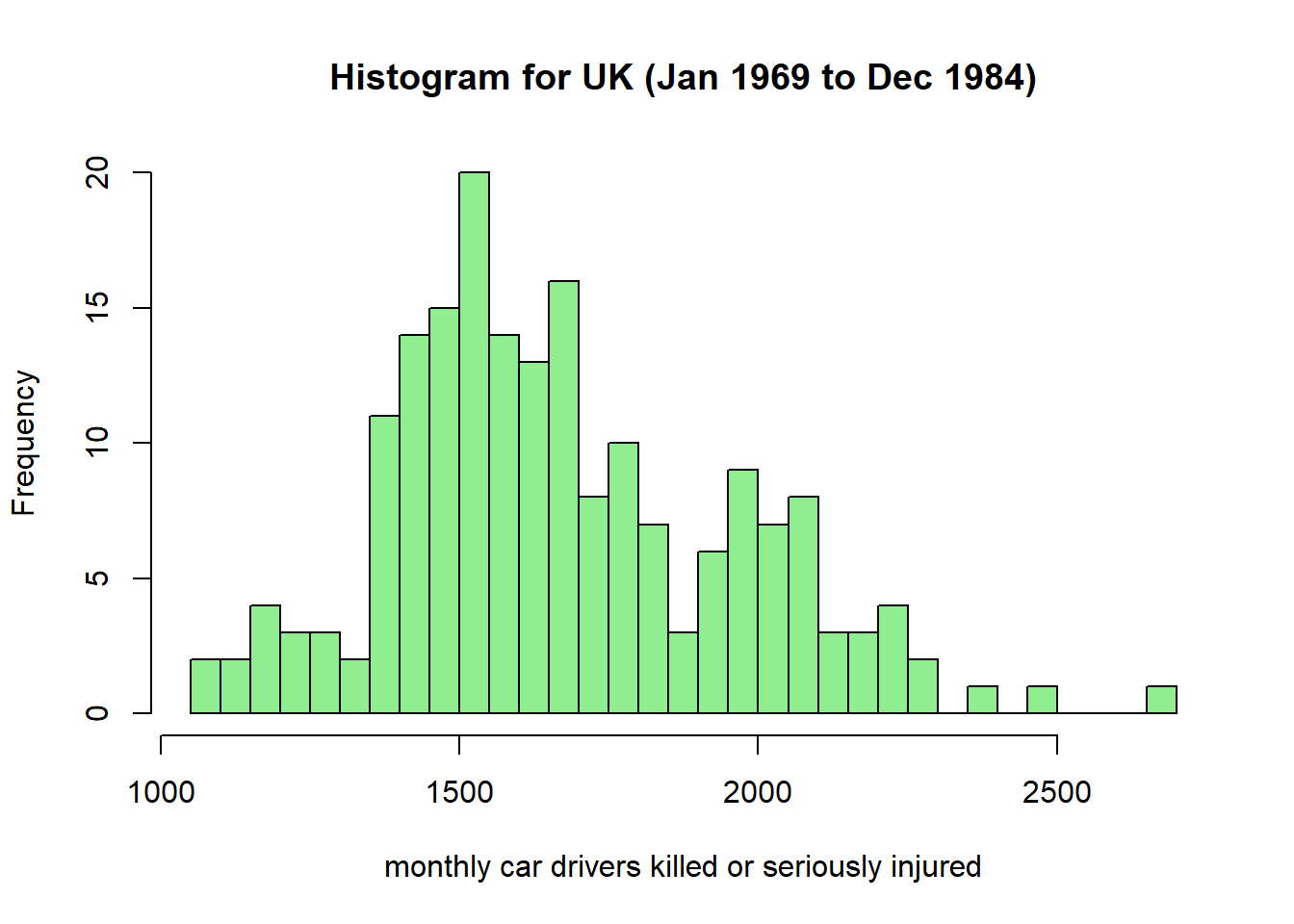

Do you think this distribution can be used for prediction into the future?

Solution continued

Let’s follow the story of the impact of mandatory seatbelt use on the frequency of driver death in the UK. Construct a box plot that compares the distribution of deaths before and after the introduction of the seat belt law.

Discussion

# Boxplots of the two groups (before and after mandatory seatbelts)
boxplot(Seatbelts[,'drivers'] ~ Seatbelts[,'law'], xlab = "Mandatory Seatbelts: NO(0) or YES(1)", 
        ylab = "Deaths & Serious Injuries", col = 'lightblue')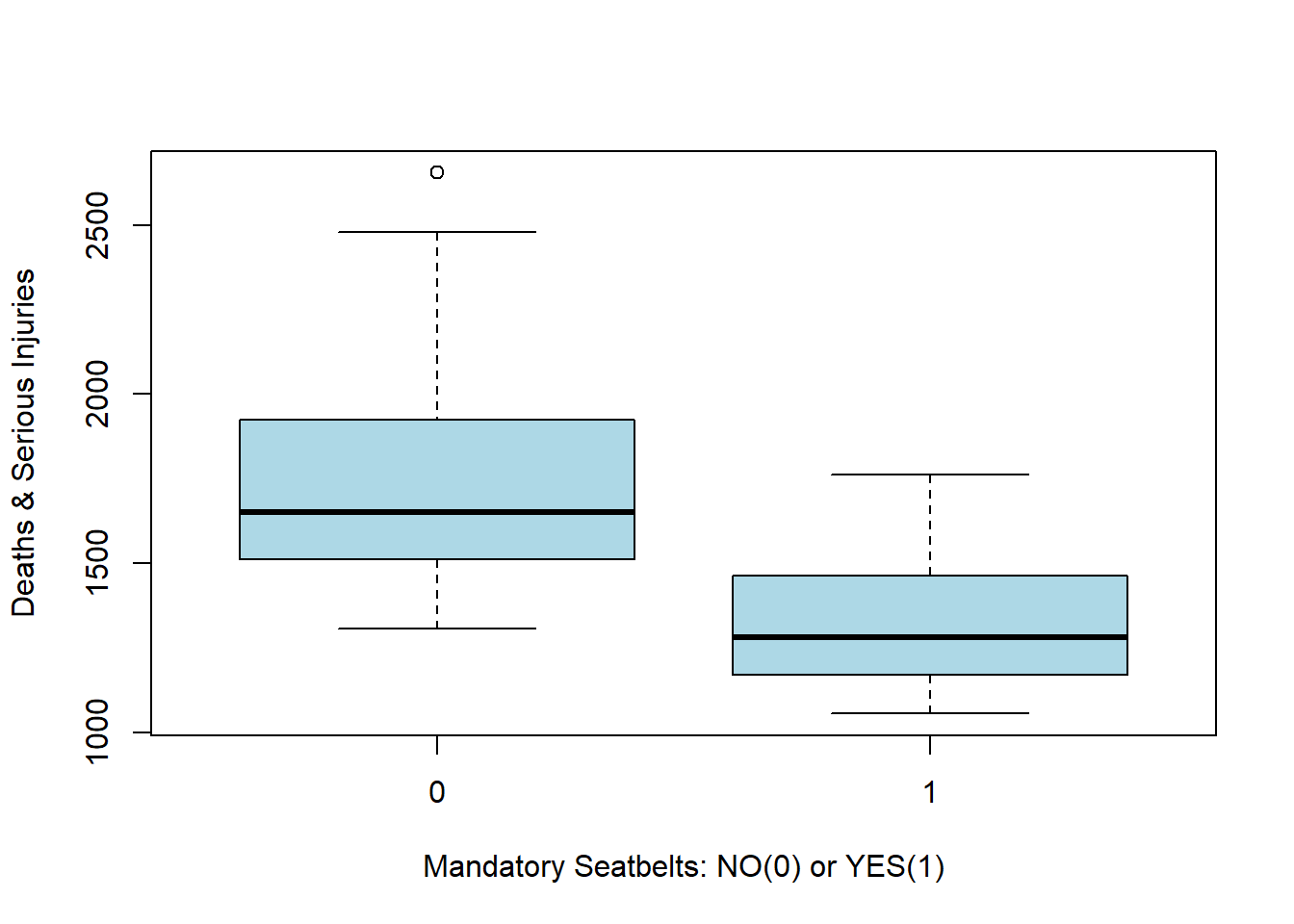

  • Thus it does seem like the seat belt law had a significant effect on driver deaths. But was it statistically significant?

  • We can give an approximate confidence interval on the mean number of deaths (by month), before and after the change in policy using dplyr.

# Note that to use dplyr we need 'Seatbelts' to be a data frame
as.data.frame(Seatbelts) %>% 
group_by(law) %>% 
summarise(mean = mean(drivers), sd = sd(drivers), nb = n()) %>% 
# Add a variable for the lower and upper bounds of a 5% CI
mutate(ci.low = mean - 1.96*sd/sqrt(nb), ci.high = mean + 1.96*sd/sqrt(nb))
# A tibble: 2 × 6
    law  mean    sd    nb ci.low ci.high
  <dbl> <dbl> <dbl> <int>  <dbl>   <dbl>
1     0 1718.  267.   169  1678.   1758.
2     1 1322.  200.    23  1240.   1403.
  • Thinking critically, one might notice that absolute number of deaths is not the best indicator of death likelihood, as the driving population of UK is not constant. You could try and find a source for the driving population of the UK during those time periods. You may have to make certain assumptions such as, the population varies linearly over time (if only yearly data is available) or the driving population is proportional to total population (if driving population is not directly available).

Homework

Homework Exercise 1

Using the mtcars dataset:

  • plot the wt by the mpg for cars with 4 cylinders using a scatter plot
  • add a scatter plot of the wt by the mpg to the pre-existing plot for cars with 6 cylinders
  • repeat the above step for cars with 8 cylinders
  • add a legend to distinguish between the three sets of points

Homework Exercise 2

Use the ‘iris’ dataset. Plot the average ‘Sepal.Length’ for every different ‘Species’.

Hint: dplyr!

Homework Exercise 3

  • Generate two random samples, each of size \(10,\!000\), one stemming from a \(N(-3,1)\), and the other from a \(N(3,1)\) distribution.
  • On the same graph, plot the histograms of the two samples, and with two different colors for the bars of each histogram. Set the argument prob=TRUE. Hint: argument add=TRUE from hist().
  • Use function curve() to add the two curves of the densities (a \(N(-3,1)\) and a \(N(3,1)\)) on top of the histograms.
  • Add a legend.

Homework Exercises 4

This exercise is a continuation of a previous’ week exercise. The dataset motor.df is accesible on Ed. As a reminder, this dataset contains some information about a large number of vehicle insurance claims, by policy. In Ed, the summary dataset summary.df has also been generated for you. Perform the following tasks:

  1. Produce a visualisation of the distribution of variable GrossLossMotor across all policies using the motor.df dataset. What is a possible improvement that could be made to the x axis of this histogram?

  2. Produce another visualisation of the daily numbers of insurance claims from the year 2006 to the year 2015 using the summary.df table. Make sure that this plot:

  • is a time series rather than a scatterplot
  • has an appropriate main title
  • has appropriate labels for the x and y axes

Additional Notes: Adding text - Page 169-170

  • You can add text and mathematical expressions to a plot.
  • Take a careful look at the code and identify which line has added which element.
curve(x*sin(1/x), from =-1/10, to=1/10, lwd = 2, n = 500, col = "darkblue", xlab=expression(theta[i]), ylab=expression(y[i]), cex.lab = 2)
text(0, -0.05, "Fun with R", cex = 1.5, col = "purple")
text(0, 0.05, expression(y==theta*sin(1/theta)))
p <- 4
text(0, -0.075, bquote(beta[.(p)]), cex = 2)
mtext("Marginal text", side=4)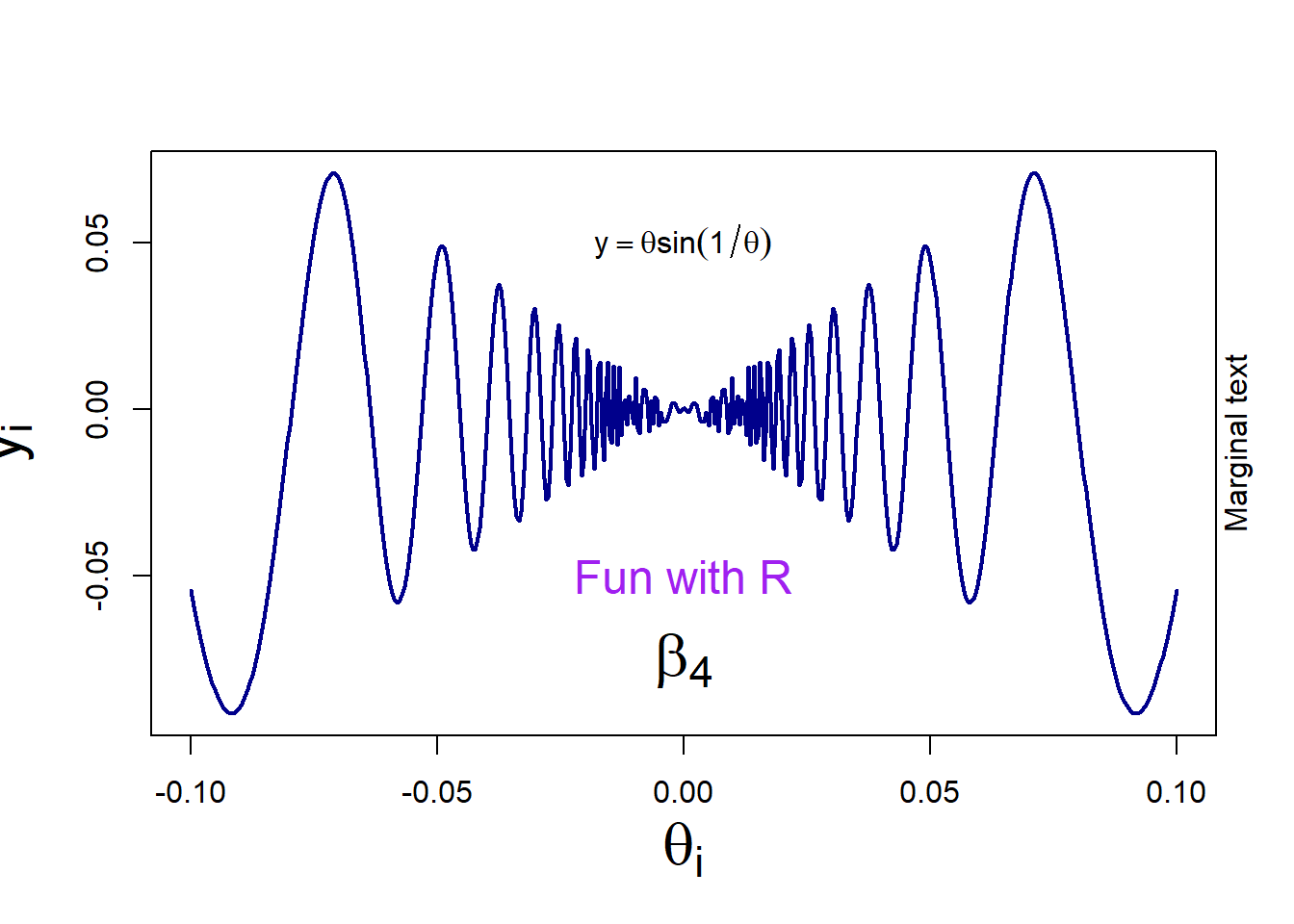

Notes:

  • argument cex allows you to change the size of elements
  • we used a R expression to create math notations
  • bquote is useful when your math expression is dependent on the value of a variable (here the value of p is displayed)

Additional Notes: the segments() and lines() functions - Pages 158-159

To join points with straight lines on an existing plot:

# create an empty plot
plot(0,0,"n", xlab="", ylab="") 
# add a segment joining two points
segments(x0=-0.5, y0=0, x1=1, y1=-0.5, col = "red", lwd = 4)
# add two segments, joining three points: first argument is the 'x' values, second is the 'y' values
lines(c(-1,0,1), c(-1,0.2,1), col = "blue", lwd = 4)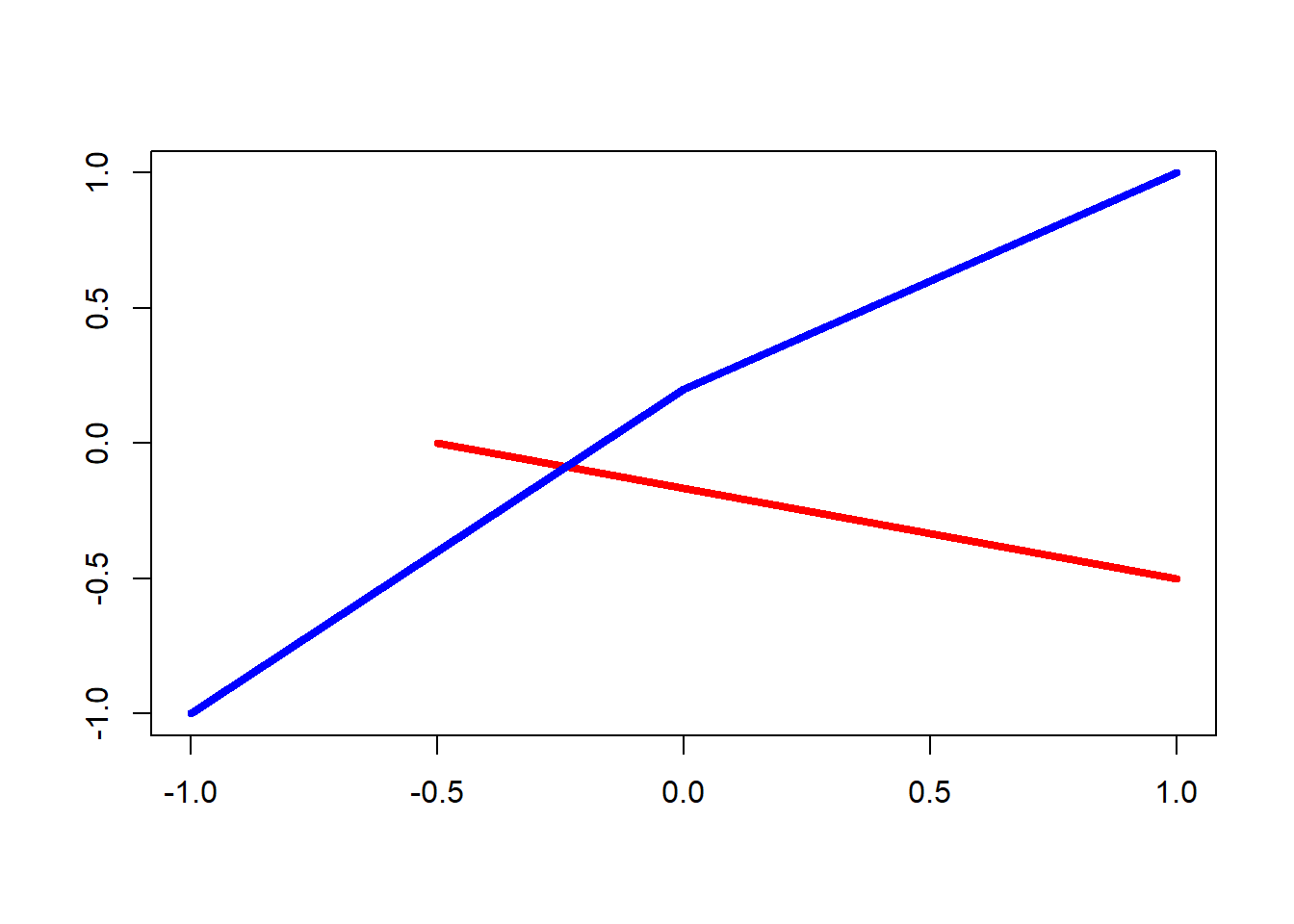

Additional Notes: the abline() function - Pages 159

To draw a straight line of equation \(y=a+bx\) (specified by the arguments a and b), or a horizontal line (argument h), or a vertical line (argument v)

plot(0,0,"n", xlab="", ylab="") 
abline(h=0.5, v=0, col = "purple", lwd = 4)
abline(a=1, b=1, col = "orange", lwd = 4)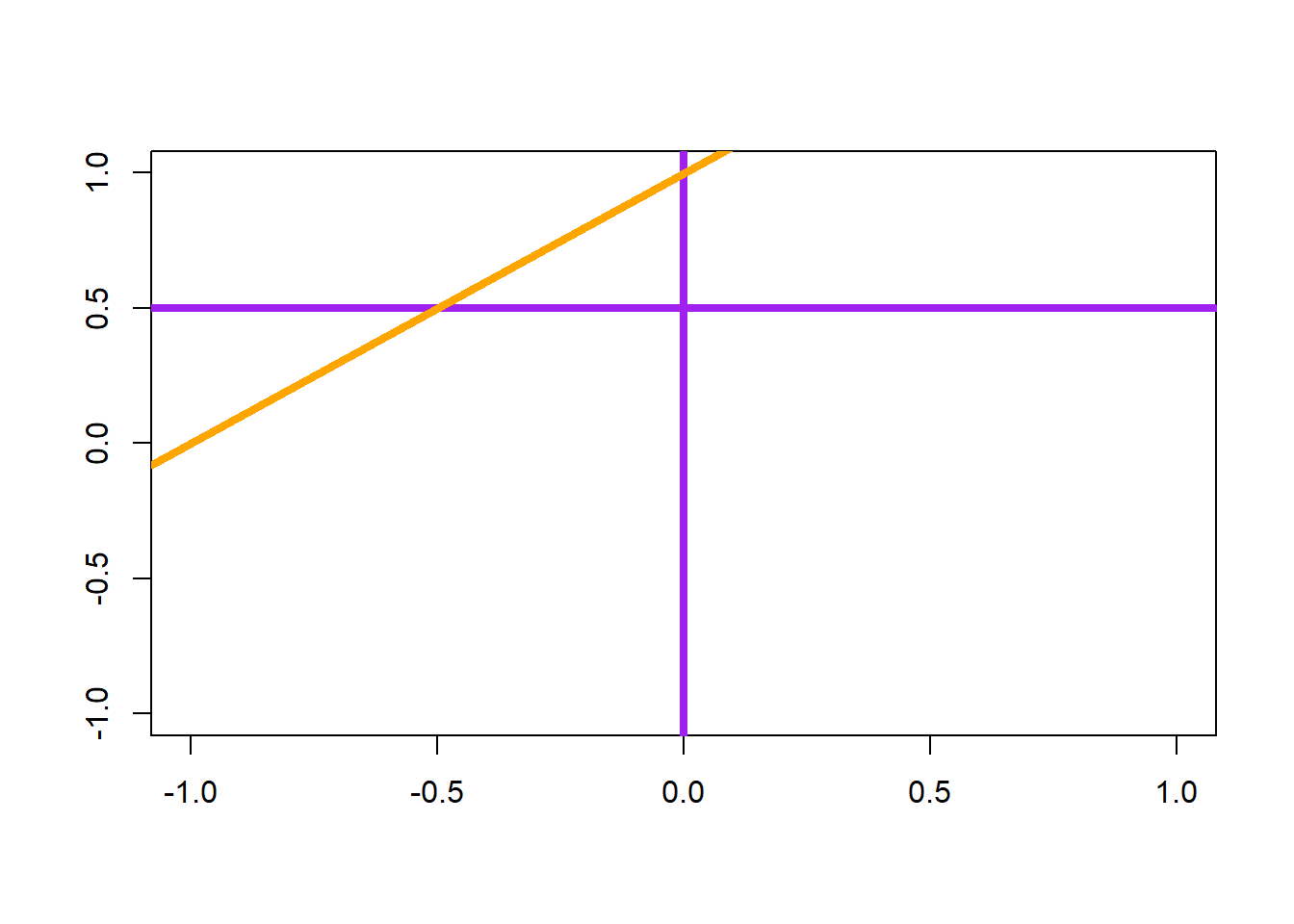

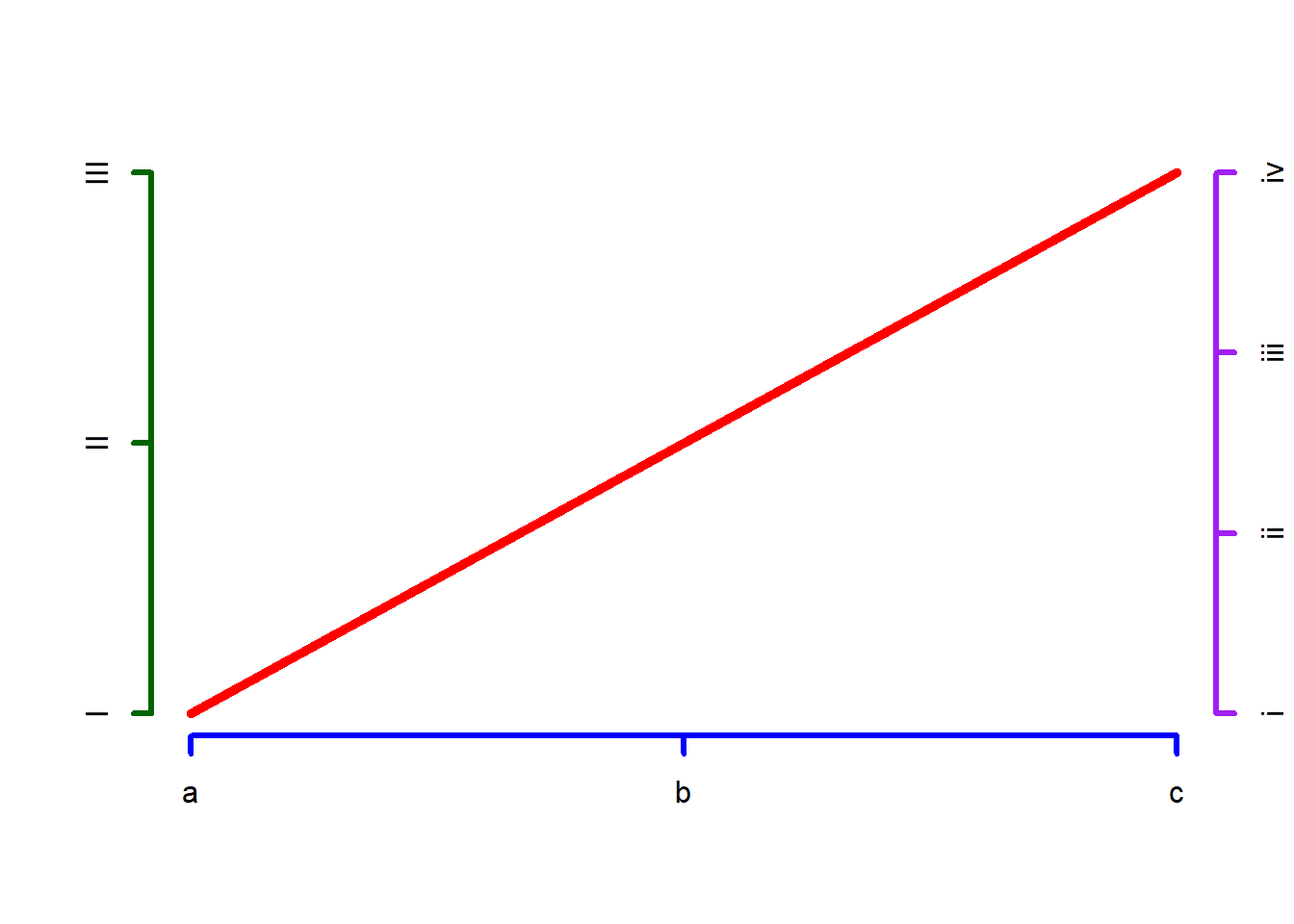
Additional notes: axis - Page 172-173

plot.new()
lines(x=c(0,1), y=c(0,1), col="red", lwd = 5)
axis(side=1, at=c(0, 0.5, 1), labels=c("a","b","c"), col="blue", lwd = 3)
axis(side=2, at=c(0, 0.5, 1), labels=c("I","II","III"), col="darkgreen", lwd = 3)
axis(side=4, at=c(0, 0.333, 0.667, 1), labels=c("i","ii", "iii", "iv"), col="purple", lwd = 3)