Let x=1
Let y=1
Let z=x+y
Repeat (n-3) times the following: # we need (n-3) numbers (since we have the first 3)
re-assign variable x to equal current value of y
re-assign variable y to equal current value of z
re-assign variable z to equal current value of x+y
Return zWeek 7: Algorithms and pseudocode
Learning outcomes
By the end of this topic, you should be able to
- Understand what an algorithm is
- Break down a problem into more manageable tasks
- Understand and apply some fundamental principles for designing algorithms
- Write algorithms as pseudocode
Note: Algorithms are not just for computer science geeks, they are a systematic way to think about and solve almost any problem… and as future actuaries, you are all in the business of problem-solving :-).
What is an algorithm?
Definition
An algorithm is a step by step method of solving a problem, expressed as a finite list of well-defined instructions.
input: an algorithm has zero or more inputs
output: one or more outputs, which are specifically determined by the inputs (if any)
finiteness: must always terminate after a finite number of steps
definiteness: each step must be precisely defined; the actions to be carried out must be rigorously and unambiguously specified
effectiveness: all operations to be performed must be sufficiently basic that they can be done exactly, and in a finite length of time
Algorithms - A simple illustration
Algorithms - Applications
an internet search engine:
input: key words in the search box
output: a sorted list of websites
a trip planner
input: starting position, destination, a map of roads
output: the fastest route
a recommendation system (e.g. YouTube, Netflix, TikTok,…)
input: history of user’s utilisation
output: a suggestion of what they may also like
parameter estimation (in statistics)
input: data, model assumptions
output: estimated parameters (for example by maximising likelihood… more in ACTL2131!)
What is pseudocode?
Definition
‘Pseudocode is a detailed yet readable description of what a computer program or algorithm must do, expressed in a formally-styled natural language rather than in a programming language’.
To be read by humans, not computers.
Must be clear and concise.
Not typically concerned with issues of software engineering.
Example of Algorithm & Pseudocode: The Collatz Sequence
The Collatz sequence goes as follows: start at any positive integer
- if the number is \(1\), stop
- if the number is even, divide it by \(2\)
- if the number is odd, multiply it by \(3\) and add \(1\)
It is conjectured but not proven that the sequence always reaches \(1\), eventually. For example, the Collatz sequence starting at \(5\) is: \[ 5 \to 16 \to 8 \to 4 \to 2 \to 1 \] A function which takes any positive integer and returns the next number in the sequence is an algorithm! Expressed in pseudocode this would look like:
Declare 'collatzNext' as function of x
If x is 1
result is 1
If x is even
result is x/2
Otherwise
result is 3*x + 1
Return resultTo keep exploring:
Advantages of pseudocode
- Allows you to think thoroughly (and plan ahead) before programming something.
- Describes the key steps of an algorithm, but is environment-independent.
- Easier to communicate with others, who possibly don’t know the specific language you are using.
Exercise - Fibonacci sequence
- Starting at \(1,1, \ldots\) every next element of the Fibonacci sequence is obtained by summing the previous two elements: \(1, 1, 2, 3, 5, 8, 13, 21, \ldots\)
- Write pseudocode for an algorithm that finds the \(n^{th}\) term of the Fibonacci sequence.
Sample solution
Pseudocode:
R code:
# We do this in a function with argument n
get_fibo <- function(n){
x <- 1
y <- 1
z <- 2
for (i in 4:n){
x <- y # update x
y <- z # update y
z <- x + y # find next number in sequence
}
return(z)
}
get_fibo(7)[1] 13Beware of infinite loops
As another example of algorithm, consider what we call a ‘happy number’:
- Start with a positive integer
- Replace that number by the sum of the squares of its digits
- Repeat the process until the number EITHER equals \(1\), and in that case you have a happy number :-)
- OR the process loops endlessly in a cycle that does not include \(1\), you then have a sad number :-(
For example, \(19\) is happy:
\[\begin{align*} & 1^2 + 9^2 = 82 \\ & 8^2 + 2^2 = 68 \\ & 6^2 + 8^2 = 100 \\ & 1^2 + 0^2 + 0^2 = 1. \end{align*}\]
\(4\) is sad:
\[\begin{align*} & 4^2 = 16 \\ & 1^2 + 6^2 = 37 \\ & 3^2 + 7^2 = 58 \\ & 5^2 + 8^2 = 89 \\ & 8^2 + 9^2 = 145 \\ & 1^2 + 4^2 + 5^2= 42 \\ & 4^2 + 2^2 = 20 \\ & 2^2 + 0^2 = 4 \\ & 4^2 = 16 \\ & \ldots \end{align*}\]
- Write an algorithm (start with pseudocode) that takes as input a positive integer and returns TRUE if it is happy, FALSE otherwise.
Happy number - Sample Solution
The tricky part here is to realise that if we ever get the same number twice in the sequence, then we don’t have a happy number, and the sequence will repeat itself forever (infinite loop!). If this happens, we then want to exit the process and declare the number sad. So, we need to keep a history of all numbers obtained.
In pseudocode:
# We do the task in a function
Declare function 'is_happy' with argument 'x'
Inside the function:
# We store all numbers of the sequence in a vector, S
Declare a vector S
While x is not 1 AND S contains only unique elements
- Isolate all digits of x: d1, d2, etc.
- Update x as d1^2 + d2^2 + ...
- Add x to vector S
# While loop is now completed
If x = 1, return TRUE
Otherwise, return FALSEIn R code:
is_happy <- function(x){
S <- NULL # declare an empty vector, to contain all numbers of the sequence
# while we have not reached 1, and we have not gotten any duplicates
while (x != 1 && any(duplicated(S)) == F){
x <- as.integer(strsplit(as.character(x), '')[[1]]) # get all digits of x in a vector
x <- sum(x^2)
S <- c(S,x)
}
ifelse(x == 1, "TRUE", "FALSE") # return result
}
is_happy(19)[1] "TRUE"is_happy(4)[1] "FALSE"Example of pseudocode - largest number
Our task is to write an algorithm that finds the largest number in a list of numbers.
While you may know that you could use the max() function in R, we want to think about how we could code such a function ourselves.
To start with, we break it down into smaller tasks. To find the largest number in a list, we have to:
- Check every number in the list
- Keep track of the largest number found so far
This gives us an indication of a list of steps to follow:
- Initialise the largest number as the first number in the list
- Iterate over each number in the list
- Compare each number to the largest number, if it is larger, update the largest number, otherwise, continue iterating
Now constructing the pseudocode is straightforward:
Declare function 'max' with argument 'x'
Inside the function:
Declare variable 'largest' and set it to the first element of x
For each number 'n' in x
If n > largest
Set largest to n
return largestExample of pseudocode - finding the LCM
Our task is to find the lowest common multiple of two numbers, x and y (recall this is the smallest positive integer that is divisible by both x and y).
The naive solution here is to set up a while loop counting from 1 upwards and checking for each number whether it is divisible by both x and y. But this is inefficient.
Perhaps this problem is “simple”, but in general it is not obvious how to make an algorithm more efficient (or even how to solve the problem). Breaking it down can help.
There are two sub-problems here:
- Choosing which numbers to check for the LCM condition.
- Checking whether such numbers are divisible by both x and y.
Breaking the problem down this way allows us to individually consider each component. One possible algorithm to solve this problem is then:
Declare function 'lcm' with arguments 'x' and 'y'
Inside the function:
Declare variable 'largest' and set it to the max of x and y
Declare variable 'smallest' and set it to the min of x and y
For number 'n' starting at largest, incrementing by largest, and ending at x * y:
If n mod smallest is 0:
return n This method exploits the fact that only numbers that are a multiple of the larger number need to be considered. In addition, because we already choose the numbers n such that they are multiples of the larger one, we only need to check whether n is divisible by the smaller one.
Take aways for good pseudocode
Clear structure and steps.
Informative explanations.
Not every detail is there, but each step should be unambiguous. Ask yourself: would a competent programmer be able to implement this without thinking much?
Use indentation: improves readability of codes.
Don’t be afraid to comment (
#comments.R.great) !As an aside, you do not have to exactly follow the syntax used in these slides, the idea is for pseudocode to be a readable set of instructions for any human.
Any fool can write code that a computer can understand. Good programmers write code that humans can understand. ― Martin Fowler
Final remarks on Algorithms
Writing the pseudocode of your algorithm before actually coding is good practice (especially for complex tasks).
Decomposing a problem into several ‘easier’ tasks is, in general, a good approach
Each building block is an doable task
You connect the building blocks to get a solution
Some of these building blocks may be in-built features or functions in
R; knowing exactly what you want the building block to do will help you find an appropriateRfunction
Have efficiency in mind: can the task be done in fewer/faster steps?
The fact modern computers are powerful is not a valid excuse for ‘sloppy’, inefficient programming. In your actuarial careers you will encounter huge datasets, and the running time of your programs is likely to be relevant. Be efficient!
Sadly, learning to think about problems algorithmically is not something we can completely teach via slides, so you are strongly encouraged to practice with as many of the homework exercises as you can.
More Advanced Algorithm Concepts
This content is not assessable, but is worthwhile if you are interested.
If not, skip to the homework tasks at the end.
Divide and Conquer Method
The ‘Divide and Conquer’ method to design an algorithm breaks down a complex task into simpler blocks, or ‘sub-problems’ that share the same structure as the main problem, but are easier to deal with.
We can then write an algorithm to solve the sub-problems, and use those solutions to solve the main problem. Those algorithms have the general structure:
- Divide: Break the given problem into (smaller/simpler) sub-problems of the same type.
- Conquer: Recursively solve these sub-problems.
- Combine: Appropriately combine the answers to get the solution of the original problem.
Divide and Conquer: An Exercise
You are given a sorted list of numbers: \(A = (n_1, n_2, \ldots)\) and another number, say \(N\), which might be in the list. You want to find if the number is in the list and if so, its position in the list.
How would you apply the divide and conquer method to solve this? Write this as pseudocode.
Possible Solution
A ‘naive’ solution would be to scan all the numbers, and stop whenever you find \(N\). That would work, but would not be efficient.
Instead, we can take advantage of the fact the list is sorted. General strategy:
- Look at the middle number, if it is equal to \(N\), you are done.
- Keep only half the numbers where \(N\) can possibly be: the first half if \(N <\) middle, the second half if \(N >\) middle. Find the middle of that half and start again.
- When the process is done, return the position of the number if you found it, or return ‘unsuccessful’ otherwise
In pseudocode:
# Let the list be A, with A[i] its i^th element
# Set the Left (L) and Right (R) indices of your searching range
L = 1 and R = n
If N < A[L] OR N > A[R], return 'unsuccessful'
Let m = floor((L+R)/2) # Update the middle point
If (A[m] == N), return m (the search is done)
If R = L, return 'unsuccessful'
If A[m]<N, let L = m + 1 and go back to step "let m = floor(..)"
If A[m]>N, let R = m - 1 and go back to step "let m = floor(..)"In R code:
# We put this in a function 'find_N'
find_N <- function(A, N){
L <- 1 # Set left bound at 1st position
R <- length(A) # Set right bound at last position
if (N < A[L] || N > A[R]){return('unsuccessful')}
found <- F # Thus far, N has not be found
while (found == F){ # As long as we have not found N, we will keep going
m <- floor((L+R)/2) # Update the middle point
if (A[m] == N){return(paste(N, "is in position",m))}
if (R == L){return('unsuccessful')}
if (A[m]<N){L <- m + 1} # if N is bigger than middle point, update left bound
if (A[m]>N){R <- m - 1} # if N is smaller than middle point, update right bound
}
} # End function
find_N(A=1:50, N = 42)[1] "42 is in position 42"find_N(A=c(4,8,10,12,14), N = 12)[1] "12 is in position 4"find_N(A=c(4,8,10,12,14), N = 13) [1] "unsuccessful"More on Algorithms: Recursion
Recursion is a popular approach in ‘dividing and conquering’ a problem.
To cite this Reference:
‘The process in which a function calls itself directly or indirectly is called recursion and the corresponding function is called as recursive function. Using recursive algorithm, certain problems can be solved quite easily.’
- Each step in the recursion gets you closer to the solution, by solving a smaller/simpler (but identical) version of the original problem.
An old joke: To understand recursion you must first understand recursion.
Three Laws of Recursion
A recursive algorithm needs to follow three important ‘Laws’:
- A recursive algorithm must have a base case. When such a base case is reached, the algorithm terminates.
- At each new step, a recursive algorithm must change its state and progress towards the base case.
- A recursive algorithm must call itself, recursively.
Example
This is best understood through a simple example. Suppose we want to compute \(n! = n \times (n-1) \times \dots \times 1\). A classical way to do this is to use a loop as follows:
n <- 10
result<-1
for (i in 1:n){
result<-result*i
}
result[1] 3628800A recursive solution would require us to define a function my.factorial(n) which is used inside itself!
my.factorial<-function(n){
# This is the base case
if (n==1){
return(1)
}
# If we are not at the base case, the algorithm moves towards the base case by calling itself
else{
return(n*my.factorial(n-1))
}
}
my.factorial(10)[1] 3628800Breakdown
The \(\verb|my.factorial(10)|\) function call does the following:
\(10 \times \verb|my.factorial(9)|\)
\(10 \times 9 \times \verb|my.factorial(8)|\)
\(10 \times 9 \times 8 \times \verb|my.factorial(7)|\)
\(\dots\)
\(10 \times 9 \times 8 \times \dots 2 \times \verb|my.factorial(1)|\)
\(\verb|my.factorial(1)|\) returns \(1\) because we defined this behaviour here: [ ]
Necessary properties of recursion
- Handles a simple base case, whose solution is obvious
- Each call of the function gets you closer to the solution
- Avoids infinite cycles, i.e., you know it will eventually terminate!
Exercise
Write a recursive algorithm that returns the \(n^{\text{th}}\) number in the Fibonacci sequence \(1,1,2,3,5,8,13,\ldots\)
Solution
my.fibo <-function(n){
# This is the base case
if (n==1 || n==2){
return(1)
}
# If we are not at the base case, the algorithm moves towards the base case by calling itself
else{
return(my.fibo(n-1) + my.fibo(n-2))
}
}
my.fibo(7)[1] 13Note: This is a simple example to illustrate what a recursive algorithm is. However, it is a rather inefficient may of solving the Fibonacci sequence problem (much slower than a previous solution we gave). Can you see why?
Advanced Algorithm: PageRank
Algorithms are the building blocks of computer programs. A historically very important algorithm (and still used today) is PageRank, the ranking system invented by Google co-founders Larry Page and Sergey Brin.
PageRank gives a score to any webpage (in a given network). This score represents the probability that a person who is randomly clicking links on the Internet lands on that specific page.
So if a page \(A\) has a \(0.5\) PageRank within a network, and someone is randomly clicking on links, there is a \(50\%\) chance this person will be directed to page \(A\) after clicking randomly on a given link.
The overall idea behind PageRank is very simple: pages that receive more links from other pages should have a higher score, see the illustration below. Each smiley face represents a webpage, and each pointed finger represents an outbound link from one page to another. The size of each smiley face is proportional to their Page Rank.
Said otherwise: PageRank gives a page’s ‘popularity’; websites that are frequently linked to have higher PageRanks.

The license for the image above can be found here.
PageRank (Continued)
More formally, call \(A\) some webpage, then
\[PR(A) = \frac{1-d}{N} + d \left(\frac{PR(T_1)}{C(T_1)} + ... + \frac{PR(T_n)}{C(T_n)}\right)\] Where:
-\(PR(A)\) is the PageRank of page \(A\)
-\(N\) is the total number of pages in the network
-\(PR(T_i)\) is the PageRank of pages \(T_i\) which links to page \(A\)
-\(C(T_i)\) is the total number of outbound links from page \(T_i\) to other pages
-\(d\) is a damping factor which can be set between \(0\) and \(1\) (we take it as \(1\) for the remainder of this section, and leave it to you to investigate it further if you are interested)
PageRank (Continued)
PageRanks are calculated recursively because the PageRank of a webpage \(A\) depends on the PageRank of other webpages, which in turn are dependent on the PageRank of \(A\)…
Larry Page and Sergey Brin showed in their research paper that the PageRanks will eventually converge (why this is the case is outside the scope of this course), meaning that the algorithm will eventually terminate. Back then (1998), it took 52 iterations for the PageRanks of 322 million webpages to be determined.
PageRank example
Assume that \(d=1\) and that there are only \(N=4\) websites on the internet: \(A\), \(B\), \(C\) and \(D\). Links are given by the image below. That is, \(A\) has a link to \(C\) only. \(B\) has a link to \(A\) and \(D\). \(C\) has a link to all three other pages. \(D\) has a link to \(A\) only.
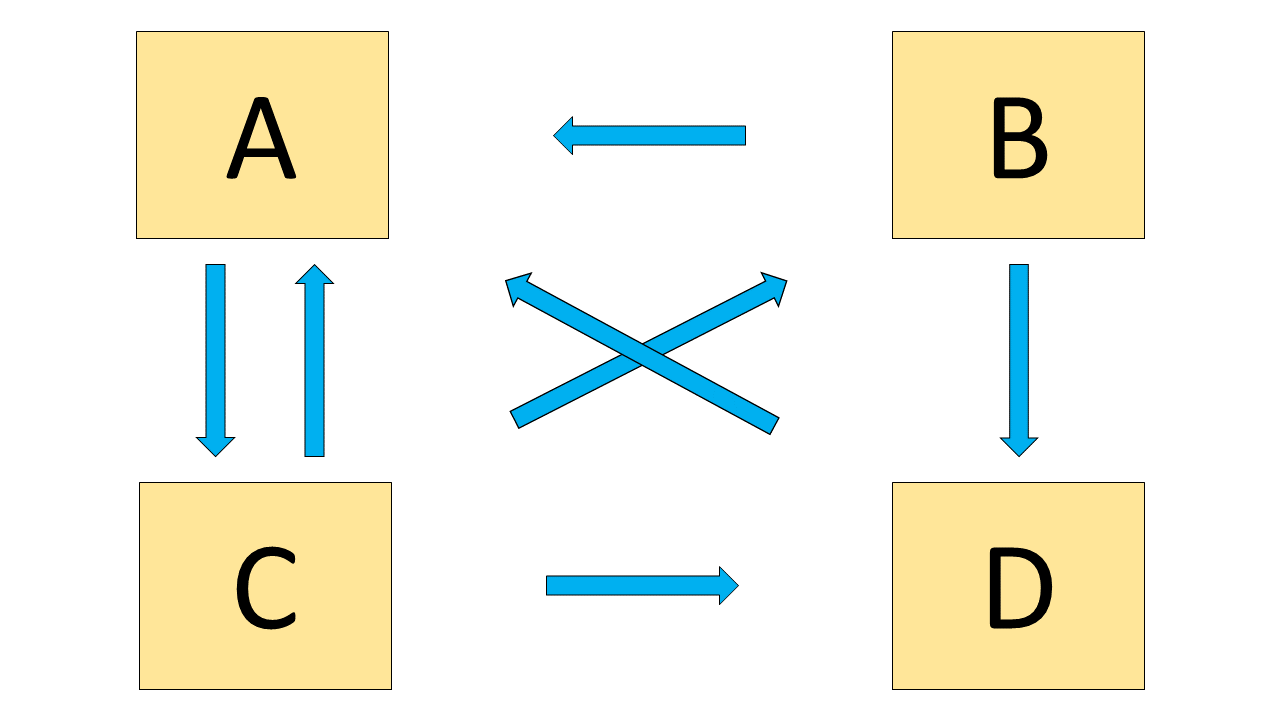
- Initially, all Pages are assigned the same rank, \(1/4 = 0.25\).
- At the first iteration, we have \[\begin{align*} PR(A) & = \frac{0.25}{2} + \frac{0.25}{3} + \frac{0.25}{1} = 11/24 \\ PR(B) & = \frac{0.25}{3} = 2/24 \\ PR(C) & = \frac{0.25}{1} = 6/24 \\ PR(D) & = \frac{0.25}{2} + \frac{0.25}{3} = 5/24 \\ \end{align*}\]
- Then for the second iterations, we use the new Page Ranks obtained in the first one to get updated Pages Ranks, i.e. \[\begin{align*} PR(A) & = \frac{2/24}{2} + \frac{6/24}{3} + \frac{5/24}{1} = 8/24 \\ PR(B) & = \frac{6/24}{3} = 2/24 \\ PR(C) & = \frac{11/24}{1} = 11/24 \\ PR(D) & = \frac{2/24}{2} + \frac{6/24}{3} = 3/24 \\ \end{align*}\]
- And so on… Can you write an
Rprogram to do this automatically and find the converging \(PR\) values?
Homework Exercises
Homework Exercises - General Instructions
While several of these tasks can be solved using features or functions of
R, you are encouraged to think of how you would solve the problem in more elementary steps.If there is a problem that you could solve using vectorisation or some in-built function, try to imagine how the function works internally and use that as your pseudocode.
It is good to be aware of how to solve things the
Rway, but not all problems can be solved this way, so it is important to understand the underlying logic of algorithms.
Homework Exercise 1
Describe how the following tasks can be broken down into smaller tasks:
Given their raw marks (from 0 to 100), classify a group of students using the UNSW grading system (HD, D,…)
Given a sentence, reverse the letters of each word individually, i.e. ‘Hello World’ becomes ‘olleH dlroW’. You do not have to specify the exact steps, just what each subtask would require.
If you have done these, feel free to try and write more precise pseudocode, and then implement them in R.
Homework Exercise 2
In pseudocode, describe how you might (there will be many solutions):
Find the number of students who passed given a list of student’s marks
Detect whether a given word is a palindrome (i.e. it reads the same backwards and forwards, like ‘radar’ or ‘level’). You can assume the word is provided as a vector of characters rather than a string, e.g.
c('r','a','d','a','r').
Homework Exercise 3
Write an algorithm that determines the sum of all numbers less than 100 that are multiples of 3 or 5.
Homework Exercise 4
The so called ‘golden ratio’ is an important number in mathematics. It has value \(\varphi = (1+ \sqrt{5})/2 \approx 1.618034\). It is an irrational number, but there is an identity saying it is also equal to the ‘infinite fraction’:
\[ \varphi = 1 + \frac{1}{1+ \frac{1}{1 + \frac{1}{1 +\ldots}}}\] While this fraction never ends, we can ‘chop it’ at any point to get an approximation of \(\varphi\). The further we go, the better the approximation. For instance: \[ \varphi \approx 1 + \frac{1}{1+ \frac{1}{1 + 1}} = 5/3 = 1.\bar{6}\] Which can be improved by: \[ \varphi \approx 1 + \frac{1}{1+ \frac{1}{1 + \frac{1}{1 + 1}}} = 8/5 = 1.6\] Which can be improved by \[ \varphi \approx 1 + \frac{1}{1+ \frac{1}{1 + \frac{1}{1 + \frac{1}{1+1}}}} = 13/8 = 1.625\] Write an algorithm that computes this approximation, until further improvement is smaller than a fixed threshold (e.g. 0.0001).
Homework Exercise 5
A similar identity exists to express the number \(e\) as an infinite fraction:
\[ e = 2 + \frac{1}{1+ \frac{1}{2 + \frac{2}{3 + \frac{3}{4+ \frac{4}{5 + \ldots}}}}} \] Beautiful, is it not? Write an algorithm that uses this identity to find an approximation of \(e\), until further improvement is smaller than a fixed threshold (e.g. 0.0001).
Homework Exercise 6
Write an algorithm to find the number of prime numbers less than 100,000.
Homework Exercise 7
Write an algorithm that finds the largest prime factor of a given number.
For example the prime factors of 13195 are 5, 7, 13 and 29, so your algorithm should return 29.
Bonus task (hard): as the numbers get larger, you have to make your algorithm much more efficient. Try and rework the algorithm so that you can find the largest prime factor of \(600851475143\). You should get a result of 6857.
Homework Exercise 8 (Warning: hard problem)
Write an algorithm that sorts a list of numbers from smallest to largest.
Hint: google insertion sort if you have no idea where to start. There’s a visualisation of it below
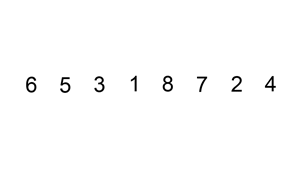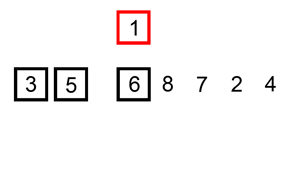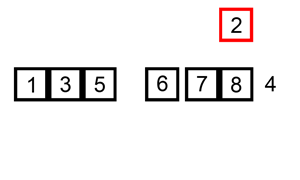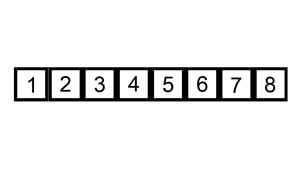
Homework Exercise 9 (Warning: hard problem)
Packing a bag, with duplicate items allowed
You have \(n\) types of items; all items of kind \(i\) are identical and of weight \(w_i\) and value \(v_i\). You also have a backpack of capacity \(C\). Choose a combination of available items which all fit in the backpack and whose value is as large as possible. You can take any number of items of each kind.
Homework Exercise 10 (Warning: very hard problem)
There are \(N\) lily pads in a row. A frog starts on the leftmost lily pad and wishes to get to the rightmost one. The frog can only jump to the right. There are two kinds of jump the frog can make:
- The frog can jump \(3\) lily pads to the right (skipping over two of them)
- The frog can jump \(5\) lily pads to the right (skipping over four of them)
Each lily pad has some number of flies on it. Design an algorithm that maximises the total number of flies the frog lands on while getting to the rightmost lily pad.
The input of the algorithm is a vector containing the number of fies on each lily pad, from left to right, e.g.
c(1,1,1,20,1,1,1,1,1,1,1,1,1,1,1,1)The output should be the total number of flies the frog landed on.
You can assume the input vector is valid, i.e. that it is possible for the frog to reach the right side by jumps of 3 and 5.
Example: if the Input is lilypads <- c(1,1,1,20,1,1,1,1,1,1,1,1,1,1,1,1), then it advantageous to do jumps of 3, and the output should be 25. But if say lilypads <- c(1,1,1,1,1,20,1,1,1,1,1,1,1,1,1,1), then it is advantageous to do jumps of 5, and the output should be 23.
Hint: a popular algorithmic paradigm for solving this is dynamic programming.