Lab 8: Tree-based Methods

Questions

Conceptual Questions

  1. \star Solution (ISLR2, Q8.3) Consider the Gini index, classification error, and entropy in a simple classification setting with two classes. Create a single plot that displays each of these quantities as a function of \hat{p}_{m1}. The x-axis should display \hat{p}_{m1}, ranging from 0 to 1, and the y-axis should display the value of the Gini index, classification error, and entropy.

    Hint: In a setting with two classes, \hat{p}_{m1} = 1 - \hat{p}_{m2}. You could make this plot by hand, but it will be much easier to make in R.

  2. \star Solution (ISLR2, Q8.4) This question relates to the plots in the textbook Figure 8.14, reproduced here as Figure 1:

    Figure 1: Left: A partition of the predictor space corresponding to Exercise 4a. Right: A tree corresponding to Exercise 4b.

    1. Sketch the tree corresponding to the partition of the predictor space illustrated in the left-hand panel of Figure 8.14. The numbers inside the boxes indicate the mean of Y within each region.

    2. Create a diagram similar to the left-hand panel of Figure 8.14, using the tree illustrated in the right-hand panel of the same figure. You should divide up the predictor space into the correct regions, and indicate the mean for each region.

  3. \star Solution (ISLR2, Q8.5) Suppose we produce ten bootstrapped samples from a data set containing red and green classes. We then apply a classification tree to each bootstrapped sample and, for a specific value of X, produce 10 estimates of \mathbb{P}(\text{Class is Red}|X): 0.1, 0.15, 0.2, 0.2, 0.55, 0.6, 0.6, 0.65, 0.7, \text{ and } 0.75. There are two common ways to combine these results together into a single class prediction. One is the majority vote approach discussed in this chapter. The second approach is to classify based on the average probability. In this example, what is the final classification under each of these two approaches?

Applied Questions

  1. \star Solution (ISLR2, Q8.8) In the lab, a classification tree was applied to the Carseats data set after converting Sales into a qualitative response variable. Now we will seek to predict Sales using regression trees and related approaches, treating the response as a quantitative variable.

    1. Split the data set into a training set and a test set.

    2. Fit a regression tree to the training set. Plot the tree, and interpret the results. What test MSE do you obtain?

    3. Use cross-validation in order to determine the optimal level of tree complexity. Does pruning the tree improve the test MSE?

    4. Use the bagging approach in order to analyze this data. What test MSE do you obtain? Use the importance() function to determine which variables are most important.

    5. Use random forests to analyze this data. What test MSE do you obtain? Use the importance() function to determine which variables are most important. Describe the effect of m, the number of variables considered at each split, on the error rate obtained.

    6. Optional: Now analyze the data using BART, and report your results.

  2. Solution(ISLR2, Q8.9) This problem involves the OJ data set which is part of the ISLR2 package.

    1. Create a training set containing a random sample of 800 observations, and a test set containing the remaining observations.

    2. Fit a tree to the training data, with Purchase as the response and the other variables as predictors. Use the summary() function to produce summary statistics about the tree, and describe the results obtained. What is the training error rate? How many terminal nodes does the tree have?

    3. Type in the name of the tree object in order to get a detailed text output. Pick one of the terminal nodes, and interpret the information displayed.

    4. Create a plot of the tree, and interpret the results.

    5. Predict the response on the test data, and produce a confusion matrix comparing the test labels to the predicted test labels. What is the test error rate?

    6. Apply the cv.tree() function to the training set in order to determine the optimal tree size.

    7. Produce a plot with tree size on the x-axis and cross-validated classification error rate on the y-axis.

    8. Which tree size corresponds to the lowest cross-validated classification error rate?

    9. Produce a pruned tree corresponding to the optimal tree size obtained using cross-validation. If cross-validation does not lead to selection of a pruned tree, then create a pruned tree with five terminal nodes.

    10. Compare the training error rates between the pruned and unpruned trees. Which is higher?

    11. Compare the test error rates between the pruned and unpruned trees. Which is higher?

    Solution

  3. \star Solution(ISLR2, Q8.10) We now use boosting to predict Salary in the Hitters data set.

    1. Remove the observations for whom the salary information is unknown, and then log-transform the salaries.

    2. Create a training set consisting of the first 200 observations, and a test set consisting of the remaining observations.

    3. Perform boosting on the training set with 1,000 trees for a range of values of the shrinkage parameter \lambda. Produce a plot with different shrinkage values on the x-axis and the corresponding training set MSE on the y-axis.

    4. Produce a plot with different shrinkage values on the x-axis and the corresponding test set MSE on the y-axis.

    5. Compare the test MSE of boosting to the test MSE that results from applying two of the regression approaches seen in Chapters 3 and 6.

    6. Which variables appear to be the most important predictors in the boosted model?

    7. Now apply bagging to the training set. What is the test set MSE for this approach?

Solutions

Conceptual Questions

  1. Question See Figure 2.

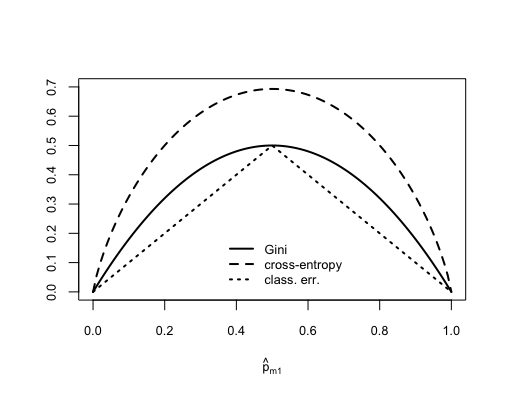
    Figure 2: The Gini index, classification error, and cross-entropy in a simple classification setting with two classes.

  2. Question

    1. See Figure 3.

      Figure 3: The tree corresponding to the partition of the predictor space illustrated in the left-hand panel of Figure 8.12.

    2. See Figure 4.

      Figure 4: The partition of the predictor space corresponding to the right-hand panel of Figure 8.12.

  3. Question Majority approach: the number of red predictions is greater than the number of green predictions based on a 50% threshold, thus our prediction is RED.
    Average approach: the average of the probabilities is less than the 50% threshold, thus our prediction is GREEN.

Applied Questions

  1. Question

    1. library(ISLR2)
set.seed(1)
train.set <- sample(nrow(Carseats), nrow(Carseats) / 2)
train <- 1:nrow(Carseats) %in% train.set
    2. library(tree)
fit <- tree(Sales ~ ., data = Carseats, subset = train)
plot(fit)
text(fit, pretty = 0)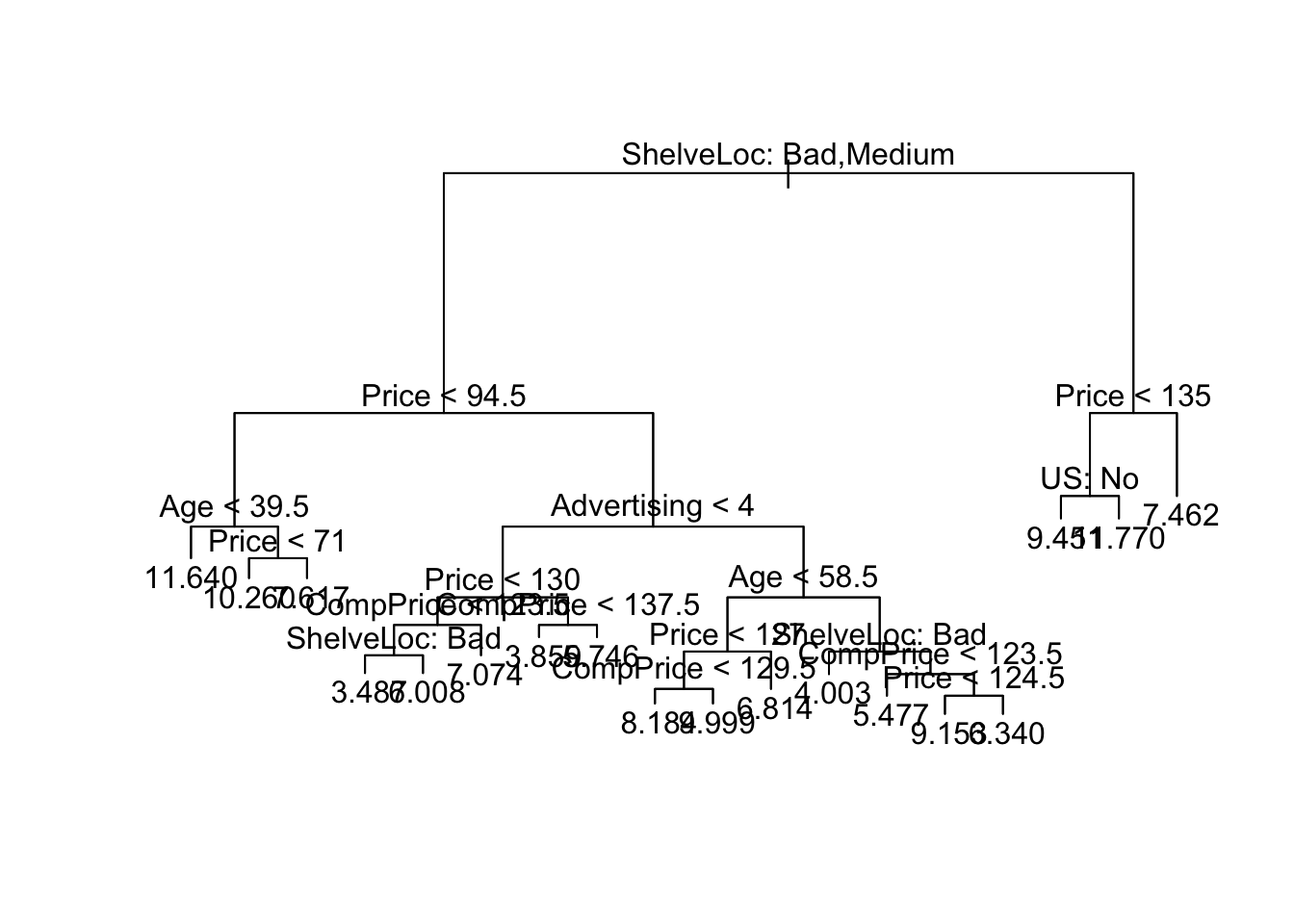

      pred <- predict(fit, newdata = Carseats[!train, ])
(test.mse <- mean((Carseats$Sales[!train] - pred)^2))
      [1] 4.922039

      The test MSE is about 4.92. Unfortunately, the plot doesn’t look too nice. Let’s try our luck with fitting function rpart() from library rpart and plotting function rpart.plot() from library rpart.plot (lots of libraries, I know).

      library(rpart)
library(rpart.plot)
fit.rpart <- rpart(Sales ~ ., data = Carseats, subset = train)
rpart.plot(fit.rpart)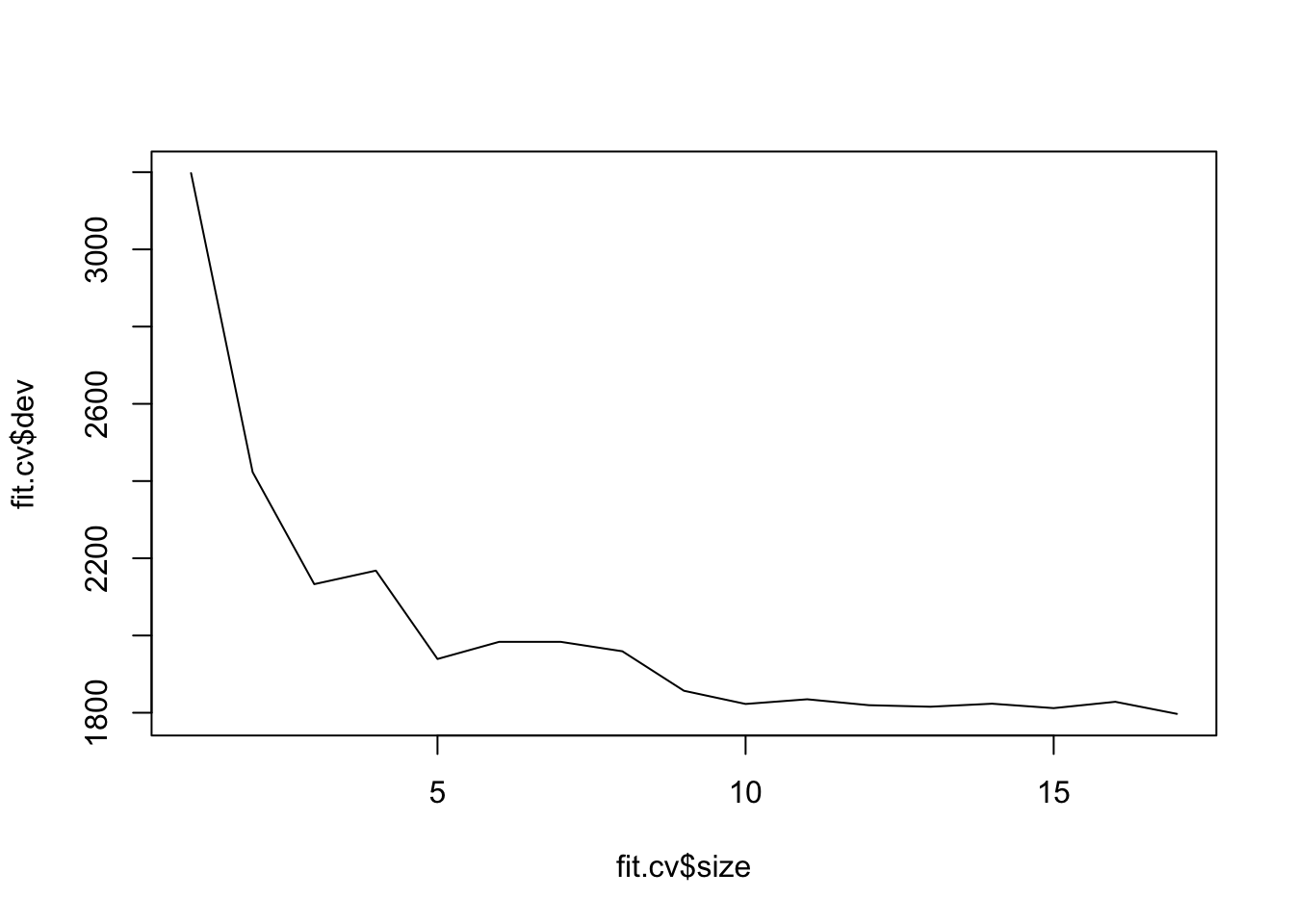

      Much better! We see that ShelveLoc seems to be the most important predictor of sales (split at the top level), then price.

    3. set.seed(123)
fit <- tree(Sales ~ ., data = Carseats)
fit.cv <- cv.tree(fit, FUN = prune.tree)
fit.cv
      $size
 [1] 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2  1

$dev
 [1] 1967.759 1974.584 1988.813 2000.033 1972.183 1951.005 1961.298 1956.632
 [9] 1928.169 1935.336 1915.630 1910.497 1876.414 2079.084 2122.798 2411.275
[17] 3199.248

$k
 [1]      -Inf  32.78204  33.43341  34.30000  37.83019  38.65535  40.44960
 [8]  41.83218  51.05171  70.52963  76.20847  76.57441 106.90014 145.33849
[15] 162.67977 334.36974 797.19286

$method
[1] "deviance"

attr(,"class")
[1] "prune"         "tree.sequence"
      plot(fit.cv$size, fit.cv$dev, type = "l")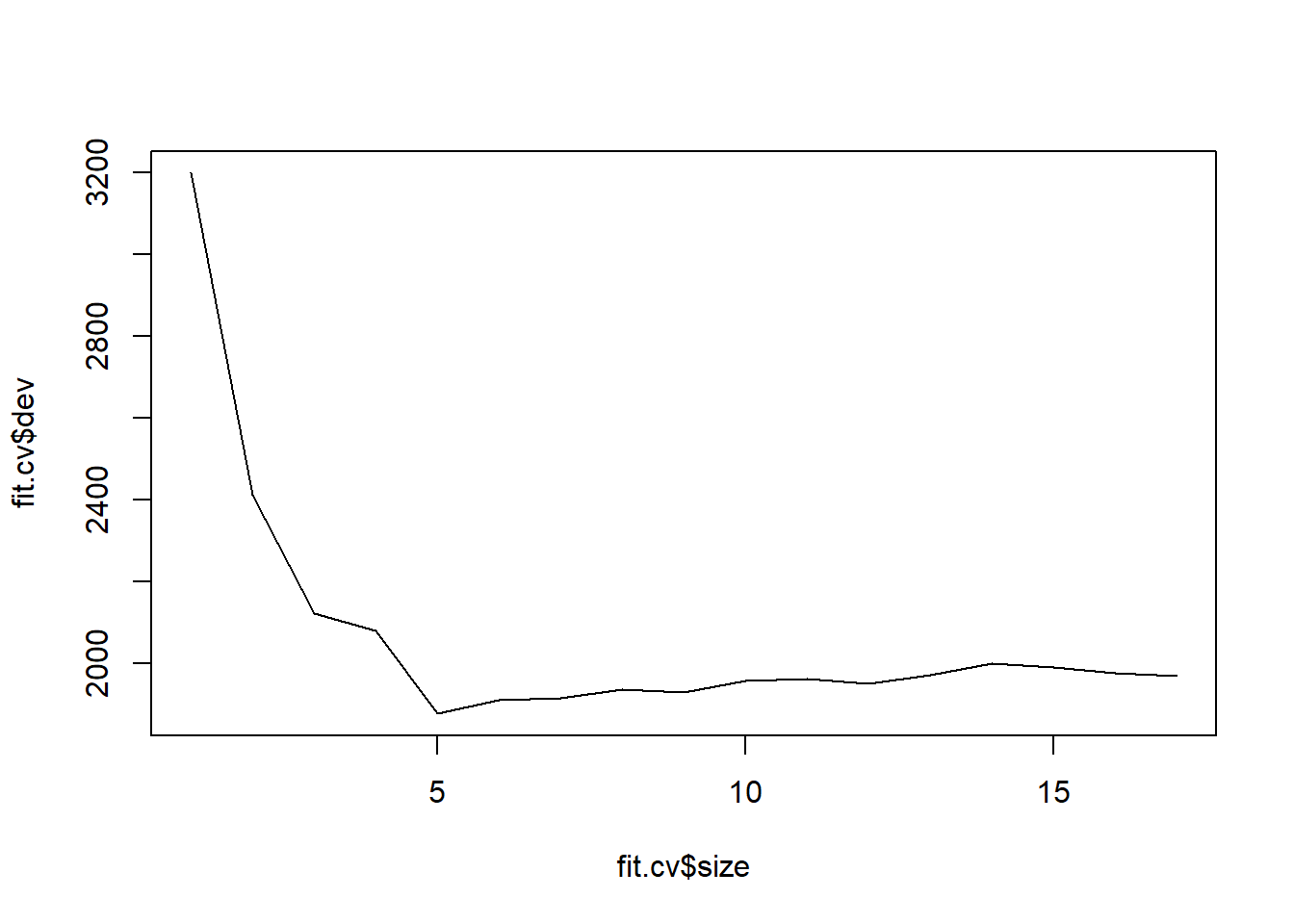

      (index.min <- which.min(fit.cv$dev))
      [1] 13
      (size.min  <- fit.cv$size[index.min])
      [1] 5
      plot(fit.cv$k, fit.cv$dev, type = "l")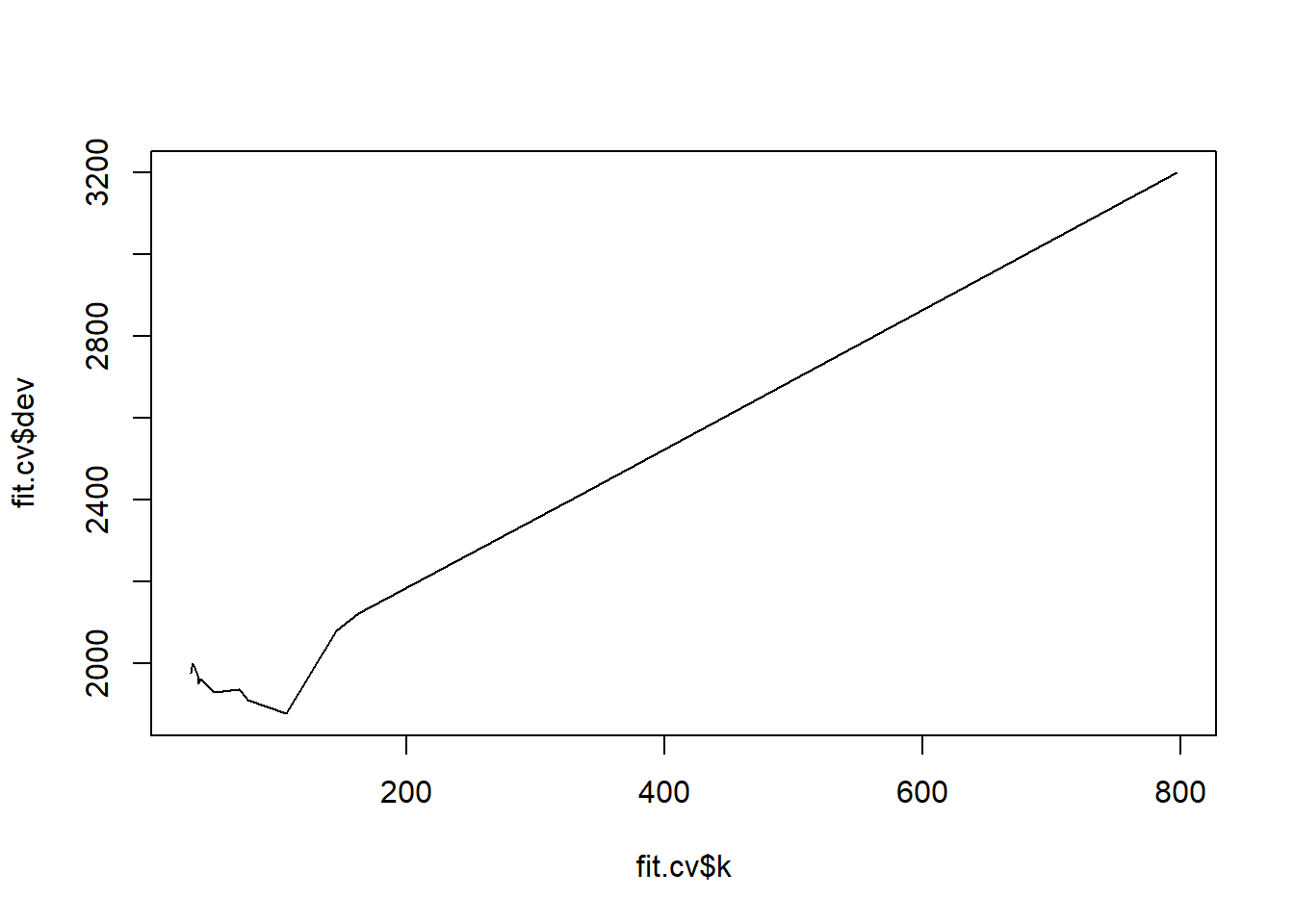

      The model with the lowest CV error is the tree with 5 leaves. It has a cost-complexity tuning parameter of 106.9. Note the package calls the error “dev” for “deviance”, but this is equivalent to using the MSE.

    4. library(randomForest)
      randomForest 4.7-1.2
      Type rfNews() to see new features/changes/bug fixes.
      set.seed(123)
bag.sales <- randomForest(Sales ~ .,
  data = Carseats, subset = train,
  mtry = (ncol(Carseats) - 1), importance = TRUE
)
pred <- predict(bag.sales, newdata = Carseats[!train, ])
(test.mse <- mean((Carseats$Sales[!train] - pred)^2))
      [1] 2.652066
      importance(bag.sales)
                      %IncMSE IncNodePurity
CompPrice   27.42854862    170.440734
Income       6.56405959     91.312337
Advertising 12.85200538    100.645018
Population  -2.04530513     59.661563
Price       58.76321243    504.436464
ShelveLoc   46.41245711    364.580688
Age         15.71122036    156.907404
Education   -0.48769025     42.691633
Urban        0.08928404      9.762364
US           4.29506266     17.020419

      The test error rate is 2.65, which is lower than the non-bagged regression tree model. Price and ShelveLoc are the most important predictors.

    5. set.seed(123)
rf.sales <- randomForest(Sales ~ .,
  data = Carseats, subset = train,
  importance = TRUE
)
pred <- predict(rf.sales, newdata = Carseats[!train, ])
(test.mse <- mean((Carseats$Sales[!train] - pred)^2))
      [1] 3.025767
      importance(rf.sales)
                    %IncMSE IncNodePurity
CompPrice   13.865262     154.23523
Income       1.690171     125.21748
Advertising  8.323675     111.76694
Population  -3.143677     100.12141
Price       37.650327     387.58115
ShelveLoc   34.985856     294.92334
Age         12.057578     171.39258
Education   -1.886551      75.67822
Urban        0.478542      16.63811
US           4.326428      31.86351

      The test error rate is 3.03, which is lower than with the nonbagged regression tree model, but higher than the bagged regression tree model. Price and ShelveLoc predictors are most important, but their effect is understated compared to bagging.

      set.seed(1)
rfTestMSE <- rep(Inf, ncol(Carseats) - 1)
for (i in 1:(ncol(Carseats) - 1)) {
  rf.sales <- randomForest(Sales ~ .,
    data = Carseats, subset = train, mtry = i,
    importance = TRUE
  )
  pred <- predict(rf.sales, newdata = Carseats[!train, ])
  rfTestMSE[i] <- mean((Carseats$Sales[!train] - pred)^2)
}
plot(1:(ncol(Carseats) - 1), rfTestMSE, type = "l")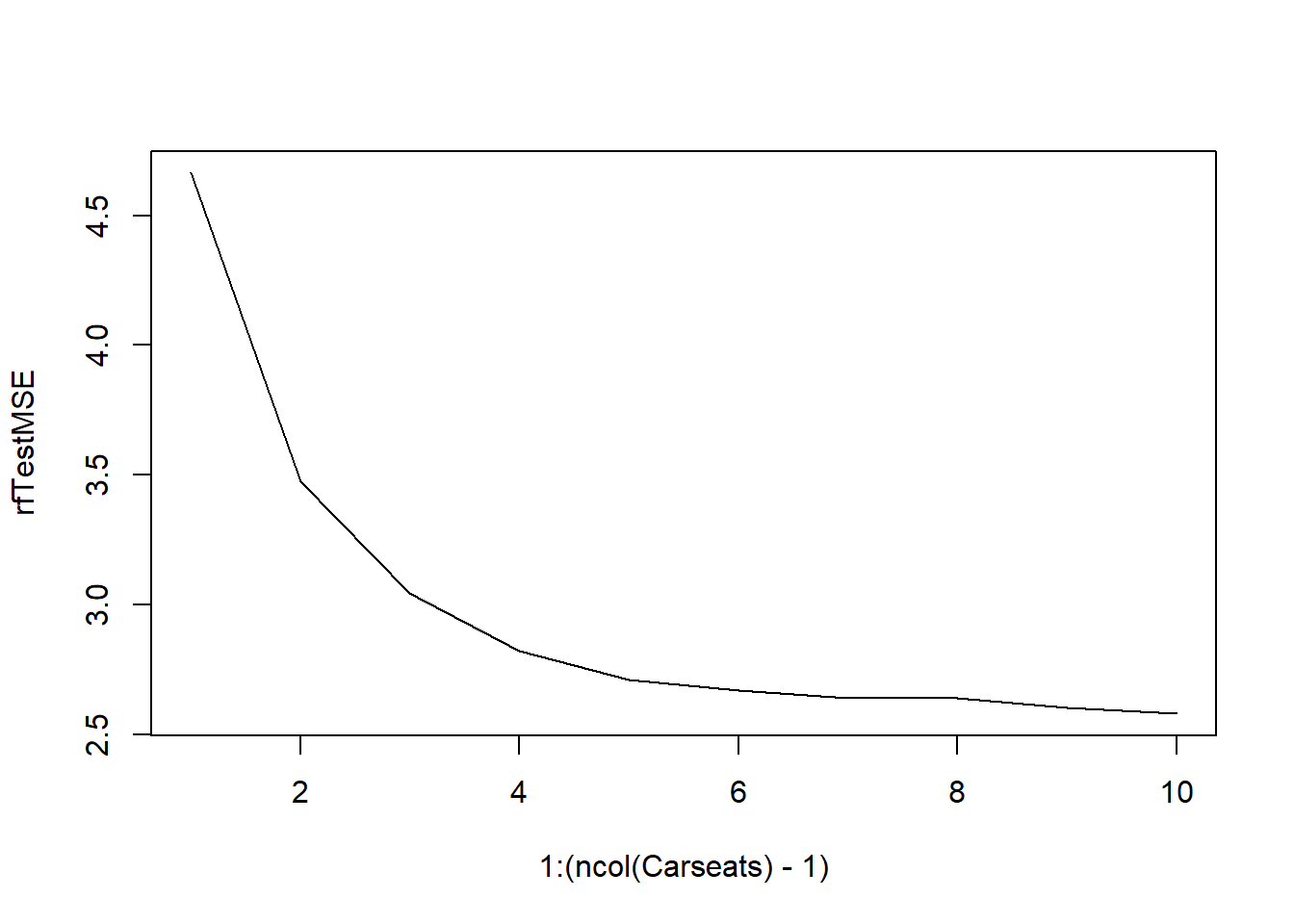

      As expected, the test MSE shows a decreasing trend as the number of variables included in each random forest increases.

  2. Question

    1. library(ISLR2)
set.seed(1)
train.set <- sample(1:nrow(OJ), 800)
train <- 1:nrow(OJ) %in% train.set
    2. library(tree)
OJ.tree <- tree(Purchase ~ ., data = OJ, subset = train)
summary(OJ.tree)
      
Classification tree:
tree(formula = Purchase ~ ., data = OJ, subset = train)
Variables actually used in tree construction:
[1] "LoyalCH"       "PriceDiff"     "SpecialCH"     "ListPriceDiff"
[5] "PctDiscMM"    
Number of terminal nodes:  9 
Residual mean deviance:  0.7432 = 587.8 / 791 
Misclassification error rate: 0.1588 = 127 / 800

      The training error rate is 0.165 with 8 terminal nodes.

    3. # you can type in the tree name "OJ.tree"
# here but it is easier to see in plot form
plot(OJ.tree)
text(OJ.tree)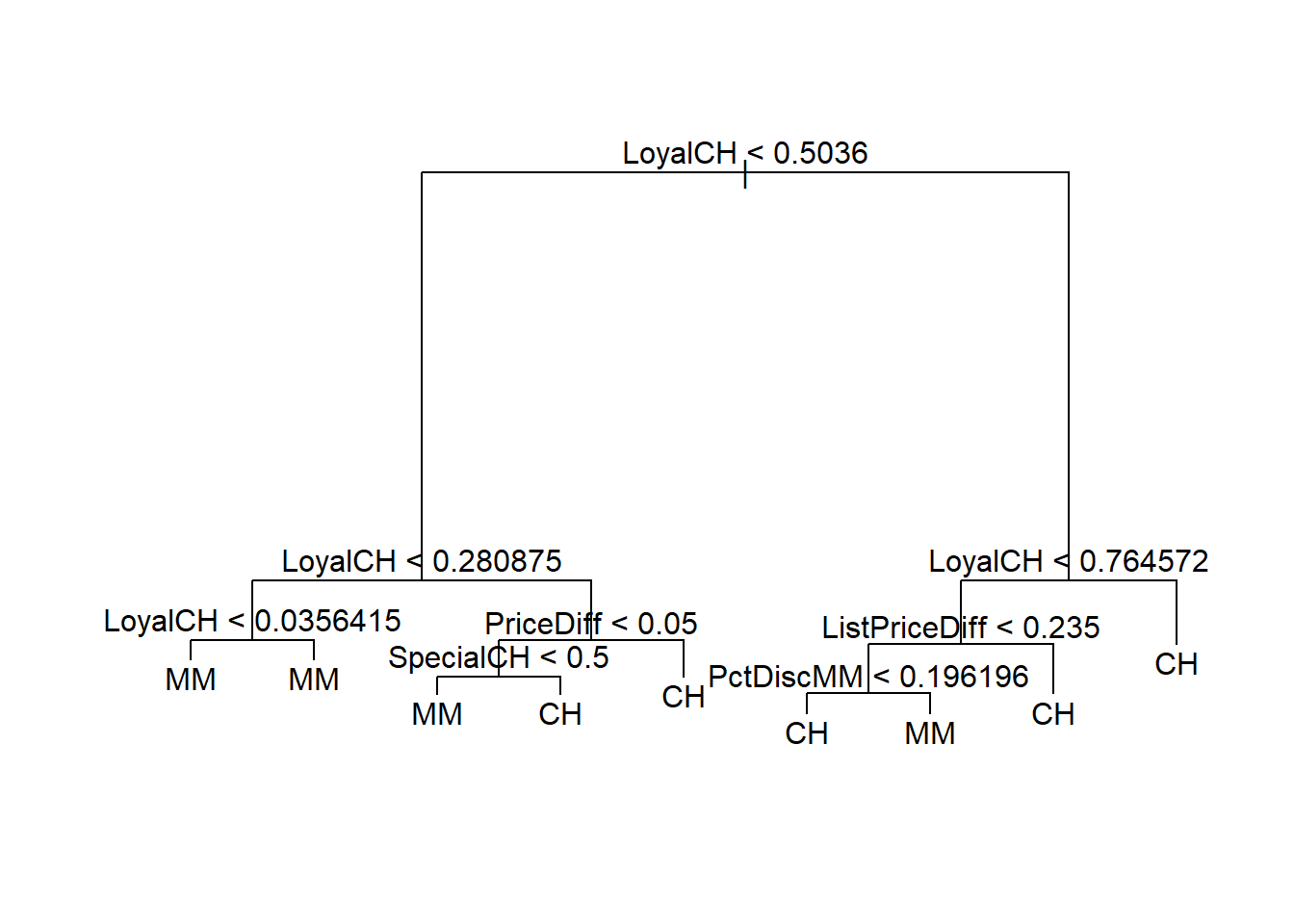

      Consider the 4th leaf-node from the left: if 0.2809 < LoyalCH < 0.5036 and PriceDiff < 0.05 and SpecialCH > 0.5, then classify as CH.

    4. See (c).

    5. pred <- predict(OJ.tree, newdata = OJ[!train, ], type = "class")
table(pred = pred, true = OJ$Purchase[!train])
          true
pred  CH  MM
  CH 160  38
  MM   8  64

      The test error rate is 0.226.

    6. set.seed(1)
OJ.cv <- cv.tree(OJ.tree, FUN = prune.misclass)
    7. plot(OJ.cv$size, OJ.cv$dev, type = "l")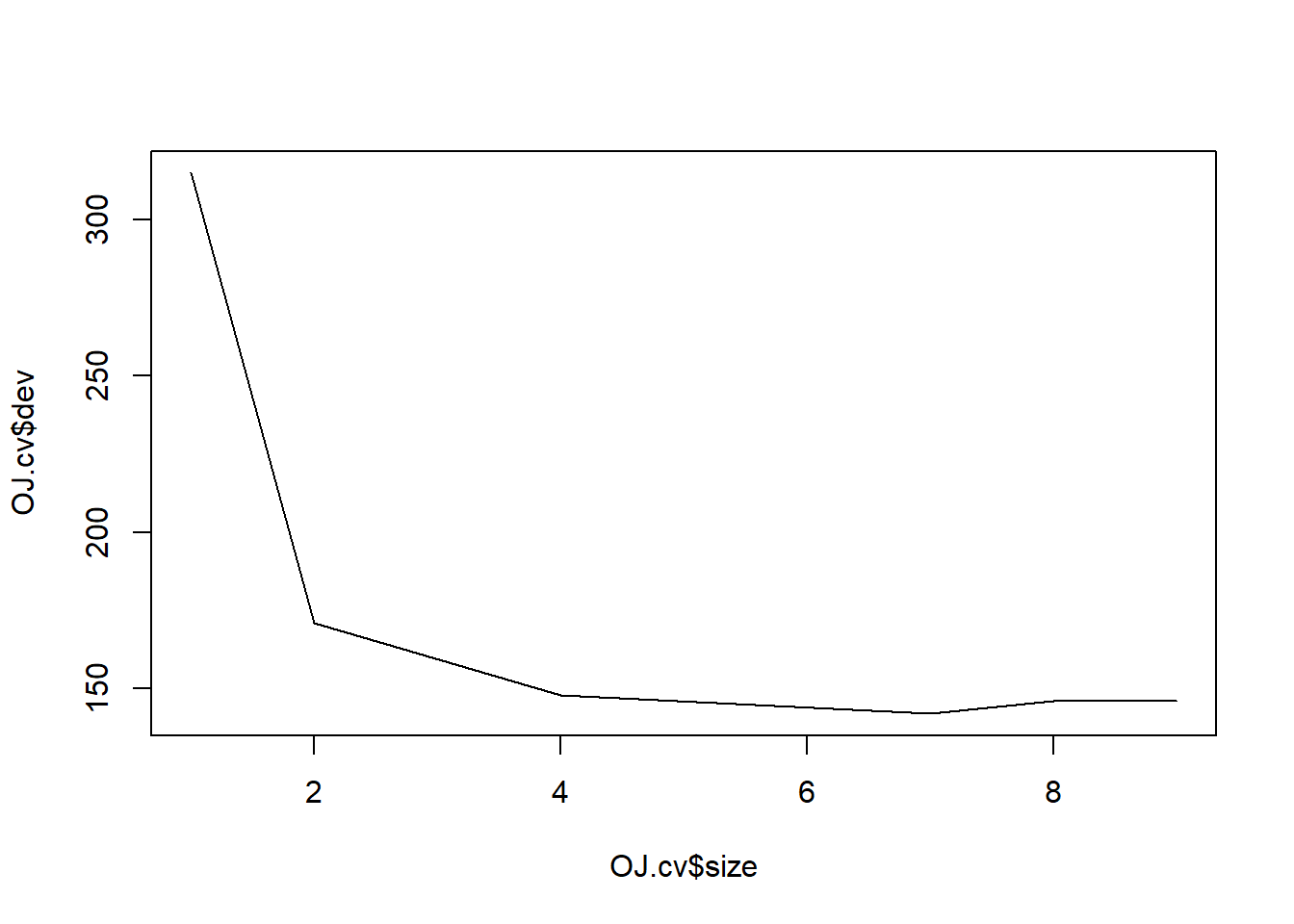

      The optimal-sized tree has 7 leaves (aka terminal nodes).

    8. See (g)

    9. OJ.prune <- prune.misclass(OJ.tree, best = 5)
    10. table(fitted = predict(OJ.prune, type = "class"), true = OJ$Purchase[train])
            true
fitted  CH  MM
    CH 441  86
    MM  44 229
      table(fitted = predict(OJ.tree, type = "class"), true = OJ$Purchase[train])
            true
fitted  CH  MM
    CH 450  92
    MM  35 223

      The training error is the same! (But could we have known this previously?) Look at the statistics in OJ.cv.

    11. pred.prune <- predict(OJ.prune, newdata = OJ[!train, ], type = "class")
table(pred = pred.prune, true = OJ$Purchase[!train])
          true
pred  CH  MM
  CH 160  36
  MM   8  66
      pred.tree <- predict(OJ.tree, newdata = OJ[!train, ], type = "class")
table(pred = pred.tree, true = OJ$Purchase[!train])
          true
pred  CH  MM
  CH 160  38
  MM   8  64

      The test error is also the same here.

  3. Question

    1. library(ISLR2)
myHitters <- Hitters[!is.na(Hitters$Salary), ]
myHitters$Salary <- log(myHitters$Salary)
    2. train <- c(rep(TRUE, 200), rep(FALSE, nrow(myHitters) - 200))
    3. library(gbm)
      Loaded gbm 2.2.2
      This version of gbm is no longer under development. Consider transitioning to gbm3, https://github.com/gbm-developers/gbm3
      set.seed(1)
lambda <- 10^seq(-5, -0.2, by = 0.05)
trainMSE <- rep(Inf, length(lambda))
testMSE <- rep(Inf, length(lambda))
for (i in 1:length(lambda)) {
  fit <- gbm(Salary ~ .,
    distribution = "gaussian", data = myHitters[train, ],
    n.trees = 1000, shrinkage = lambda[i]
  )
  pred.train <- predict(fit, n.trees = 1000)
  pred.test <- predict(fit, newdata = myHitters[!train, ], n.trees = 1000)
  trainMSE[i] <- mean((myHitters$Salary[train] - pred.train)^2)
  testMSE[i] <- mean((myHitters$Salary[!train] - pred.test)^2)
}
plot(lambda, trainMSE, type = "l")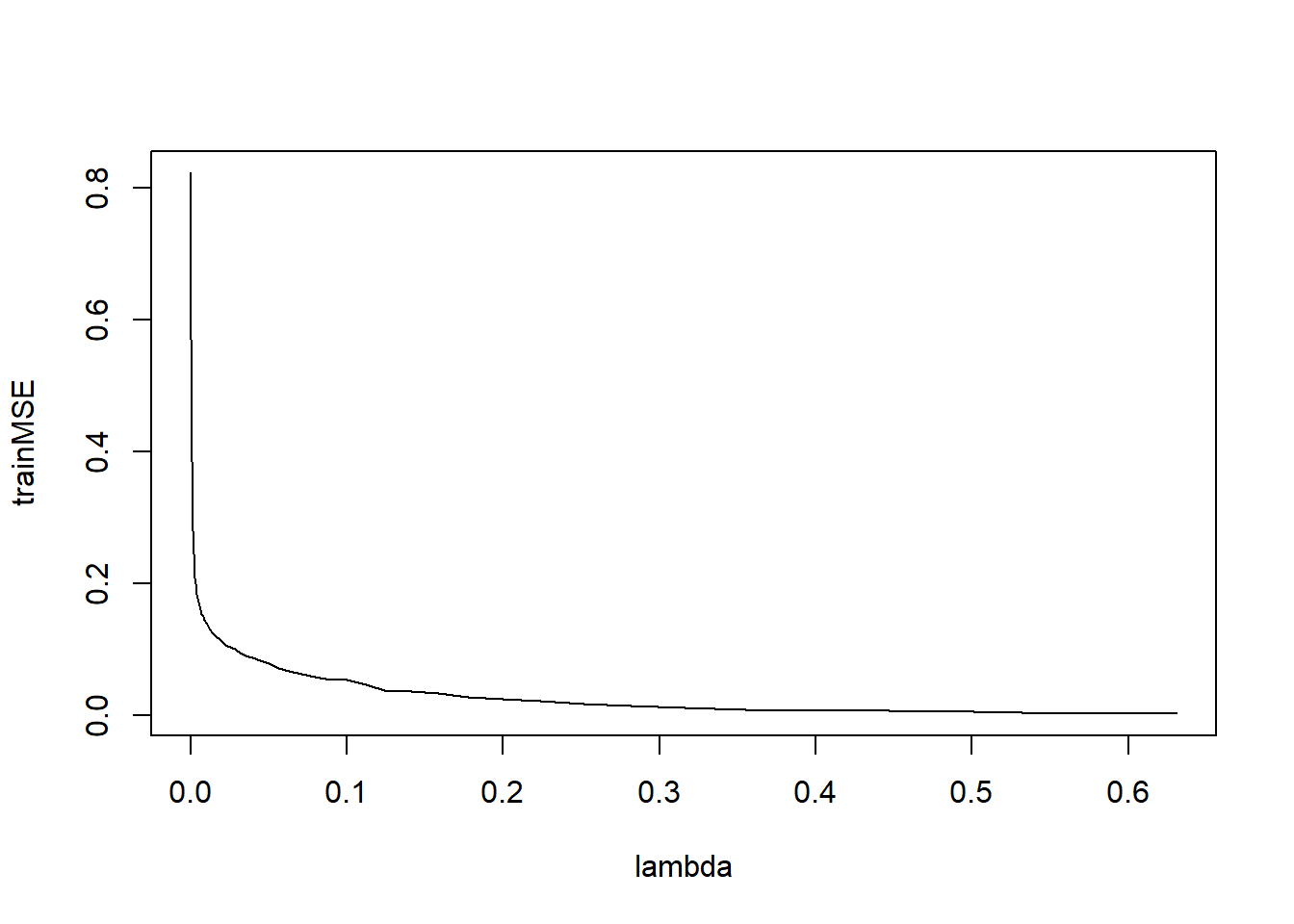

      plot(lambda, testMSE, type = "l")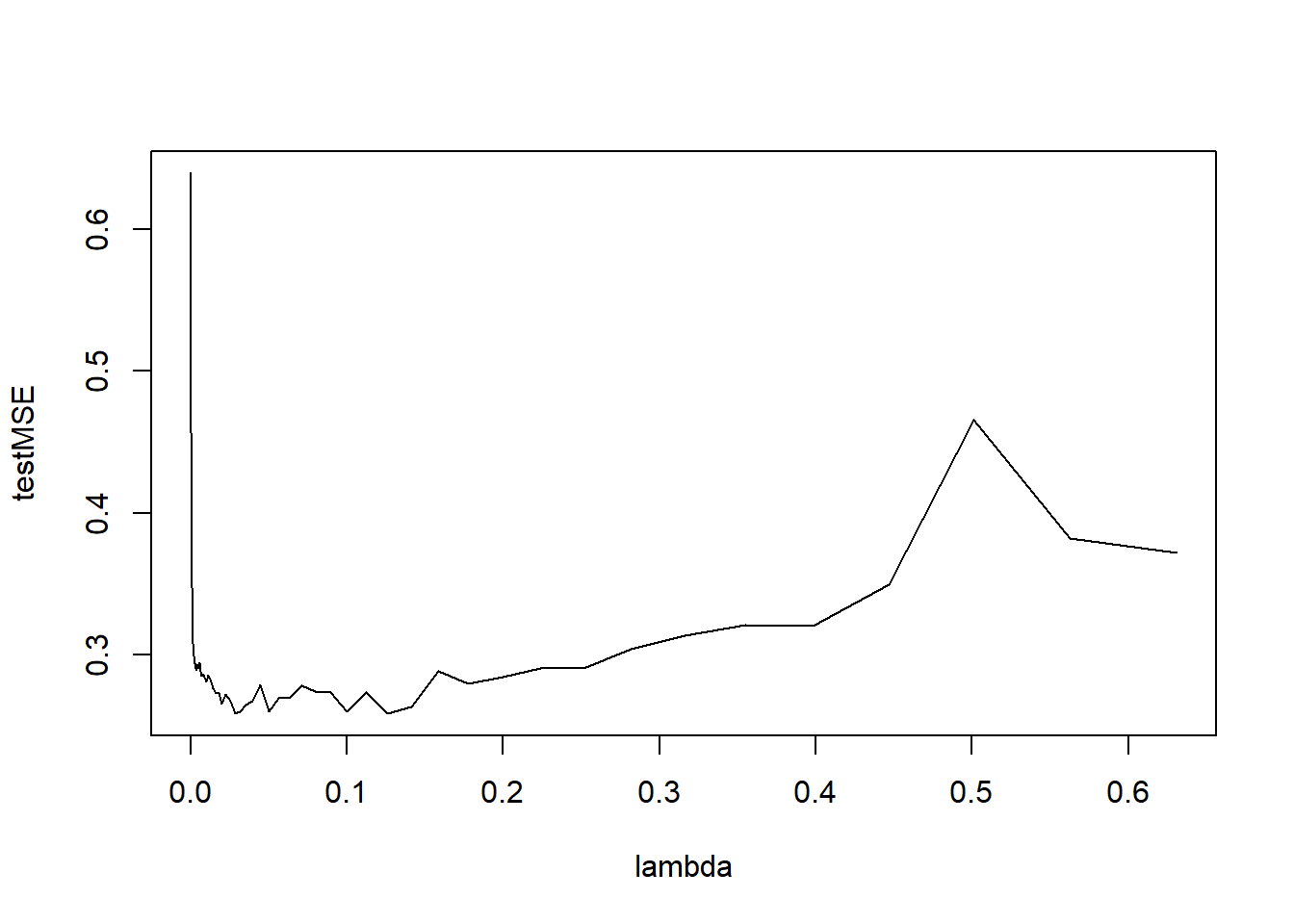

    4. See (c)

    5. library(MASS)
      
Attaching package: 'MASS'
      The following object is masked from 'package:ISLR2':

    Boston
      myHitters.lm <- stepAIC(lm(Salary ~ ., data = myHitters, subset = train),
  direction = "both"
)
      Start:  AIC=-187.65
Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + Years + 
    CAtBat + CHits + CHmRun + CRuns + CRBI + CWalks + League + 
    Division + PutOuts + Assists + Errors + NewLeague

            Df Sum of Sq    RSS     AIC
- CHmRun     1    0.0049 64.080 -189.64
- NewLeague  1    0.0129 64.088 -189.61
- CRBI       1    0.0220 64.097 -189.59
- Runs       1    0.0709 64.146 -189.43
- RBI        1    0.0751 64.150 -189.42
- CAtBat     1    0.0958 64.171 -189.35
- HmRun      1    0.1761 64.251 -189.10
- CHits      1    0.2560 64.331 -188.86
- League     1    0.2878 64.362 -188.76
- Errors     1    0.3521 64.427 -188.56
<none>                   64.075 -187.65
- Division   1    0.8491 64.924 -187.02
- CRuns      1    0.8673 64.942 -186.97
- Assists    1    1.0963 65.171 -186.26
- CWalks     1    1.9086 65.983 -183.78
- Years      1    2.4861 66.561 -182.04
- AtBat      1    2.5729 66.648 -181.78
- Walks      1    2.8898 66.964 -180.83
- PutOuts    1    3.2769 67.352 -179.68
- Hits       1    4.3240 68.399 -176.59

Step:  AIC=-189.64
Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + Years + 
    CAtBat + CHits + CRuns + CRBI + CWalks + League + Division + 
    PutOuts + Assists + Errors + NewLeague

            Df Sum of Sq    RSS     AIC
- NewLeague  1    0.0119 64.092 -191.60
- RBI        1    0.0875 64.167 -191.37
- Runs       1    0.0891 64.169 -191.36
- CAtBat     1    0.1110 64.191 -191.29
- HmRun      1    0.2377 64.317 -190.90
- League     1    0.2838 64.363 -190.75
- CRBI       1    0.3051 64.385 -190.69
- Errors     1    0.3510 64.431 -190.55
- CHits      1    0.5538 64.633 -189.92
<none>                   64.080 -189.64
- Division   1    0.8580 64.938 -188.98
- Assists    1    1.0914 65.171 -188.26
+ CHmRun     1    0.0049 64.075 -187.65
- CRuns      1    1.6078 65.687 -186.68
- CWalks     1    2.1324 66.212 -185.09
- Years      1    2.4813 66.561 -184.04
- AtBat      1    2.5702 66.650 -183.77
- Walks      1    2.9502 67.030 -182.64
- PutOuts    1    3.2741 67.354 -181.67
- Hits       1    4.4492 68.529 -178.21

Step:  AIC=-191.6
Salary ~ AtBat + Hits + HmRun + Runs + RBI + Walks + Years + 
    CAtBat + CHits + CRuns + CRBI + CWalks + League + Division + 
    PutOuts + Assists + Errors

            Df Sum of Sq    RSS     AIC
- Runs       1    0.0852 64.177 -193.34
- RBI        1    0.0870 64.179 -193.33
- CAtBat     1    0.1133 64.205 -193.25
- HmRun      1    0.2378 64.329 -192.86
- CRBI       1    0.3133 64.405 -192.63
- Errors     1    0.3435 64.435 -192.53
- CHits      1    0.5746 64.666 -191.82
<none>                   64.092 -191.60
- League     1    0.6500 64.742 -191.58
- Division   1    0.8610 64.953 -190.93
- Assists    1    1.0989 65.190 -190.20
+ NewLeague  1    0.0119 64.080 -189.64
+ CHmRun     1    0.0040 64.088 -189.61
- CRuns      1    1.6393 65.731 -188.55
- CWalks     1    2.1279 66.219 -187.07
- Years      1    2.4904 66.582 -185.98
- AtBat      1    2.6070 66.699 -185.63
- Walks      1    2.9386 67.030 -184.63
- PutOuts    1    3.2764 67.368 -183.63
- Hits       1    4.4593 68.551 -180.15

Step:  AIC=-193.34
Salary ~ AtBat + Hits + HmRun + RBI + Walks + Years + CAtBat + 
    CHits + CRuns + CRBI + CWalks + League + Division + PutOuts + 
    Assists + Errors

            Df Sum of Sq    RSS     AIC
- RBI        1    0.0618 64.239 -195.14
- CAtBat     1    0.0870 64.264 -195.06
- HmRun      1    0.1634 64.340 -194.83
- Errors     1    0.3273 64.504 -194.32
- CRBI       1    0.4024 64.579 -194.09
- CHits      1    0.4926 64.669 -193.81
<none>                   64.177 -193.34
- League     1    0.7004 64.877 -193.16
- Division   1    0.8457 65.022 -192.72
- Assists    1    1.1085 65.285 -191.91
+ Runs       1    0.0852 64.092 -191.60
+ CHmRun     1    0.0208 64.156 -191.40
+ NewLeague  1    0.0080 64.169 -191.36
- CRuns      1    1.6598 65.837 -190.23
- CWalks     1    2.0465 66.223 -189.06
- Years      1    2.5245 66.701 -187.62
- AtBat      1    2.6071 66.784 -187.37
- Walks      1    3.0973 67.274 -185.91
- PutOuts    1    3.3751 67.552 -185.08
- Hits       1    5.2867 69.463 -179.50

Step:  AIC=-195.14
Salary ~ AtBat + Hits + HmRun + Walks + Years + CAtBat + CHits + 
    CRuns + CRBI + CWalks + League + Division + PutOuts + Assists + 
    Errors

            Df Sum of Sq    RSS     AIC
- HmRun      1    0.1074 64.346 -196.81
- CAtBat     1    0.1121 64.351 -196.79
- Errors     1    0.3404 64.579 -196.09
- CRBI       1    0.3411 64.580 -196.08
- CHits      1    0.5728 64.811 -195.37
<none>                   64.239 -195.14
- League     1    0.6842 64.923 -195.02
- Division   1    0.8171 65.056 -194.62
- Assists    1    1.1172 65.356 -193.69
+ RBI        1    0.0618 64.177 -193.34
+ Runs       1    0.0600 64.179 -193.33
+ CHmRun     1    0.0332 64.205 -193.25
+ NewLeague  1    0.0082 64.230 -193.17
- CRuns      1    1.8768 66.115 -191.38
- CWalks     1    2.0449 66.283 -190.88
- Years      1    2.5017 66.740 -189.50
- AtBat      1    2.8465 67.085 -188.47
- Walks      1    3.0732 67.312 -187.80
- PutOuts    1    3.4528 67.691 -186.67
- Hits       1    5.2334 69.472 -181.48

Step:  AIC=-196.81
Salary ~ AtBat + Hits + Walks + Years + CAtBat + CHits + CRuns + 
    CRBI + CWalks + League + Division + PutOuts + Assists + Errors

            Df Sum of Sq    RSS     AIC
- CAtBat     1    0.1313 64.477 -198.40
- Errors     1    0.3031 64.649 -197.87
- CRBI       1    0.6032 64.949 -196.94
- League     1    0.6451 64.991 -196.81
<none>                   64.346 -196.81
- CHits      1    0.7286 65.075 -196.56
- Division   1    0.8421 65.188 -196.21
- Assists    1    1.0108 65.357 -195.69
+ HmRun      1    0.1074 64.239 -195.14
+ CHmRun     1    0.0722 64.274 -195.03
+ NewLeague  1    0.0108 64.335 -194.84
+ Runs       1    0.0074 64.339 -194.83
+ RBI        1    0.0058 64.340 -194.83
- CRuns      1    2.0625 66.408 -192.50
- CWalks     1    2.1395 66.485 -192.27
- Years      1    2.4855 66.831 -191.23
- AtBat      1    2.7484 67.094 -190.44
- Walks      1    3.1563 67.502 -189.23
- PutOuts    1    3.4623 67.808 -188.33
- Hits       1    5.3023 69.648 -182.97

Step:  AIC=-198.4
Salary ~ AtBat + Hits + Walks + Years + CHits + CRuns + CRBI + 
    CWalks + League + Division + PutOuts + Assists + Errors

            Df Sum of Sq    RSS     AIC
- Errors     1    0.3400 64.817 -199.35
<none>                   64.477 -198.40
- League     1    0.6931 65.170 -198.26
- CRBI       1    0.7669 65.244 -198.04
- Division   1    0.8264 65.304 -197.85
- CHits      1    1.0305 65.508 -197.23
+ CAtBat     1    0.1313 64.346 -196.81
+ HmRun      1    0.1266 64.351 -196.79
+ CHmRun     1    0.1138 64.363 -196.75
- Assists    1    1.2204 65.698 -196.65
+ NewLeague  1    0.0145 64.463 -196.45
+ RBI        1    0.0038 64.473 -196.41
+ Runs       1    0.0002 64.477 -196.40
- CRuns      1    1.9601 66.437 -194.41
- CWalks     1    2.0480 66.525 -194.15
- AtBat      1    2.7199 67.197 -192.14
- Walks      1    3.0259 67.503 -191.23
- PutOuts    1    3.3495 67.827 -190.27
- Years      1    3.9323 68.410 -188.56
- Hits       1    5.4618 69.939 -184.14

Step:  AIC=-199.35
Salary ~ AtBat + Hits + Walks + Years + CHits + CRuns + CRBI + 
    CWalks + League + Division + PutOuts + Assists

            Df Sum of Sq    RSS     AIC
- League     1    0.6153 65.433 -199.46
<none>                   64.817 -199.35
- CRBI       1    0.7184 65.536 -199.14
- Division   1    0.8639 65.681 -198.70
- Assists    1    0.9112 65.728 -198.56
+ Errors     1    0.3400 64.477 -198.40
- CHits      1    1.0614 65.879 -198.10
+ CAtBat     1    0.1683 64.649 -197.87
+ CHmRun     1    0.1027 64.715 -197.67
+ HmRun      1    0.0859 64.731 -197.61
+ NewLeague  1    0.0062 64.811 -197.37
+ RBI        1    0.0000 64.817 -197.35
+ Runs       1    0.0000 64.817 -197.35
- CWalks     1    1.9827 66.800 -195.32
- CRuns      1    1.9910 66.808 -195.30
- AtBat      1    3.0871 67.904 -192.04
- Walks      1    3.1044 67.922 -191.99
- PutOuts    1    3.3522 68.169 -191.26
- Years      1    4.1178 68.935 -189.03
- Hits       1    5.9080 70.725 -183.90

Step:  AIC=-199.46
Salary ~ AtBat + Hits + Walks + Years + CHits + CRuns + CRBI + 
    CWalks + Division + PutOuts + Assists

            Df Sum of Sq    RSS     AIC
- CRBI       1    0.6392 66.072 -199.51
<none>                   65.433 -199.46
+ League     1    0.6153 64.817 -199.35
- Division   1    0.8091 66.242 -199.00
- CHits      1    0.8163 66.249 -198.98
+ NewLeague  1    0.3785 65.054 -198.62
- Assists    1    0.9543 66.387 -198.56
+ Errors     1    0.2622 65.170 -198.26
+ CAtBat     1    0.2134 65.219 -198.11
+ CHmRun     1    0.0934 65.339 -197.75
+ HmRun      1    0.0579 65.375 -197.64
+ Runs       1    0.0075 65.425 -197.48
+ RBI        1    0.0006 65.432 -197.46
- CRuns      1    1.7237 67.156 -196.26
- CWalks     1    1.8619 67.294 -195.85
- AtBat      1    3.2103 68.643 -191.88
- Walks      1    3.3974 68.830 -191.34
- PutOuts    1    3.4478 68.880 -191.19
- Years      1    3.8438 69.276 -190.04
- Hits       1    5.7897 71.222 -184.50

Step:  AIC=-199.52
Salary ~ AtBat + Hits + Walks + Years + CHits + CRuns + CWalks + 
    Division + PutOuts + Assists

            Df Sum of Sq    RSS     AIC
- CHits      1    0.5086 66.580 -199.98
+ CHmRun     1    0.7324 65.339 -199.74
- Assists    1    0.6552 66.727 -199.54
<none>                   66.072 -199.51
+ CRBI       1    0.6392 65.433 -199.46
+ League     1    0.5361 65.536 -199.14
- Division   1    0.8042 66.876 -199.09
+ CAtBat     1    0.3820 65.690 -198.68
+ HmRun      1    0.3080 65.764 -198.45
+ NewLeague  1    0.2843 65.787 -198.38
+ Errors     1    0.2266 65.845 -198.20
+ RBI        1    0.1568 65.915 -197.99
+ Runs       1    0.0180 66.054 -197.57
- CWalks     1    1.5544 67.626 -196.87
- CRuns      1    1.8017 67.873 -196.13
- AtBat      1    2.9686 69.040 -192.72
- Walks      1    3.3606 69.432 -191.59
- PutOuts    1    3.5426 69.614 -191.07
- Years      1    4.1936 70.265 -189.21
- Hits       1    5.6890 71.761 -185.00

Step:  AIC=-199.98
Salary ~ AtBat + Hits + Walks + Years + CRuns + CWalks + Division + 
    PutOuts + Assists

            Df Sum of Sq    RSS     AIC
+ CHmRun     1    0.9592 65.621 -200.88
- Assists    1    0.4404 67.021 -200.66
<none>                   66.580 -199.98
+ CHits      1    0.5086 66.072 -199.51
+ HmRun      1    0.4522 66.128 -199.34
+ League     1    0.3603 66.220 -199.07
+ CRBI       1    0.3316 66.249 -198.98
+ Errors     1    0.2653 66.315 -198.78
- Division   1    1.1221 67.703 -198.64
+ RBI        1    0.1526 66.428 -198.44
- CWalks     1    1.1927 67.773 -198.43
+ NewLeague  1    0.1262 66.454 -198.36
+ CAtBat     1    0.0864 66.494 -198.24
+ Runs       1    0.0508 66.530 -198.13
- CRuns      1    2.4724 69.053 -194.69
- AtBat      1    2.6054 69.186 -194.30
- PutOuts    1    3.1307 69.711 -192.79
- Walks      1    3.7084 70.289 -191.14
- Years      1    3.7734 70.354 -190.96
- Hits       1    5.2100 71.790 -186.91

Step:  AIC=-200.88
Salary ~ AtBat + Hits + Walks + Years + CRuns + CWalks + Division + 
    PutOuts + Assists + CHmRun

            Df Sum of Sq    RSS     AIC
<none>                   65.621 -200.88
+ League     1    0.4883 65.133 -200.38
- Assists    1    0.8610 66.482 -200.28
- CHmRun     1    0.9592 66.580 -199.98
+ Errors     1    0.3065 65.315 -199.82
- Division   1    1.0239 66.645 -199.79
+ CHits      1    0.2818 65.339 -199.74
+ NewLeague  1    0.2366 65.385 -199.61
+ CRBI       1    0.1907 65.430 -199.47
+ CAtBat     1    0.0667 65.555 -199.09
+ HmRun      1    0.0422 65.579 -199.01
+ Runs       1    0.0383 65.583 -199.00
+ RBI        1    0.0157 65.606 -198.93
- CWalks     1    1.5295 67.151 -198.28
- CRuns      1    1.6423 67.263 -197.94
- AtBat      1    3.0894 68.711 -193.68
- PutOuts    1    3.1887 68.810 -193.39
- Years      1    3.7086 69.330 -191.89
- Walks      1    3.7259 69.347 -191.84
- Hits       1    5.6581 71.279 -186.34
      set.seed(1)
require(glmnet)
      Loading required package: glmnet
      Loading required package: Matrix
      Loaded glmnet 4.1-8
      myHitters.cv <- cv.glmnet(model.matrix(Salary ~ ., data = myHitters[train, ]),
  myHitters$Salary[train],
  alpha = 1
)
myHitters.lasso <- glmnet(model.matrix(Salary ~ ., data = myHitters[train, ]),
  myHitters$Salary[train],
  alpha = 1
)
myHitters.pred.lasso <- predict(myHitters.lasso,
  type = "response",
  newx = model.matrix(Salary ~ .,
    data = myHitters[!train, ]
  )
)
myHitters.pred.lm <- predict(myHitters.lm, newdata = myHitters[!train, ])
mean((myHitters.pred.lasso - myHitters$Salary[!train])^2)
      [1] 0.4755605
      mean((myHitters.pred.lm - myHitters$Salary[!train])^2)
      [1] 0.4931775

      The MSE’s of the linear model and the lasso model seem to be higher than the MSE of the boosted model except for larger values of \lambda.

    6. summary(fit)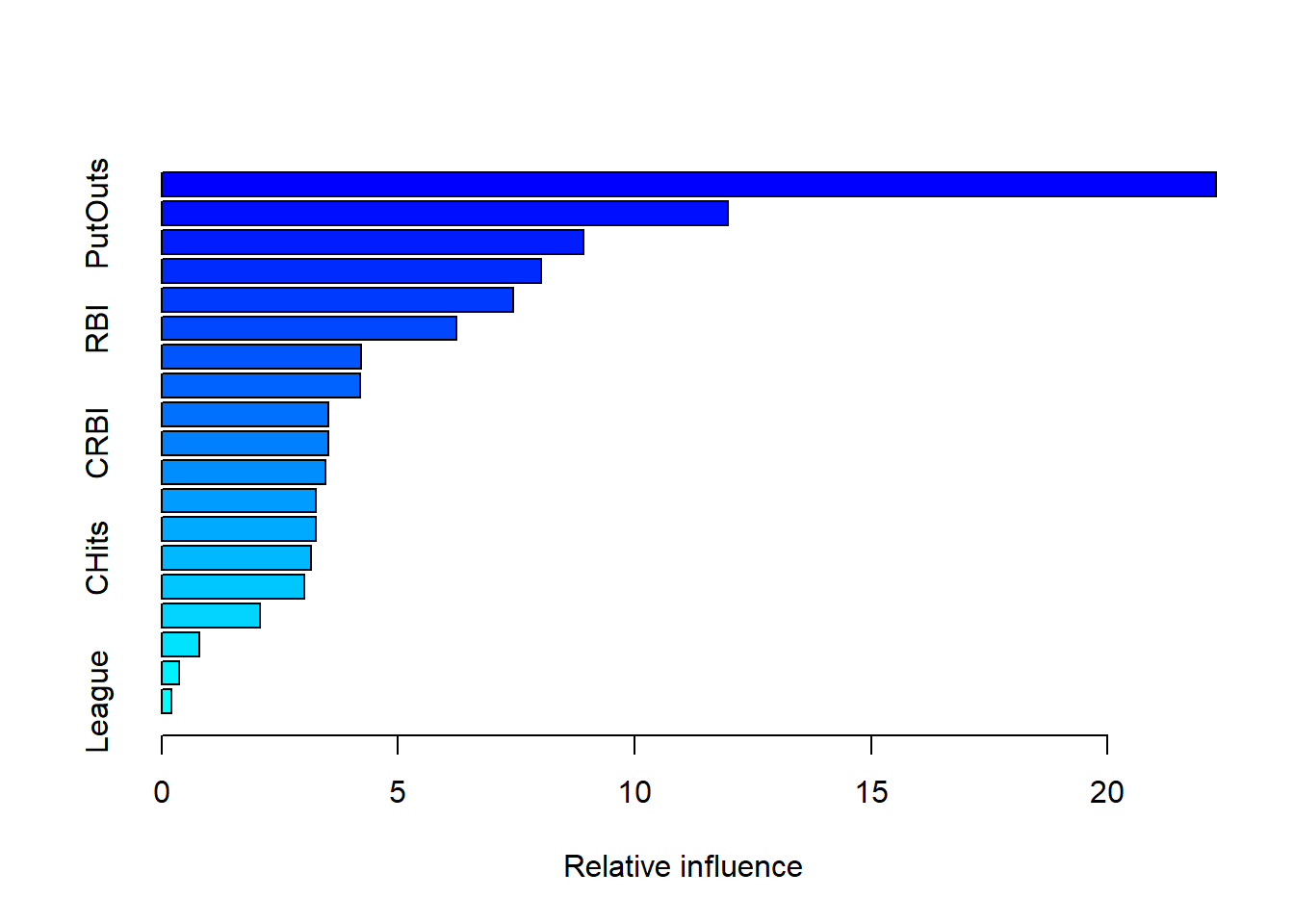

      CAtBat and PutOuts appear to be the most important outputs.

    7. library(randomForest)
set.seed(1)
myHitters.bag <- randomForest(Salary ~ .,
  data = myHitters, subset = train,
  mtry = (ncol(myHitters) - 1), importance = TRUE
)
pred <- predict(myHitters.bag, newdata = myHitters[!train, ])
mean((myHitters$Salary[!train] - pred)^2)
      [1] 0.2301184

      The test MSE is 0.229, which is lower than the minimum test MSE from the boosted model.