Machine Learning: Cross-Validation & Regularisation

library(tidyverse)
library(rpart)
library(rpart.plot)
library(glmnet)

Overview

• A regression recap from a machine learning perspective
• Model comparison with validation sets
  • Validation Set Approach
  • k-Fold Cross-Validation
  • Leave-One-Out Cross-Validation
• Regularisation
  • Ridge Regression
  • Lasso Regression

Linear Regression Recap

Single Linear Regression (SLR)

Scenario: use head circumference (mm) to predict age (weeks) of a fetal baby

\boldsymbol{x} = \begin{pmatrix} 105 \\ 120 \\ 110 \\ 117 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 20 \\ 24 \\ 22 \\ 23 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 20.3 \\ 24.0 \\ 21.5 \\ 23.2 \\ \end{pmatrix}

\hat{y}(x) = \beta_0 + \beta_1 x

circumference <- c(105, 120, 110, 117)
age <- c(20, 24, 22, 23)
model <- lm(age ~ circumference)
print(coef(model))

  (Intercept) circumference 
   -5.5905797     0.2463768 

predict(model, newdata = data.frame(circumference))

       1        2        3        4 
20.27899 23.97464 21.51087 23.23551 

Mean squared error

\boldsymbol{y} = \begin{pmatrix} 20 \\ 24 \\ 22 \\ 23 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 20.3 \\ 24.0 \\ 21.5 \\ 23.2 \\ \end{pmatrix}, \quad \boldsymbol{y} - \hat{\boldsymbol{y}} = \begin{pmatrix} -0.3 \\ 0 \\ 0.5 \\ -0.2 \\ \end{pmatrix}.

# Predictions
predicted_age <- predict(model, newdata = data.frame(circumference = circumference))

# Calculate ranges
x_range <- max(circumference) - min(circumference)
y_range <- max(age) - min(age)

# Calculate optimal aspect ratio
optimal_aspect_ratio <- x_range / y_range

# Create data frame for plotting
data <- data.frame(circumference, age, predicted_age)
data$error <- abs(data$age - data$predicted_age)

mse <- mean(data$error^2)

# Plotting
ggplot(data, aes(x = circumference, y = age)) +
  geom_point() +
  geom_line(aes(y = predicted_age)) +
  geom_segment(aes(xend = circumference, yend = predicted_age), linetype = 'dashed') +
  geom_rect(aes(xmin = circumference, xmax = circumference + error, ymin = pmin(age, predicted_age), ymax = pmin(age, predicted_age) + error),
            fill = 'red', alpha = 0.3) +
  xlab('Head Circumference (mm)') +
  ylab('Age (weeks)') +
  theme_minimal() +
  theme(aspect.ratio = 1 / optimal_aspect_ratio) +
  theme(legend.position = 'none') +
  ggtitle(paste('MSE = ', round(mse, 2)))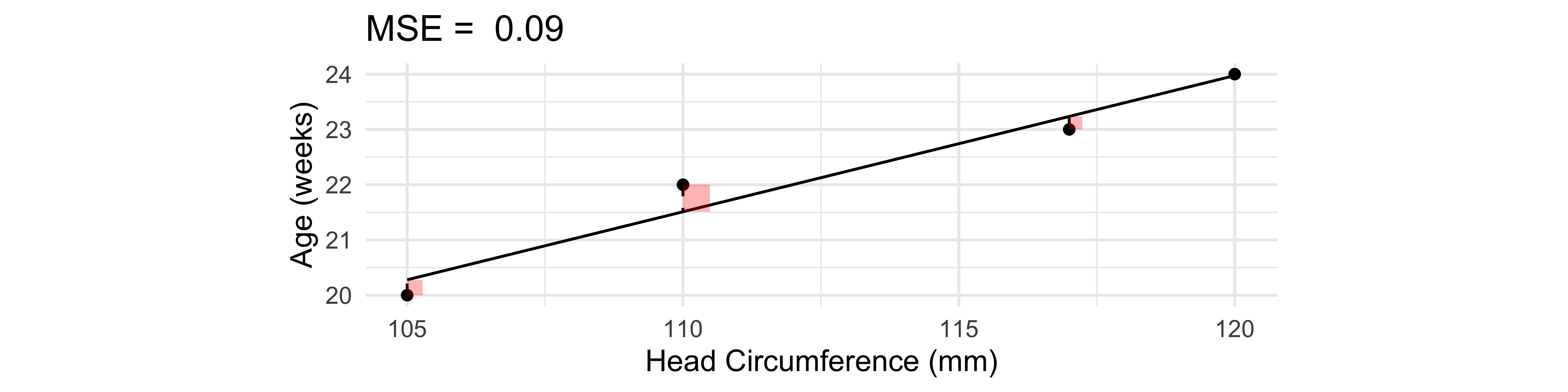

\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \frac{1}{4} \Bigl[ (-0.3)^2 + 0^2 + 0.5^2 + (-0.2)^2 \Bigr] = 0.09.

\text{RSS} = \sum_{i=1}^n (y_i - \hat{y}_i)^2 = 0.38.

Sensitive to outliers

\text{If we instead had } \boldsymbol{y} = \begin{pmatrix} \textcolor{red}{10} & 24 & 22 & 23 \end{pmatrix}^\top.

circumference <- c(105, 120, 110, 117)
age <- c(10, 24, 22, 23)
new_model <- lm(age ~ circumference)

# Predictions
predicted_age <- predict(model, newdata = data.frame(circumference = circumference))

# Calculate ranges
x_range <- max(circumference) - min(circumference)
y_range <- max(age) - min(age)

# Calculate optimal aspect ratio
optimal_aspect_ratio <- x_range / y_range

# Create data frame for plotting
data <- data.frame(circumference, age, predicted_age)
data$error <- abs(data$age - data$predicted_age)

mse <- mean(data$error^2)

# Plotting
ggplot(data, aes(x = circumference, y = age)) +
  geom_point() +
  geom_line(aes(y = predicted_age)) +
  geom_segment(aes(xend = circumference, yend = predicted_age), linetype = 'dashed') +
  geom_rect(aes(xmin = circumference, xmax = circumference + error, ymin = pmin(age, predicted_age), ymax = pmin(age, predicted_age) + error),
            fill = 'red', alpha = 0.3) +
  xlab('Head Circumference (mm)') +
  ylab('Age (weeks)') +
  theme_minimal() +
  theme(aspect.ratio = 1 / optimal_aspect_ratio) +
  theme(legend.position = 'none') + 
  ggtitle(paste('MSE = ', round(mse, 2)))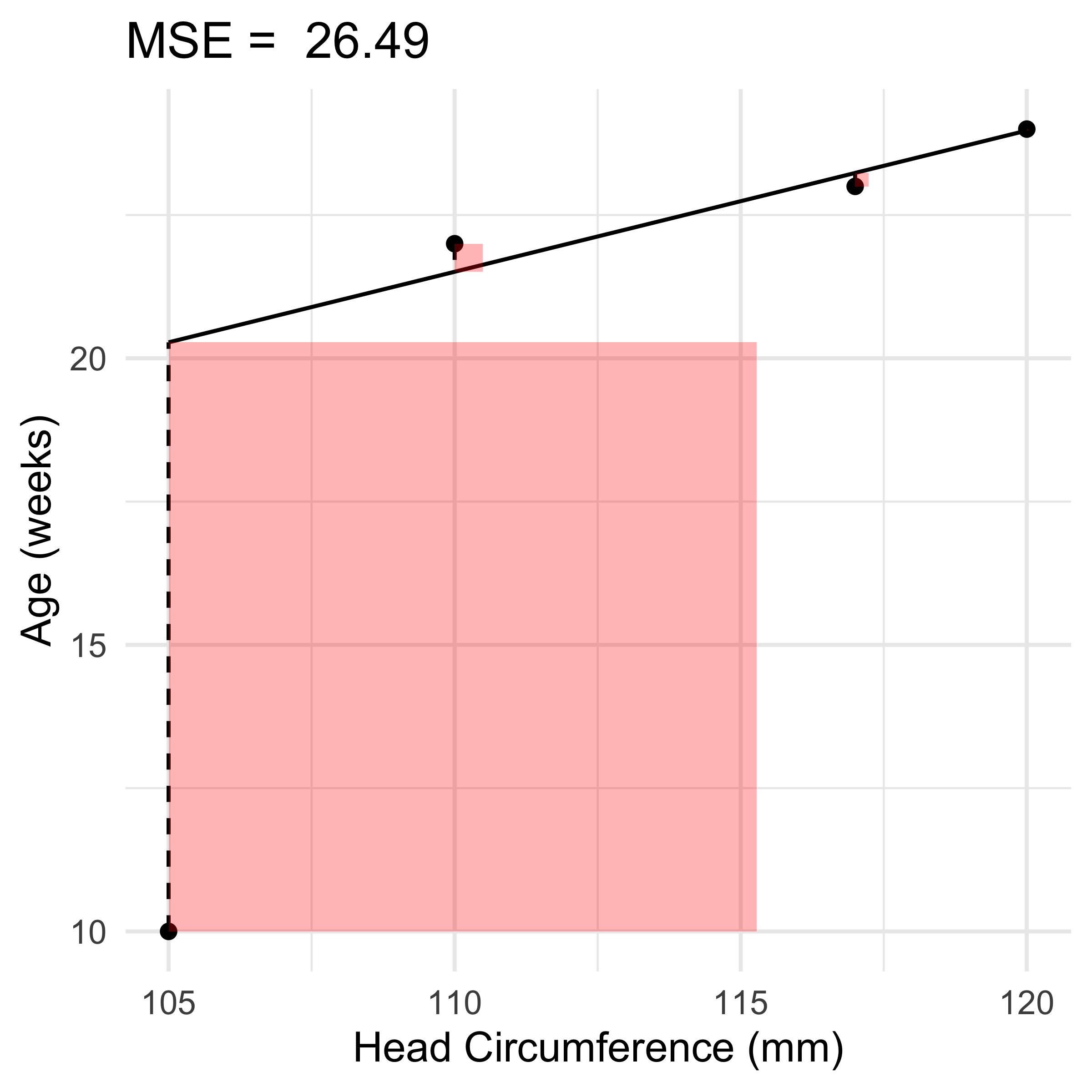

The previous model

new_model <- lm(age ~ circumference)

# Predictions
predicted_age <- predict(new_model, newdata = data.frame(circumference = circumference))

# Calculate ranges
x_range <- max(circumference) - min(circumference)
y_range <- max(age) - min(age)

# Calculate optimal aspect ratio
optimal_aspect_ratio <- x_range / y_range

# Create data frame for plotting
data <- data.frame(circumference, age, predicted_age)
data$error <- abs(data$age - data$predicted_age)

mse <- mean(data$error^2)

# Plotting
ggplot(data, aes(x = circumference, y = age)) +
  geom_point() +
  geom_line(aes(y = predicted_age)) +
  geom_segment(aes(xend = circumference, yend = predicted_age), linetype = 'dashed') +
  geom_rect(aes(xmin = circumference, xmax = circumference + error, ymin = pmin(age, predicted_age), ymax = pmin(age, predicted_age) + error),
            fill = 'red', alpha = 0.3) +
  xlab('Head Circumference (mm)') +
  ylab('Age (weeks)') +
  theme_minimal() +
  theme(aspect.ratio = 1 / optimal_aspect_ratio) +
  theme(legend.position = 'none') +
  ggtitle(paste('MSE = ', round(mse, 2)))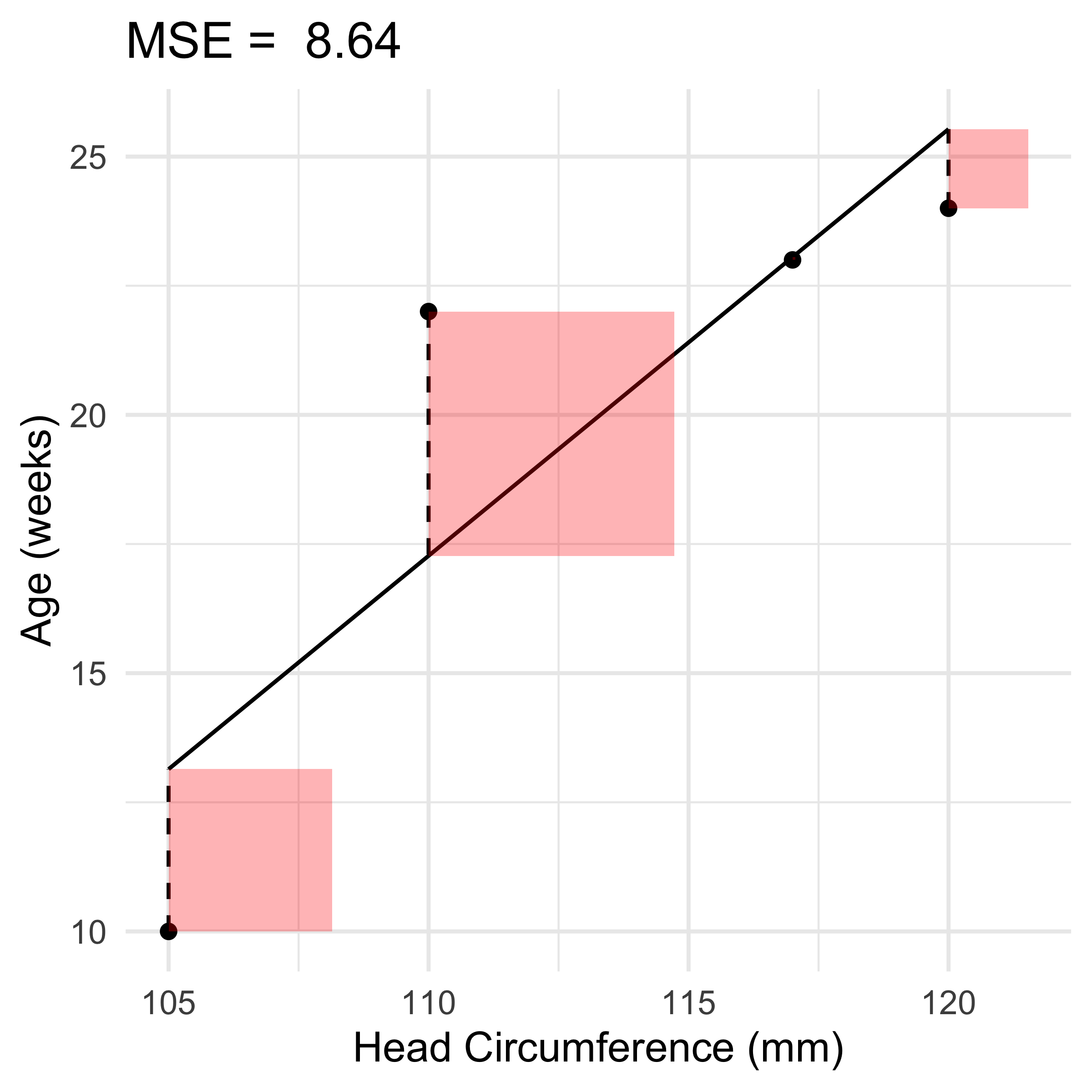

New model after training

Multiple Linear Regression (MLR)

Scenario: use temperature (^\circ C) and humidity (%) to predict rainfall (mm)

\boldsymbol{X} = \begin{pmatrix} 27 & 80 \\ 32 & 70 \\ 28 & 72 \\ 22 & 86 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 6 \\ 7 \\ 6 \\ 4 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 5.7 \\ 7.2 \\ 5.9 \\ 4.2 \\ \end{pmatrix}

\hat{y}(\boldsymbol{x}) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p = \beta_0 + \left \langle \boldsymbol{\beta}, \boldsymbol{x} \right \rangle

weather <- data.frame(temperature = c(27, 32, 28, 22), humidity = c(80, 70, 72, 86))
rainfall <- c(6, 7, 6, 4)
model <- lm(rainfall ~ temperature + humidity, data = weather)
summary(model)$coefficients

               Estimate  Std. Error    t value  Pr(>|t|)
(Intercept) -5.51001821 10.45422801 -0.5270612 0.6912003
temperature  0.34244080  0.15162225  2.2585129 0.2653588
humidity     0.02504554  0.08434494  0.2969418 0.8162405

predict(model, newdata = weather)

       1        2        3        4 
5.739526 7.201275 5.881603 4.177596 

MLR’s design matrix

Scenario: use temperature (^\circ C) and humidity (%) to predict rainfall (mm)

\boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 27 & 80 \\ \textcolor{grey}{1} & 32 & 70 \\ \textcolor{grey}{1} & 28 & 72 \\ \textcolor{grey}{1} & 22 & 86 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 6 \\ 7 \\ 6 \\ 4 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 5.7 \\ 7.2 \\ 5.9 \\ 4.2 \\ \end{pmatrix}

\hat{y}(\boldsymbol{x}) = \beta_0 x_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p = \langle \boldsymbol{\beta}, \boldsymbol{x} \rangle

as.matrix(weather)

     temperature humidity
[1,]          27       80
[2,]          32       70
[3,]          28       72
[4,]          22       86

X <- model.matrix(rainfall ~ temperature + humidity, data = weather)
X

  (Intercept) temperature humidity
1           1          27       80
2           1          32       70
3           1          28       72
4           1          22       86
attr(,"assign")
[1] 0 1 2

MLR is just matrix equations

\boldsymbol{\beta} = (\boldsymbol{X}^\top\boldsymbol{X})^{-1} \boldsymbol{X}^\top \boldsymbol{y}

model <- lm(rainfall ~ temperature +
        humidity, data = weather)
coef(model)

(Intercept) temperature    humidity 
-5.51001821  0.34244080  0.02504554 

y <- rainfall
beta <- solve(t(X) %*% X) %*% t(X) %*% y
beta

                   [,1]
(Intercept) -5.51001821
temperature  0.34244080
humidity     0.02504554

\hat{\boldsymbol{y}} = \boldsymbol{X} \boldsymbol{\beta}.

predict(model, newdata = weather)

       1        2        3        4 
5.739526 7.201275 5.881603 4.177596 

X %*% beta

      [,1]
1 5.739526
2 7.201275
3 5.881603
4 4.177596

MLR after normalising the inputs

Scenario: use temperature (z-score) and humidity (z-score) to predict rainfall (mm) \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & -0.06 & 0.41 \\ \textcolor{grey}{1} & 1.15 & -0.95 \\ \textcolor{grey}{1} & 0.18 & -0.68 \\ \textcolor{grey}{1} & -1.28 & 1.22 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 6 \\ 7 \\ 6 \\ 4 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 5.7 \\ 7.2 \\ 5.9 \\ 4.2 \\ \end{pmatrix}

\hat{y}(\boldsymbol{x}) = \beta_0 x_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_p x_p = \langle \boldsymbol{\beta}, \boldsymbol{x} \rangle

weather <- data.frame(temperature = c(27, 32, 28, 22), humidity = c(80, 70, 72, 86))
weather <- data.frame(scale(weather))
rainfall <- c(6, 7, 6, 4)
model <- lm(rainfall ~ temperature + humidity, data = weather)
summary(model)$coefficients

            Estimate Std. Error    t value   Pr(>|t|)
(Intercept) 5.750000  0.1961608 29.3126889 0.02170981
temperature 1.408455  0.6236204  2.2585129 0.26535876
humidity    0.185179  0.6236204  0.2969418 0.81624051

predict(model, newdata = weather)

       1        2        3        4 
5.739526 7.201275 5.881603 4.177596 

SLR with categorical inputs

Scenario: use property type to predict its sale price ($)

\boldsymbol{x} = \begin{pmatrix} \textcolor{red}{\text{Unit}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{blue}{\text{House}} \\ \end{pmatrix} \longrightarrow \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 1 & 0 \\ \textcolor{grey}{1} & 0 & 1 \\ \textcolor{grey}{1} & 0 & 1 \\ \textcolor{grey}{1} & 0 & 0 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 300000 \\ 500000 \\ 510000 \\ 700000 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 300000 \\ 505000 \\ 505000 \\ 700000 \\ \end{pmatrix}

\hat{y}(x) = \beta_0 + \beta_1 \underbrace{I(x = \textcolor{red}{\text{Unit}})}_{=: x_1} + \beta_2 \underbrace{I(x = \textcolor{green}{\text{TownHouse}})}_{=: x_2} = \beta_0 + \beta_1 x_1 + \beta_2 x_2

type <- factor(c("Unit", "TownHouse", "TownHouse", "House"))
price <- c(300000, 500000, 510000, 700000)
model <- lm(price ~ type)
summary(model)$coefficients

              Estimate Std. Error   t value    Pr(>|t|)
(Intercept)     700000   7071.068  98.99495 0.006430612
typeTownHouse  -195000   8660.254 -22.51666 0.028254710
typeUnit       -400000  10000.000 -40.00000 0.015912180

predict(model, newdata = data.frame(type))

     1      2      3      4 
300000 505000 505000 700000 

Changing the base case

Scenario: use property type to predict its sale price ($)

\boldsymbol{x} = \begin{pmatrix} \textcolor{red}{\text{Unit}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{blue}{\text{House}} \\ \end{pmatrix} \longrightarrow \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 0 & 0 \\ \textcolor{grey}{1} & 1 & 0 \\ \textcolor{grey}{1} & 1 & 0 \\ \textcolor{grey}{1} & 0 & 1 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 300000 \\ 500000 \\ 510000 \\ 700000 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 300000 \\ 505000 \\ 505000 \\ 700000 \\ \end{pmatrix}

\hat{y}(x) = \beta_0 + \beta_1 \underbrace{I(x = \textcolor{green}{\text{TownHouse}})}_{=: x_1} + \beta_2 \underbrace{I(x = \textcolor{blue}{\text{House}})}_{=: x_2} = \beta_0 + \beta_1 x_1 + \beta_2 x_2

type <- factor(c("Unit", "TownHouse", "TownHouse", "House"), levels = c("Unit", "TownHouse", "House"))
price <- c(300000, 500000, 510000, 700000)
model <- lm(price ~ type)
summary(model)$coefficients

              Estimate Std. Error  t value   Pr(>|t|)
(Intercept)     300000   7071.068 42.42641 0.01500249
typeTownHouse   205000   8660.254 23.67136 0.02687811
typeHouse       400000  10000.000 40.00000 0.01591218

predict(model, newdata = data.frame(type))

     1      2      3      4 
300000 505000 505000 700000 

Changing the target’s units

Scenario: use property type to predict its sale price ($000,000’s)

\boldsymbol{x} = \begin{pmatrix} \textcolor{red}{\text{Unit}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{green}{\text{TownHouse}} \\ \textcolor{blue}{\text{House}} \\ \end{pmatrix} \longrightarrow \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 0 & 0 \\ \textcolor{grey}{1} & 1 & 0 \\ \textcolor{grey}{1} & 1 & 0 \\ \textcolor{grey}{1} & 0 & 1 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 0.3 \\ 0.5 \\ 0.51 \\ 0.7 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} 0.3 \\ 0.505 \\ 0.505 \\ 0.7 \\ \end{pmatrix}

\hat{y}(x) = \beta_0 + \beta_1 \underbrace{I(x = \textcolor{green}{\text{TownHouse}})}_{=: x_1} + \beta_2 \underbrace{I(x = \textcolor{blue}{\text{House}})}_{=: x_2} = \beta_0 + \beta_1 x_1 + \beta_2 x_2

type <- factor(c("Unit", "TownHouse", "TownHouse", "House"), levels = c("Unit", "TownHouse", "House"))
price <- c(0.3, 0.5, 0.51, 0.7)
model <- lm(price ~ type)
summary(model)$coefficients

              Estimate  Std. Error  t value   Pr(>|t|)
(Intercept)      0.300 0.007071068 42.42641 0.01500249
typeTownHouse    0.205 0.008660254 23.67136 0.02687811
typeHouse        0.400 0.010000000 40.00000 0.01591218

predict(model, newdata = data.frame(type))

    1     2     3     4 
0.300 0.505 0.505 0.700 

Dates as categorical inputs

Imagine you had dataset with 157,209 rows and one covariate column was ‘date of birth’. There were 27,485 unique values for the date of birth column. You make a linear regression with the date of birth as an input, and treat it as a categorical variable (the default behaviour for text data in R).

R would make a design matrix of size 157,209 \times 27,485. This has 4,320,889,365 numbers in it. Each number is stored as 8 bytes, so the matrix is roughly 34,000,000,000 \text{ bytes} = 34,000,000 \text{ KB} = 34,000 \text{ MB} = 34 \text{ GB}.

Question: How do we avoid this situation of crashing our computer with an ‘out of memory’ error?

Solution: Don’t train on the date of birth — at least, not as a categorical variable. Turn it into a numerical variable, e.g. age. If the date column were not ‘date of birth’, maybe calculate the number of days since some reference date, or split into day, month, year columns.

Generalised Linear Models Recap

MLR with categorical targets

Scenario: use tumour radius (mm) and ages (years) to predict benign or malignant \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 14.8 & 48 \\ \textcolor{grey}{1} & 16.4 & 49 \\ \textcolor{grey}{1} & 15.5 & 47 \\ \textcolor{grey}{1} & 14.2 & 46 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} \text{Benign} \\ \text{Malignant} \\ \text{Benign} \\ \text{Malignant} \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} ? \\ ? \\ ? \\ ? \\ \end{pmatrix}

Step 1: Make a linear prediction \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p , \quad \text{a.k.a.} \quad \langle \boldsymbol{\beta}, \boldsymbol{x} \rangle.

Step 2: Shove it through some function to make it a probability \sigma(\langle \boldsymbol{\beta}, \boldsymbol{x} \rangle) Interpret that as being the probability of the positive class.

Step 3: Make a decision based on that probability. E.g., if the probability is greater than 0.5, predict the positive class.

Binomial regression

Scenario: use tumour radius (mm) and ages (years) to predict benign or malignant \boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 14.8 & 48 \\ \textcolor{grey}{1} & 16.4 & 49 \\ \textcolor{grey}{1} & 15.5 & 47 \\ \textcolor{grey}{1} & 14.2 & 46 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} \text{Benign} \\ \textbf{\text{Malignant}} \\ \text{Benign} \\ \textbf{\text{Malignant}} \\ \end{pmatrix}, \quad \boldsymbol{X} \boldsymbol{\beta} = \begin{pmatrix} -0.46 \\ 0.18 \\ 0.37 \\ -0.09 \\ \end{pmatrix}

df <- data.frame(radius = c(14.8, 16.4, 15.5, 14.2), age = c(48, 49, 47, 46))
tumour <- factor(c("Benign", "Malignant", "Benign", "Malignant"))
model <- glm(tumour ~ radius + age, data = df, family = binomial)

Step 1: Make a linear prediction

linear <- predict(model, newdata = df, type = "link")
linear

          1           2           3           4 
-0.46393923  0.18380161  0.36575186 -0.08928047 

X <- model.matrix(~ radius + age, data = df)
beta <- coef(model)
t(X %*% beta)

              1         2         3           4
[1,] -0.4639392 0.1838016 0.3657519 -0.08928047

Logistic regression and probit regression

# Plot the sigmoid function
sigmoid <- function(x) 1 / (1 + exp(-x))
x <- seq(-6, 6, 0.1)
y <- sigmoid(x)
df <- data.frame(x = x, y = y)
ggplot(df, aes(x = x, y = y)) +
  geom_line(linewidth = 1.5) +  # Thicker lines
  xlab("x") +
  ylab("y") +
  ggtitle("Sigmoid function") +
  theme(aspect.ratio = 1)  # Square aspect ratio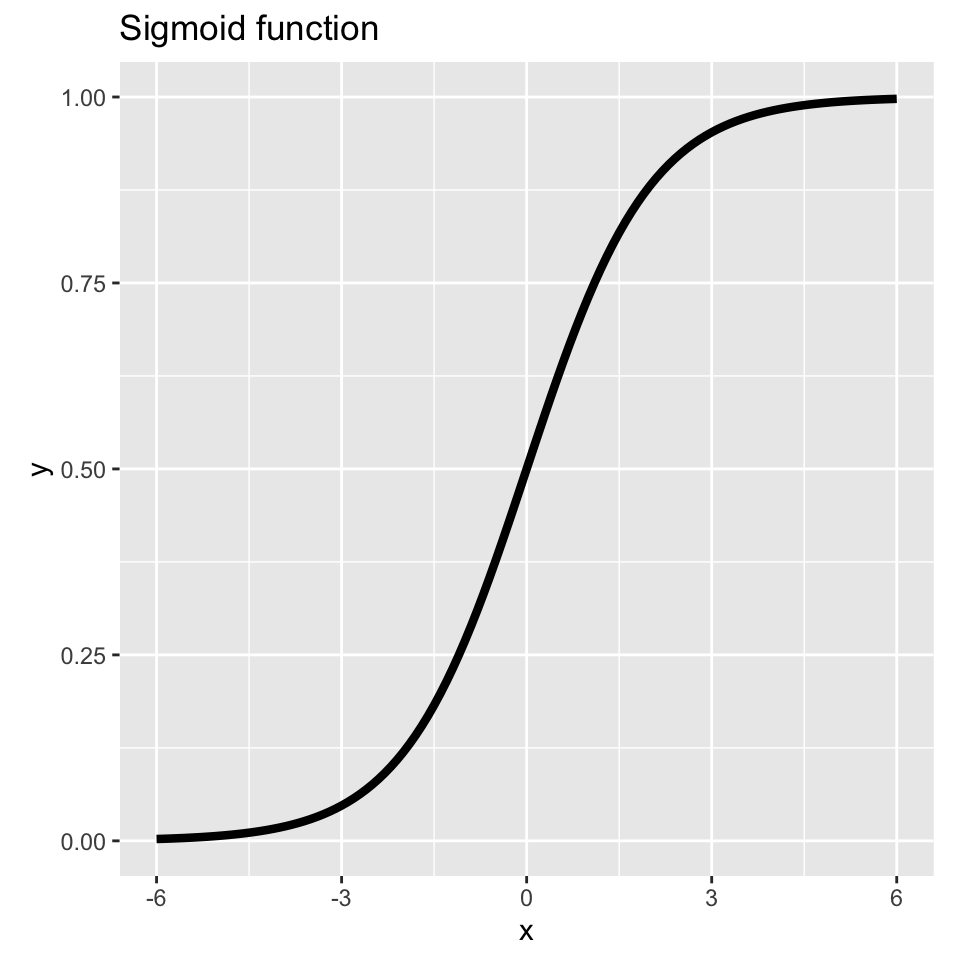

This give you logistic regression.

# Plot the Normal CDF function
x <- seq(-6, 6, 0.1)
y <- pnorm(x)
df <- data.frame(x = x, y = y)

ggplot(df, aes(x = x, y = y)) +
  geom_line(linewidth = 1.5) +  # Thicker lines
  xlab("x") +
  ylab("y") +
  ggtitle("Normal CDF function") +
  theme(aspect.ratio = 1)  # Square aspect ratio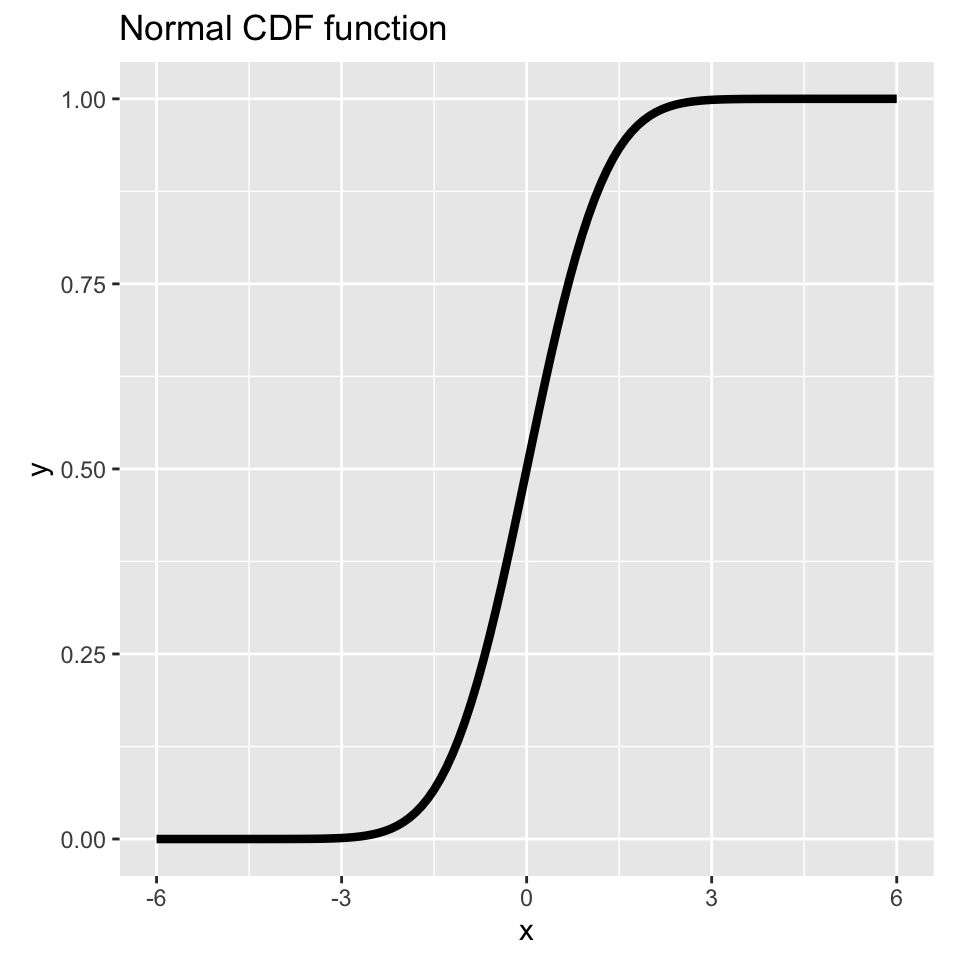

This gives you probit regression.

Logistic Regression

Scenario: use tumour radius (mm) and ages (years) to predict benign or malignant \boldsymbol{y} = \begin{pmatrix} \text{Benign} \\ \textbf{\text{Malignant}} \\ \text{Benign} \\ \textbf{\text{Malignant}} \\ \end{pmatrix}, \quad \boldsymbol{X} \boldsymbol{\beta} = \begin{pmatrix} -0.46 \\ 0.18 \\ 0.37 \\ -0.09 \\ \end{pmatrix}, \quad \sigma( \boldsymbol{X} \boldsymbol{\beta} ) = \begin{pmatrix} 39\% \\ 55\% \\ 59\% \\ 48\% \\ \end{pmatrix}

df <- data.frame(radius = c(14.8, 16.4, 15.5, 14.2), age = c(48, 49, 47, 46))
tumour <- factor(c("Benign", "Malignant", "Benign", "Malignant"))
model <- glm(tumour ~ radius + age, data = df, family = binomial)

Step 2: Shove it through some function to make it a probability

sigmoid <- function(x) 1 / (1 + exp(-x))
sigmoid(linear)

        1         2         3         4 
0.3860517 0.5458215 0.5904321 0.4776947 

predict(model, newdata = df, type = "response")

        1         2         3         4 
0.3860517 0.5458215 0.5904321 0.4776947 

Predicting categories

Scenario: use tumour radius (mm) and ages (years) to predict benign or malignant \boldsymbol{y} = \begin{pmatrix} \text{Benign} \\ \textbf{\text{Malignant}} \\ \text{Benign} \\ \textbf{\text{Malignant}} \\ \end{pmatrix}, \quad \sigma( \boldsymbol{X} \boldsymbol{\beta} ) = \begin{pmatrix} 39\% \\ 55\% \\ 59\% \\ 48\% \\ \end{pmatrix} , \quad \hat{\boldsymbol{y}} = \begin{pmatrix} \text{Benign} \\ \text{Malignant} \\ \text{Malignant} \\ \text{Benign} \\ \end{pmatrix}

df <- data.frame(radius = c(14.8, 16.4, 15.5, 14.2), age = c(48, 49, 47, 46))
tumour <- factor(c("Benign", "Malignant", "Benign", "Malignant"))
model <- glm(tumour ~ radius + age, data = df, family = binomial)

predict_probs <- predict(model, newdata = df, type = "response")
round(100 * predict_probs, 2)

    1     2     3     4 
38.61 54.58 59.04 47.77 

cutoff <- 0.5
predicted_tumours <- ifelse(predict_probs > cutoff, "Malignant", "Benign")
print(predicted_tumours)

          1           2           3           4 
   "Benign" "Malignant" "Malignant"    "Benign" 

Assessing accuracy in classification problems

Scenario: use tumour radius (mm) and ages (years) to predict benign or malignant \boldsymbol{y} = \begin{pmatrix} \textcolor{Green}{\text{Benign}} \\ \textcolor{Green}{\text{Malignant}} \\ \textcolor{Red}{\text{Benign}} \\ \textcolor{Red}{\text{Malignant}} \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} \textcolor{Green}{\text{Benign}} \\ \textcolor{Green}{\text{Malignant}} \\ \textcolor{Red}{\text{Malignant}} \\ \textcolor{Red}{\text{Benign}} \\ \end{pmatrix}

Accuracy: \frac{1}{n}\sum_{i=1}^n I(y_i = \hat{y}_i)

Error rate: \frac{1}{n}\sum_{i=1}^n I(y_i \neq \hat{y}_i)

Note

The word “accuracy” is used often used loosely when discussing models, particularly regression models. In the context of classification it has this specific meaning.

Poisson regression

Scenario: use population density to predict the daily count of gun violence incidents

\boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 10 \\ \textcolor{grey}{1} & 15 \\ \textcolor{grey}{1} & 12 \\ \textcolor{grey}{1} & 18 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 155 \\ 208 \\ 116 \\ 301 \\ \end{pmatrix}, \quad \hat{\boldsymbol{y}} = \begin{pmatrix} ? \\ ? \\ ? \\ ? \\ \end{pmatrix}

Step 1: Make a linear prediction \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p , \quad \text{a.k.a.} \quad \langle \boldsymbol{\beta}, \boldsymbol{x} \rangle.

Step 2: Shove it through some function to make it positive \exp(\langle \boldsymbol{\beta}, \boldsymbol{x} \rangle) Interpret that as being the expected count.

Predict the mean of a Poisson distribution

Scenario: use population density to predict the daily count of gun violence incidents

\boldsymbol{X} = \begin{pmatrix} \textcolor{grey}{1} & 10 \\ \textcolor{grey}{1} & 15 \\ \textcolor{grey}{1} & 12 \\ \textcolor{grey}{1} & 18 \\ \end{pmatrix}, \quad \boldsymbol{y} = \begin{pmatrix} 155 \\ 208 \\ 116 \\ 301 \\ \end{pmatrix}, \quad \boldsymbol{X} \boldsymbol{\beta} = \begin{pmatrix} 4.82 \\ 5.35 \\ 5.03 \\ 5.67 \\ \end{pmatrix}, \quad \hat{\boldsymbol{\mu}} = \begin{pmatrix} 125.1 \\ 211.3 \\ 154.3 \\ 289.4 \\ \end{pmatrix}

guns <- data.frame(density = c(10, 15, 12, 18))
incidents <- c(155, 208, 116, 301)
model <- glm(incidents ~ density, data = guns, family = poisson)
summary(model)$coefficients

             Estimate Std. Error   z value     Pr(>|z|)
(Intercept) 3.7803729 0.17881503 21.141248 3.321765e-99
density     0.1048546 0.01190339  8.808802 1.264908e-18

predict(model, newdata = guns, type = "link")

       1        2        3        4 
4.828919 5.353192 5.038628 5.667756 

predict(model, newdata = guns, type = "response")

       1        2        3        4 
125.0757 211.2817 154.2583 289.3844 

Splines (Week 8)

Trees (Week 9)

model <- rpart(tumour ~ radius + age, data = df, control = rpart.control(minsplit = 2))
rpart.plot(model)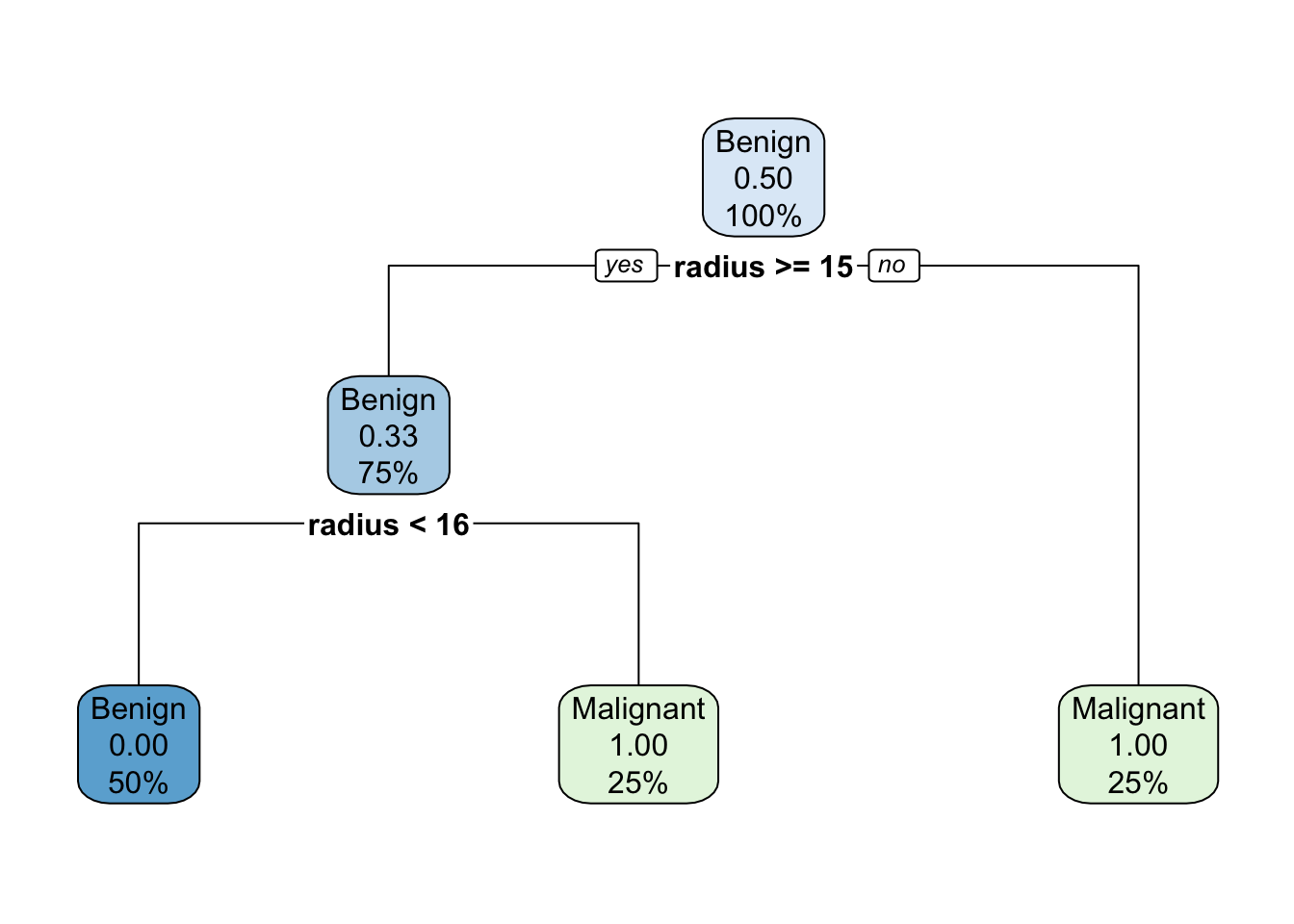

Glassdoor Dataset

Glassdoor Job Reviews

“This large dataset contains job descriptions and rankings among various criteria such as work-life balance, income, culture, etc. The data covers the various industries in the UK. Great dataset for multidimensional sentiment analysis.”

Original dataset is 300 MB, so I just took a subset of it. Focused on firms that have the word “University” in their name.

Dall-E 2 rendition of this dataset

Source: Kaggle, Glassdoor Job Reviews

The columns

Rankings are 1–5:

• overall_rating: rating for the job (target)
• work_life_balance: sub-rating: work-life balance
• culture_values: sub-rating: culture
• diversity_inclusion: sub-rating: diversity and inclusion
• career_opp: sub-rating: career opportunities
• comp_benefits: sub-rating: compensation and benefits
• senior_mgmt: sub-rating: senior management

Last two are coded: v - Positive, r - Mild, x - Negative, o - No opinion

• recommend: recommend the firm
• ceo_approv: approves firm’s CEO

Source: Kaggle, Glassdoor Job Reviews

Load the data

Available at https://laub.au/ml/data/uni_reviews.csv.

df_uni <- read.csv("uni_reviews.csv")
df_uni

# A tibble: 18,358 × 18
   firm  date_review job_title current location overall_rating work_life_balance
   <chr> <chr>       <chr>     <chr>   <chr>             <int>             <dbl>
 1 Birm… 2012-06-28  " Operat… Curren… "Birmin…              5                 4
 2 Birm… 2014-04-23  " Inform… Curren… "Birmin…              4                 5
 3 Birm… 2014-05-05  " "       Curren… ""                    4                 3
 4 Birm… 2014-07-18  " Out Re… Curren… "Birmin…              2                 5
 5 Birm… 2014-12-05  " Profes… Curren… "Birmin…              5                 5
 6 Birm… 2015-07-28  " Anonym… Curren… ""                    3                 2
 7 Birm… 2015-08-20  " Anonym… Former… ""                    4                 5
 8 Birm… 2015-11-05  " Studen… Curren… "Birmin…              5                 5
 9 Birm… 2015-11-19  " Senior… Curren… ""                    3                 3
10 Birm… 2016-01-04  " Operat… Former… "Birmin…              4                 5
# ℹ 18,348 more rows
# ℹ 11 more variables: culture_values <dbl>, diversity_inclusion <dbl>,
#   career_opp <dbl>, comp_benefits <dbl>, senior_mgmt <dbl>, recommend <chr>,
#   ceo_approv <chr>, outlook <chr>, headline <chr>, pros <chr>, cons <chr>

Bird’s eye view of the data

summary(df_uni)

     firm           date_review         job_title           current         
 Length:18358       Length:18358       Length:18358       Length:18358      
 Class :character   Class :character   Class :character   Class :character  
 Mode  :character   Mode  :character   Mode  :character   Mode  :character  
                                                                            
                                                                            
                                                                            
                                                                            
   location         overall_rating  work_life_balance culture_values 
 Length:18358       Min.   :1.000   Min.   :1.00      Min.   :1.000  
 Class :character   1st Qu.:4.000   1st Qu.:3.00      1st Qu.:3.000  
 Mode  :character   Median :4.000   Median :4.00      Median :4.000  
                    Mean   :4.136   Mean   :3.89      Mean   :3.962  
                    3rd Qu.:5.000   3rd Qu.:5.00      3rd Qu.:5.000  
                    Max.   :5.000   Max.   :5.00      Max.   :5.000  
                                    NA's   :5316      NA's   :5782   
 diversity_inclusion   career_opp    comp_benefits    senior_mgmt   
 Min.   :1.000       Min.   :1.000   Min.   :1.000   Min.   :1.000  
 1st Qu.:4.000       1st Qu.:3.000   1st Qu.:3.000   1st Qu.:3.000  
 Median :5.000       Median :4.000   Median :4.000   Median :4.000  
 Mean   :4.146       Mean   :3.649   Mean   :3.542   Mean   :3.484  
 3rd Qu.:5.000       3rd Qu.:5.000   3rd Qu.:5.000   3rd Qu.:5.000  
 Max.   :5.000       Max.   :5.000   Max.   :5.000   Max.   :5.000  
 NA's   :15448       NA's   :5226    NA's   :5452    NA's   :5641   
  recommend          ceo_approv          outlook            headline        
 Length:18358       Length:18358       Length:18358       Length:18358      
 Class :character   Class :character   Class :character   Class :character  
 Mode  :character   Mode  :character   Mode  :character   Mode  :character  
                                                                            
                                                                            
                                                                            
                                                                            
     pros               cons          
 Length:18358       Length:18358      
 Class :character   Class :character  
 Mode  :character   Mode  :character  
                                      
                                      
                                      
                                      

Look for common jobs and universities

table(df_uni$firm) %>% sort(decreasing = TRUE) %>% head(10)

   University-of-Michigan University-College-London         Oxford-University 
                     4185                      1259                      1238 
  University-of-Cambridge  University-of-Manchester   University-of-Edinburgh 
                     1199                       861                       682 
 University-of-Nottingham     University-of-Warwick       University-of-Leeds 
                      678                       590                       548 
  University-of-Sheffield 
                      518 

table(df_uni$job_title) %>% sort(decreasing = TRUE) %>% head(10)

              Anonymous Employee                                  
                            3817                             1581 
                         Student                      PhD Student 
                             992                              940 
              Research Assistant               Research Associate 
                             592                              577 
 Postdoctoral Research Associate               Student Ambassador 
                             325                              317 
                        Lecturer                  Research Fellow 
                             262                              216 

Look at the textual data

# Print a random sample of 'pros' and 'cons'
set.seed(123)
sample(df_uni$pros, 5)

[1] "Good Staff and Work Environment, Cheap cost of living."                                                                                                                                                                                                                          
[2] "Amazing people, depts vary. Some research groups are disfunctional, some are amazing places. The one I am is amazing."                                                                                                                                                           
[3] "Amazing University. As well as working within the area I was assigned it was encouraged that interns seek out people from other parts of the company in order to learn more about the different areas within RR.\n- Supportive Team\n- Loads of Feedback\n- Interesting Projects"
[4] "It was a great learning experience among many experienced professionals in the health care industry."                                                                                                                                                                            
[5] "Great city, great campus, good relationships between academic and administrative/technical staff, strong NSS results and a desire to maintain the student experience and grow the high quality research output."                                                                 

sample(df_uni$cons, 5)

[1] "poor management and divide and rule tactics have driven most staff to leave their jobs"                                               
[2] "Not much work to do which result in limited experience."                                                                              
[3] "Not enough pay for the work you do in certain departments"                                                                            
[4] "long job hours sometimes go past 40hrs a week"                                                                                        
[5] "Bureaucratic. There are support mechanisms but sometimes, needs lots of approval. IT is also slow. Needs better balance in workloads."

Change some bizarre coding scheme

Two columns had: v - Positive, r - Mild, x - Negative, o - No opinion

table(df_uni$recommend)

   o    v    x 
7458 9202 1698 

table(df_uni$ceo_approv)

   o    r    v    x 
9869 3646 4042  801 

df_uni <- df_uni %>%
  mutate(
    recommend = factor(recode(recommend, 
                              "v" = "Positive", 
                              "r" = "Mild", 
                              "x" = "Negative", 
                              "o" = "No opinion"), 
                       levels = c("No opinion", "Positive", "Mild", "Negative")),
    ceo_approv = factor(recode(ceo_approv, 
                               "v" = "Positive", 
                               "r" = "Mild", 
                               "x" = "Negative", 
                               "o" = "No opinion"), 
                        levels = c("No opinion", "Positive", "Mild", "Negative"))
  )

table(df_uni$recommend)

No opinion   Positive       Mild   Negative 
      7458       9202          0       1698 

table(df_uni$ceo_approv)

No opinion   Positive       Mild   Negative 
      9869       4042       3646        801 

Removing missing values

df_uni <- df_uni[complete.cases(df_uni[, c("work_life_balance", "culture_values", "career_opp",
        "comp_benefits", "senior_mgmt", "overall_rating", "recommend", "ceo_approv")]), ]
df_uni

# A tibble: 12,124 × 18
   firm  date_review job_title current location overall_rating work_life_balance
   <chr> <chr>       <chr>     <chr>   <chr>             <int>             <dbl>
 1 Birm… 2012-06-28  " Operat… Curren… "Birmin…              5                 4
 2 Birm… 2014-04-23  " Inform… Curren… "Birmin…              4                 5
 3 Birm… 2014-05-05  " "       Curren… ""                    4                 3
 4 Birm… 2014-07-18  " Out Re… Curren… "Birmin…              2                 5
 5 Birm… 2014-12-05  " Profes… Curren… "Birmin…              5                 5
 6 Birm… 2015-07-28  " Anonym… Curren… ""                    3                 2
 7 Birm… 2015-08-20  " Anonym… Former… ""                    4                 5
 8 Birm… 2015-11-05  " Studen… Curren… "Birmin…              5                 5
 9 Birm… 2015-11-19  " Senior… Curren… ""                    3                 3
10 Birm… 2016-01-04  " Operat… Former… "Birmin…              4                 5
# ℹ 12,114 more rows
# ℹ 11 more variables: culture_values <dbl>, diversity_inclusion <dbl>,
#   career_opp <dbl>, comp_benefits <dbl>, senior_mgmt <dbl>, recommend <fct>,
#   ceo_approv <fct>, outlook <chr>, headline <chr>, pros <chr>, cons <chr>

Make a model

Regress over the sub-rankings

model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values +
        career_opp + comp_benefits + senior_mgmt, data = df_uni)
summary(model_subrankings)

Call:
lm(formula = overall_rating ~ work_life_balance + culture_values + 
    career_opp + comp_benefits + senior_mgmt, data = df_uni)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.1733 -0.2923 -0.0585  0.3605  3.3510 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       0.767970   0.022694   33.84   <2e-16 ***
work_life_balance 0.087806   0.005854   15.00   <2e-16 ***
culture_values    0.305204   0.007081   43.10   <2e-16 ***
career_opp        0.208360   0.005867   35.52   <2e-16 ***
comp_benefits     0.071375   0.005619   12.70   <2e-16 ***
senior_mgmt       0.208329   0.006618   31.48   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5906 on 12118 degrees of freedom
Multiple R-squared:  0.6873,    Adjusted R-squared:  0.6872 
F-statistic:  5327 on 5 and 12118 DF,  p-value: < 2.2e-16

Make another model

Regress over the recommend and ceo_approv

model_recommend <- lm(overall_rating ~ recommend + ceo_approv, data = df_uni)
summary(model_recommend)

Call:
lm(formula = overall_rating ~ recommend + ceo_approv, data = df_uni)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.5708 -0.5220 -0.0557  0.5978  3.0196 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         4.05573    0.01583 256.264  < 2e-16 ***
recommendPositive   0.34650    0.02180  15.894  < 2e-16 ***
recommendNegative  -1.53373    0.02916 -52.589  < 2e-16 ***
ceo_approvPositive  0.16852    0.02062   8.173 3.31e-16 ***
ceo_approvMild     -0.18989    0.02065  -9.196  < 2e-16 ***
ceo_approvNegative -0.54163    0.03505 -15.454  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7865 on 12118 degrees of freedom
Multiple R-squared:  0.4454,    Adjusted R-squared:  0.4452 
F-statistic:  1947 on 5 and 12118 DF,  p-value: < 2.2e-16

Statistical Model Evaluation

Model evaluation

You fit a few models, then ask:

1. Model Selection: Which of these models is the best?
2. Future Performance: How good should we expect the final model to be on unseen data?

If we make a claim about a model’s performance, we prefer to be pessimistic (underestimate) rather than optimistic (overestimate).

Note

Question: Say, I fit a few models by minimising the training error (MSE).

Then I pick the model with the lowest MSE as my favourite model.

Lastly, I predict that for future data, it will have a similar MSE.

What can go wrong?

Overfitting I

Overfitting II

Overfitting III

The ‘statistical’ or ‘indirect’ approach

Bragging about a good RSS is like saying “I can predict with 100% accuracy what I had for lunch yesterday”.

Combine RSS with a penalty for the complexity of the model (p predictors):

C_p = \frac{1}{n}(\text{RSS} + 2p \hat{\sigma}^2) \text{AIC} = \frac{1}{n}(\text{RSS} + 2p \hat{\sigma}^2) \text{BIC} = \frac{1}{n}(\text{RSS}+\log(n) \, p\hat{\sigma}^2) \text{Adjusted } R^2 = 1-\frac{\text{RSS}/(n-p-1)}{\text{TSS}/(n-1)}

Note

These definitions are from the textbook, but they’re not actually correct (they’ve been simplified).

For the Glassdoor models

Model 1

AIC(model_subrankings)

[1] 21646.59

BIC(model_subrankings)

[1] 21698.41

summary(model_subrankings)$adj.r.squared

[1] 0.6871576

Model 2

AIC(model_recommend)

[1] 28592.3

BIC(model_recommend)

[1] 28644.12

summary(model_recommend)$adj.r.squared

[1] 0.4452108

Which is the better model (according to this ‘indirect’ approach)?

Validation Set Approach

The ML approach

Just make predictions on new data

Set aside a fraction after shuffling.

Illustration of a typical training/test split.

Note

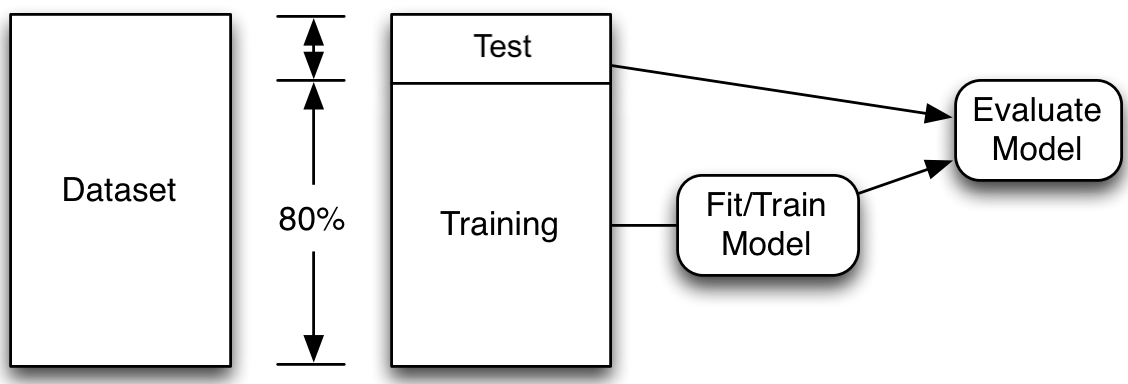
The model’s metrics on the test set are the test set error. Note, there is also the term test error which is the model’s error on unseen data. So, test set error is an estimate of the test error.

Adapted from: Heaton (2022), Applications of Deep Learning, Part 2.1: Introduction to Pandas.

The validation set approach

Splitting the data.

1. For each model, fit it to the training set.
2. Compute the error for each model on the validation set.
3. Select the model with the lowest validation error.
4. Compute the error of the final model on the test set.

Source: Wikipedia.

Getting random rows

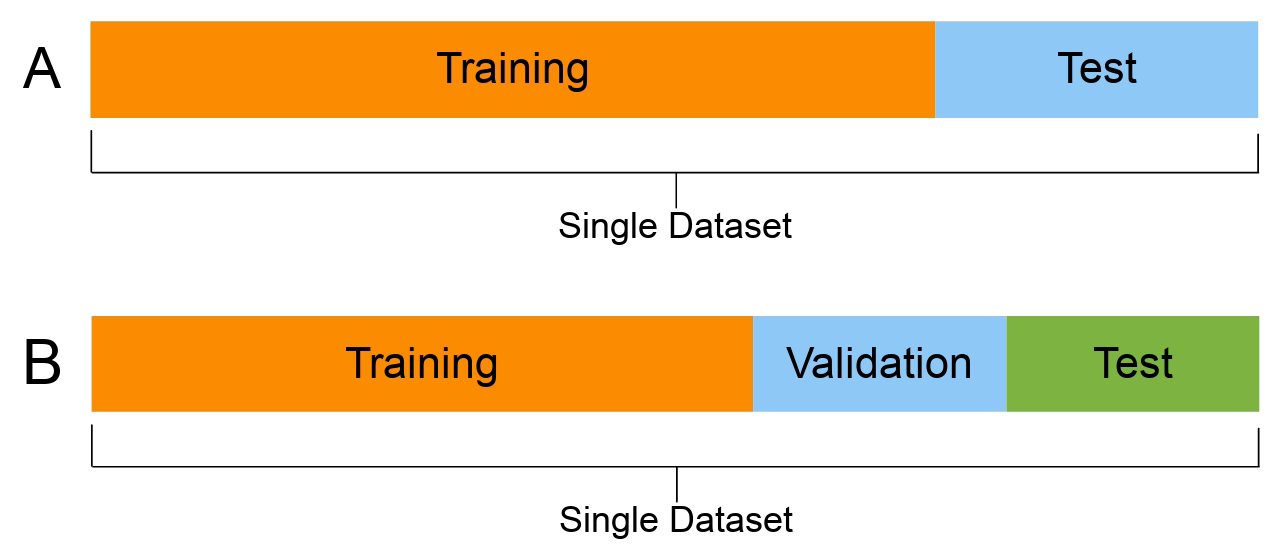
df_toy <- data.frame(thing = c("croissant", "coffee", "gadgets", "books", "music"),
                     cost = c(9, 5, 100, 20, 40))

Using the sample function:

set.seed(42)
sample(df_toy$thing, 3)

[1] "croissant" "music"     "books"    

You can use 1:nrow(df_toy) to get all the possible indices of the data frame.

three_indices <- sample(1:nrow(df_toy), 3)
three_indices

[1] 1 2 4

df_toy[three_indices, ]

# A tibble: 3 × 2
  thing      cost
  <chr>     <dbl>
1 croissant     9
2 coffee        5
3 books        20

df_toy[-three_indices, ]

# A tibble: 2 × 2
  thing    cost
  <chr>   <dbl>
1 gadgets   100
2 music      40

Split the data

First extract the test dataset:

set.seed(123)
test_index <- sample(1:nrow(df_uni), 0.2 * nrow(df_uni))
test <- df_uni[test_index, ]
train_val <- df_uni[-test_index, ]

Then split the rest into validation and test sets:

val_index <- sample(1:nrow(train_val), 0.25 * nrow(train_val))
val <- train_val[val_index, ]
train <- train_val[-val_index, ]

dim(train)

[1] 7275   18

dim(val)

[1] 2425   18

dim(test)

[1] 2424   18

Remember, models tend to be improve with more data (not always!).

Train on train, compare on val, test on test

Train on training set:

model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values +
        career_opp + comp_benefits + senior_mgmt, data = train)
model_recommend <- lm(overall_rating ~ recommend + ceo_approv, data = train)

Pick the model with the lowest validation error:

val_pred_subrankings <- predict(model_subrankings, newdata = val)
mean((val_pred_subrankings - val$overall_rating)^2)

[1] 0.3484431

val_pred_recommend <- predict(model_recommend, newdata = val)
mean((val_pred_recommend - val$overall_rating)^2)

[1] 0.6313695

Take only the selected model, and calculate the test set error:

test_pred_subrankings <- predict(model_subrankings, newdata = test)
mean((test_pred_subrankings - test$overall_rating)^2)

[1] 0.346846

Expect training set error < validation set error < test set error (but not always!).

Why shuffle the data?

Let’s create a toy dataset where the target values are separated.

# Create a toy dataset
df_toy_classification <- data.frame(
  feature1 = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10),
  feature2 = c(2.5, 3.0, 3.9, 5.1, 6.6, 7.0, 7.5, 9.2, 10.4, 11.1),
  target = c(0, 0, 0, 0, 0, 0, 1, 1, 1, 1)
)

train_toy <- df_toy_classification[1:6, ]
test_toy <- df_toy_classification[7:10, ]

train_toy

# A tibble: 6 × 3
  feature1 feature2 target
     <dbl>    <dbl>  <dbl>
1        1      2.5      0
2        2      3        0
3        3      3.9      0
4        4      5.1      0
5        5      6.6      0
6        6      7        0

test_toy

# A tibble: 4 × 3
  feature1 feature2 target
     <dbl>    <dbl>  <dbl>
1        7      7.5      1
2        8      9.2      1
3        9     10.4      1
4       10     11.1      1

model <- glm(target ~ ., data = train_toy, family = binomial)
coef(model)

  (Intercept)      feature1      feature2 
-2.456607e+01 -1.638022e-14  1.377780e-14 

predict(model, newdata = test_toy, type = "response")

           7            8            9           10 
2.143345e-11 2.143345e-11 2.143345e-11 2.143345e-11 

Why not use validation set for both?

Thought experiment: have m classifiers: f_1(\boldsymbol{x}), \dots, f_m(\boldsymbol{x}).

They are just as good as each other in the long run \mathbb{P}(\, f_i(\boldsymbol{X}) = Y \,)\ =\ 90\% , \quad \text{for } i=1,\dots,m .

Evaluate each model on the validation set, some will be better than others.

If you just took the best, you’d think it has \approx 98\% accuracy!

set.seed(2)
m <- 50
x <- rnorm(m, mean = 0.9, sd = 0.03)
data <- data.frame(x = x, y = rep(0, m))

# Combined plot with histogram
p <- ggplot(data, aes(x = x)) +
  geom_histogram(aes(y = after_stat(density)), binwidth = 0.02, fill = "blue", alpha = 0.5, color = "black") +
  geom_point(aes(y = y)) +
  geom_vline(xintercept = 0.9, linetype = "dashed", color = "black") +
  geom_vline(xintercept = max(x), linetype = "dashed", color = "red") +
  labs(x = "Accuracy of each model on validation set", y = "Count") +
  xlim(min(x) - 0.02, max(x) + 0.02) +
  theme_minimal()

print(p)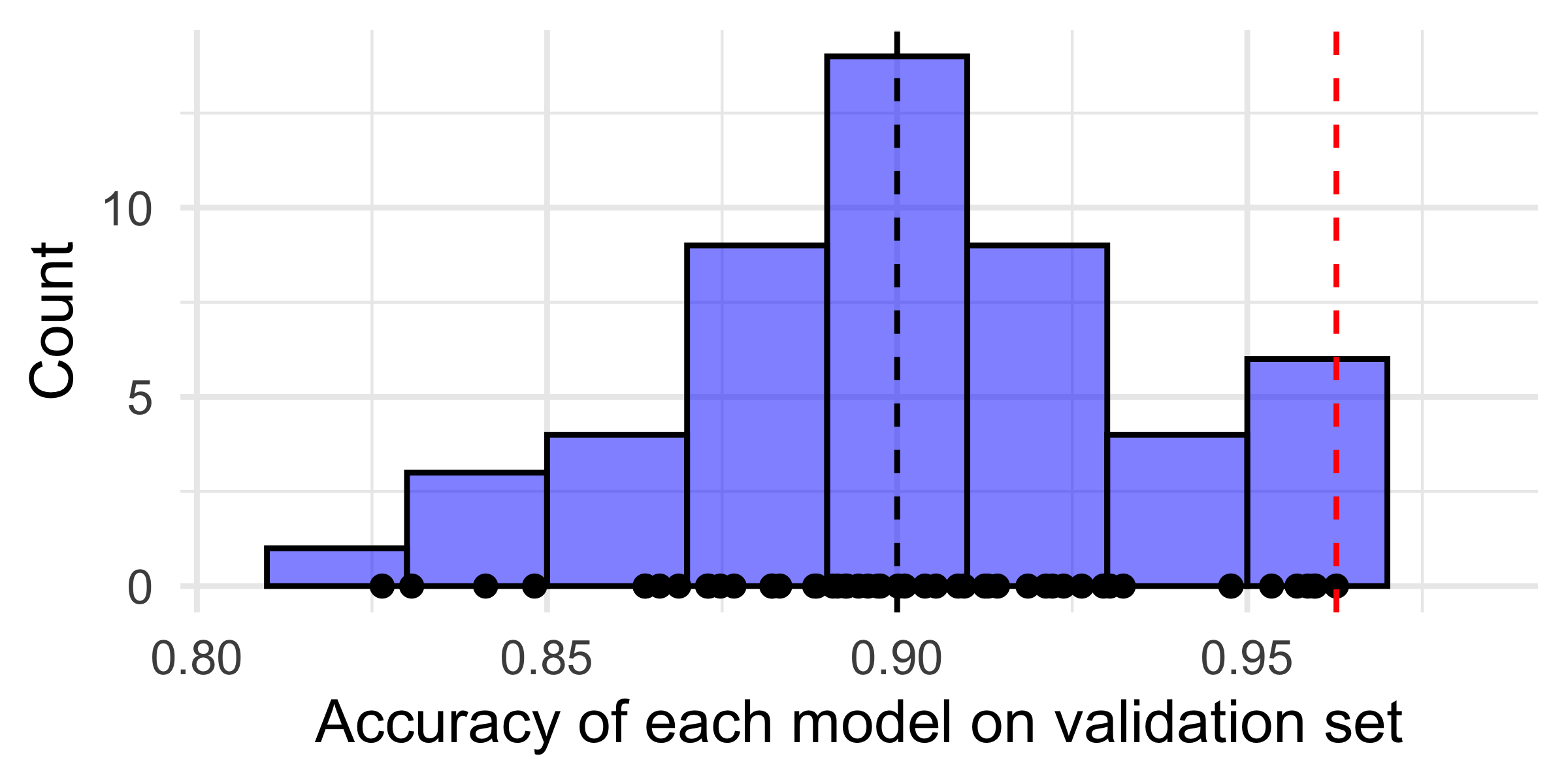

You get unbiased estimates for each model’s accuracy.

However, you get a biased estimate for the best model’s future performance.

Optionally, you can retrain once or twice

Your best validation set model only trained on a fraction (e.g. 60%) of the data.

Retrain on the train and validation set combined (often 80%):

model_subrankings_train_val <- update(model_subrankings, data = rbind(train, val))

Can still estimate the test error for this new model:

test_pred_subrankings_train_val <- predict(model_subrankings_train_val, newdata = test)
mean((test_pred_subrankings_train_val - test$overall_rating)^2)

[1] 0.3471235

Warning

Lastly, if you want the best possible model, you can retrain on the entire dataset:

model_subrankings_all <- update(model_subrankings, data = df_uni)

But we have no unseen data to test this on!

In theory, some outlier in the test set could make this model worse than the previous one.

Validation Set Approach

“In statistics, sometimes we only use a single data set. To still be able to evaluate the performance of the developed prediction model on the same data, sophisticated methods have developed over a long period of time and are still in use in some parts of the statistics community. These methods account for the fact that the model saw the data during fitting and applied corrections to account for that. These methods include, for example, the Akaike Information Criterion (AIC) or the Bayesian Information Criterion (BIC). Don’t get confused. If you have a validation set, you don’t need these methods.”

Source: Sic & Duerr (2020), Probabilistic Deep Learning, Chapter 5.

k-Fold Cross-Validation

Illustration

Illustration of 5-fold cross-validation.

Idea

• Randomly divided the set of observations into K groups, or folds of about equal size
  • the k^\text{th} fold is treated as a validation set
  • the remaining K-1 folds make up the training set
• Repeat K times resulting K estimates of the test error \mathrm{CV}_{(K)} = \frac{1}{K} \sum_{k=1}^{K} \mathrm{MSE}_k
• In practice K = 5 or K = 10
• LOOCV is a special case where K = n

Simulated Examples

Cross-Validation

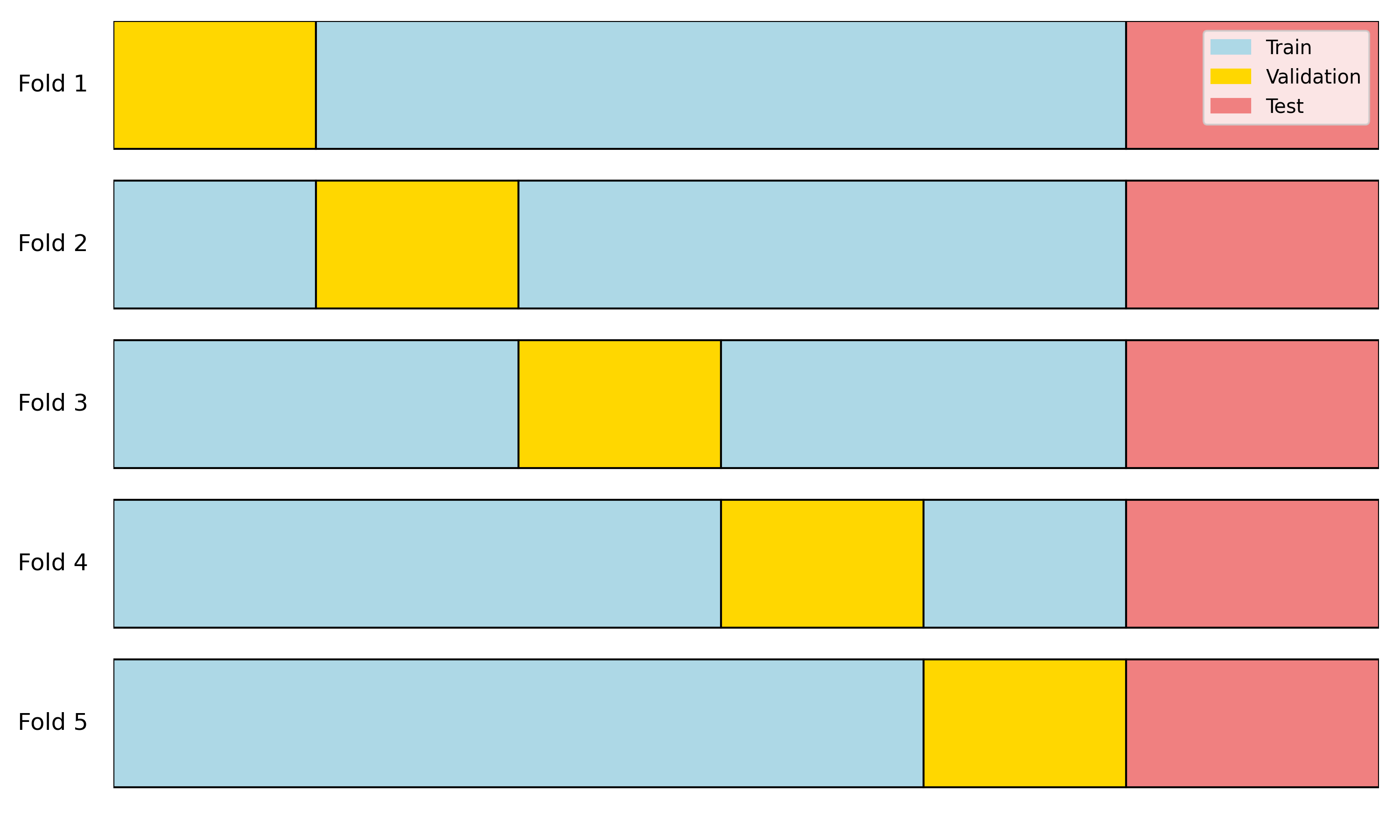
set.seed(123)
train_val <- rbind(train, val)
train_val_shuffle <- train_val[sample(1:nrow(train_val)), ]

k <- 5
fold_size <- floor(nrow(train_val) / k)
mse_subrankings <- numeric(k)
mse_recommend <- numeric(k)

for (i in 1:k) {
  val_indices <- ((i - 1) * fold_size + 1):(i * fold_size)
  val <- train_val_shuffle[val_indices, ]
  train <- train_val_shuffle[-val_indices, ]
  
  model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values +
                            career_opp + comp_benefits + senior_mgmt, data = train)
  model_recommend <- lm(overall_rating ~ recommend + ceo_approv, data = train)
  
  mse_subrankings[i] <- mean((predict(model_subrankings, newdata = val) - val$overall_rating)^2)
  mse_recommend[i] <- mean((predict(model_recommend, newdata = val) - val$overall_rating)^2)
}
mse_subrankings

[1] 0.3084817 0.3520156 0.3816378 0.3468752 0.3592670

mse_recommend

[1] 0.6047533 0.6084730 0.6381717 0.6427707 0.6503017

c(mean(mse_subrankings), mean(mse_recommend))

[1] 0.3496555 0.6288941

A linear model is a (Gaussian) GLM

model_recommend <- lm(
    overall_rating ~ recommend + ceo_approv,
    data = train_val)
summary(model_recommend)

Call:
lm(formula = overall_rating ~ recommend + ceo_approv, data = train_val)

Residuals:
    Min      1Q  Median      3Q     Max 
-3.5616 -0.5616 -0.0527  0.6026  3.0055 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         4.05265    0.01787 226.808  < 2e-16 ***
recommendPositive   0.34473    0.02456  14.036  < 2e-16 ***
recommendNegative  -1.52585    0.03269 -46.682  < 2e-16 ***
ceo_approvPositive  0.16426    0.02323   7.071 1.64e-12 ***
ceo_approvMild     -0.18919    0.02323  -8.145 4.25e-16 ***
ceo_approvNegative -0.53227    0.03941 -13.506  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7925 on 9694 degrees of freedom
Multiple R-squared:  0.4404,    Adjusted R-squared:  0.4401 
F-statistic:  1526 on 5 and 9694 DF,  p-value: < 2.2e-16

model_recommend <- glm(
    overall_rating ~ recommend + ceo_approv,
    data = train_val)
summary(model_recommend)

Call:
glm(formula = overall_rating ~ recommend + ceo_approv, data = train_val)

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         4.05265    0.01787 226.808  < 2e-16 ***
recommendPositive   0.34473    0.02456  14.036  < 2e-16 ***
recommendNegative  -1.52585    0.03269 -46.682  < 2e-16 ***
ceo_approvPositive  0.16426    0.02323   7.071 1.64e-12 ***
ceo_approvMild     -0.18919    0.02323  -8.145 4.25e-16 ***
ceo_approvNegative -0.53227    0.03941 -13.506  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for gaussian family taken to be 0.628)

    Null deviance: 10879.1  on 9699  degrees of freedom
Residual deviance:  6087.8  on 9694  degrees of freedom
AIC: 23023

Number of Fisher Scoring iterations: 2

Using cv.glm

Typically wouldn’t write your own loop, but use a function like cv.glm:

library(boot)

set.seed(123)

# Fit the models as 'glm's first
model_subrankings <- glm(overall_rating ~ work_life_balance + culture_values + career_opp +
    comp_benefits + senior_mgmt, data = train_val)
model_recommend <- glm(overall_rating ~ recommend + ceo_approv, data = train_val)

# Pass them to 'cv.glm'
cv_subrankings <- cv.glm(train_val, model_subrankings, K = 10)
cv_recommend <- cv.glm(train_val, model_recommend, K = 10)

(cv_mse_subrankings <- cv_subrankings$delta[1])

[1] 0.3496653

(cv_mse_recommend <- cv_recommend$delta[1])

[1] 0.6287906

Leave-One-Out Cross-Validation

LOOCV: Idea

• Split the set of observations into two parts:
  • a single observation (x_i, y_i) for the validation set
  • the remaining observations make up the training set: \{(x_1, y_1), \ldots, (x_{i-1}, y_{i-1}), (x_{i+1}, y_{i+1}), \ldots, (x_{n}, y_{n})\}
• Fit the model on the n-1 training observations
• Predict \hat{y}_i for the validation set
  • \mathrm{MSE}_i = (y_i - \hat{y}_i)^2 provides an approximately unbiased estimate for the test error
• Repeat the procedure n times
• The resulting LOOCV estimate for the test error is: \mathrm{CV}_{(n)} = \frac{1}{n} \sum_{i=1}^{n} \mathrm{MSE}_i

Validation set vs LOOCV - Discussion

Discuss how LOOCV performs relative to the Validation set approach - focusing in particular on the drawbacks of the Validation set approach identified previously.

LOOCV for least square linear models

• For linear (or polynomial) regression, LOOCV is extremely cheap to compute: \text{CV}_{(n)} = \frac{1}{n} \sum_{i=1}^n \left(\frac{y_i-\hat{y}_i}{1-h_i}\right)^2
• where
  • \hat{y}_i is the original least squares fit
  • h_i is the leverage defined in Chapter 3 (M2)
• This simplification generally does not apply in general

Note

LOOCV and this simplification is cute & historically important, but less practically so.

Harry Potter dataset

(movies <- read.csv("Movies.csv"))

# A tibble: 8 × 6
  Movie.ID Movie.Title                    Release.Year Runtime Budget Box.Office
     <int> <chr>                                 <int>   <int> <chr>  <chr>     
1        1 Harry Potter and the Philosop…         2001     152 "$125… "$1,002,0…
2        2 Harry Potter and the Chamber …         2002     161 "$100… "$880,300…
3        3 Harry Potter and the Prisoner…         2004     142 "$130… "$796,700…
4        4 Harry Potter and the Goblet o…         2005     157 "$150… "$896,400…
5        5 Harry Potter and the Order of…         2007     138 "$150… "$942,000…
6        6 Harry Potter and the Half-Blo…         2009     153 "$250… "$943,200…
7        7 Harry Potter and the Deathly …         2010     146 "$200… "$976,900…
8        8 Harry Potter and the Deathly …         2011     130 "$250… "$1,342,0…

# Clean the dataset and convert relevant columns to numerical format
movies$Budget <- as.numeric(gsub("[\\$,]", "", movies$Budget))
movies$Box.Office <- as.numeric(gsub("[\\$,]", "", movies$Box.Office))

# Grab just one movie as a test set
test_index <- sample(1:nrow(movies), 1)
train_val <- movies[-test_index, ]
(test <- movies[test_index, ])

# A tibble: 1 × 6
  Movie.ID Movie.Title                    Release.Year Runtime Budget Box.Office
     <int> <chr>                                 <int>   <int>  <dbl>      <dbl>
1        4 Harry Potter and the Goblet o…         2005     157  1.5e8  896400000

LOOCV for the Harry Potter dataset

model_year <- glm(Box.Office ~ Budget + Release.Year, data = train_val)
model_runtime <- glm(Box.Office ~ Budget + Runtime, data = train_val)

cv_year <- cv.glm(train_val, model_year) # cv.glm defaults to LOOCV
cv_runtime <- cv.glm(train_val, model_runtime)

cv_year$delta[1]

[1] 6.153881e+16

cv_runtime$delta[1]

[1] 5.905452e+16

# Test error for the runtime model
test_pred_runtime <- predict(model_runtime, newdata = test)
(mean((test_pred_runtime - test$Box.Office)^2))

[1] 1.575889e+14

summary(model_runtime)$coefficients

                 Estimate   Std. Error   t value  Pr(>|t|)
(Intercept)  1.708822e+09 1.040374e+09  1.642508 0.1758294
Budget       1.275637e+00 1.089689e+00  1.170643 0.3067254
Runtime     -6.473381e+06 6.444243e+06 -1.004522 0.3719641

Exam question 2023

# Load dataset
library(mlbench)
data(BostonHousing)

# Split the data into training and test sets
set.seed(123)
train_index <- sample(nrow(BostonHousing),
    0.8 * nrow(BostonHousing))
train <- BostonHousing[train_index, ]
test <- BostonHousing[-train_index, ]

# Fit a linear regression model
lm_model <- lm(medv ~ ., data = train)

# Calculate the training and test errors
train_pred <- predict(lm_model, newdata = train)
train_error <- mean((train_pred - train$medv)^2)
lm_model <- lm(medv ~ ., data = test)
test_pred <- predict(lm_model, newdata = test)
test_error <- mean((test_pred - test$medv)^2)

# Print the training and test errors
cat("Training Error (MSE):", train_error, "\n")

Training Error (MSE): 21.60875 

cat("Test Error (MSE):", test_error, "\n")

Test Error (MSE): 20.26994 

3a) Which do you expect to be lower on average, the training loss or the test loss? Why?

3b) Describe why, in this case, the test error is less than the training error.

Data leakage!

Regularisation

Tall data vs wide data

A tall dataset (n \gg p)

Traditional linear regression methods

A wide dataset (p \gg n)

Traditional methods break, regularisation methods can help

LMs with p > n

If p > n, R will just fit the first n parameters and give NA for the rest.

first_few_rows <- df_uni[1:3, ]
model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values +
        career_opp + comp_benefits + senior_mgmt, data = first_few_rows)
summary(model_subrankings)

Call:
lm(formula = overall_rating ~ work_life_balance + culture_values + 
    career_opp + comp_benefits + senior_mgmt, data = first_few_rows)

Residuals:
ALL 3 residuals are 0: no residual degrees of freedom!

Coefficients: (3 not defined because of singularities)
                  Estimate Std. Error t value Pr(>|t|)
(Intercept)         3.6667        NaN     NaN      NaN
work_life_balance  -0.3333        NaN     NaN      NaN
culture_values      0.6667        NaN     NaN      NaN
career_opp              NA         NA      NA       NA
comp_benefits           NA         NA      NA       NA
senior_mgmt             NA         NA      NA       NA

Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:    NaN 
F-statistic:   NaN on 2 and 0 DF,  p-value: NA

Shrinkage methods

• Alternative to subset selection is to fit model using all p predictors, but constraints, or regularizes the coefficients (=‘shrinks’ the coefficients)
• Two main types:
  • Ridge regression: pushes estimates towards zero, but all predictors included
  • Lasso regression: pushes estimates towards zero, some predictors excluded
  • (There’s also the elastic net, a which is a combination of ridge and lasso)
• Allows us to fit models with n < p

Ridge regression

Minimise on \beta:

\sum_{i=1}^n \Bigl( y_i - \beta_0 - \sum_{j=1}^p \beta_jx_{ij} \Bigr)^2 + \lambda \sum_{j=1}^p \beta^2_j = \text{RSS} + \lambda \sum_{j=1}^p \beta^2_j

• The shrinkage penalty \lambda\sum_{j=1}^p\beta^2_j restricts the growth of coefficient estimates.
• \lambda = 0: Parameter estimates not penalised at all, reduces to simple linear regression - obtain the best model which includes all parameters
• \lambda \to \infty: Parameter estimates heavily penalised, coefficients pushed to zero, model is y_i = \hat{\beta}_0
• Note that \beta_0’s estimate is not penalised: Coefficient estimates are heavily scale-variant
• Also called “L^2 regularisation” as the penalty is the square of the \beta_j’s L^2 norm

Lasso regression

Minimise on \beta: \sum_{i=1}^n \Bigl( y_i - \beta_0 - \sum_{j=1}^p \beta_jx_{ij} \Bigr)^2 + \lambda \sum_{j=1}^p |\beta_j| = \text{RSS} + \lambda \sum_{j=1}^p |\beta_j|

• Only difference: penalties placed on absolute value of coefficient estimates
• Can force some of them to exactly zero: significantly easier to interpret model
• Has the effect of also performing some variable selection, like best-subset
• Also called “L^1 regularisation” as the penalty is the \beta_j’s L^1 norm

Note

Before calculating the ridge & lasso penalties, we should standardise all of \boldsymbol{X}’s columns so their sample variances are one. Otherwise we would be penalising some \beta_i’s simply because the ith covariate’s values are relatively bigger or smaller numbers. The R package we use for ridge & lasso regression will do this for you.

Elastic net model

Combines ridge and lasso penalties, so you minimise

\text{RSS} + \lambda \Bigl[ \, \alpha \sum_{j=1}^p |\beta_j| + (1-\alpha) \sum_{j=1}^p \beta_j^2 \, \Bigr]

• \alpha = 1 is lasso, \alpha = 0 is ridge
• 0 < \alpha < 1 is elastic net, a compromise between ridge and lasso

The glmnet package fits elastic net models, so you have to choose \alpha=0 or \alpha=1 to get ridge or lasso. It fits GLMs with the penalties described above.

• “Ridge regression” is just linear regression with a ridge penalty
• “Lasso regression” is just linear regression with a lasso penalty
• Can also do logistic regression, Poisson regression, etc. with a ridge or lasso penalty (the RSS term would change to match the specific GLM model)

Ridge closed-form solution

\boldsymbol{\beta}_\text{LM} = (\boldsymbol{X}^\top\boldsymbol{X})^{-1} \boldsymbol{X}^\top \boldsymbol{y}

model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values + career_opp + comp_benefits + senior_mgmt, data = first_few_rows)
coef(model_subrankings)

      (Intercept) work_life_balance    culture_values        career_opp 
        3.6666667        -0.3333333         0.6666667                NA 
    comp_benefits       senior_mgmt 
               NA                NA 

X <- model.matrix(~ work_life_balance + culture_values + career_opp + comp_benefits + senior_mgmt, data = first_few_rows)
X <- cbind(rep(1, nrow(X)), scale(X[, -1])) # Scale the columns (apart from intercept)
y <- first_few_rows$overall_rating
beta <- solve(t(X) %*% X) %*% t(X) %*% y

Error in solve.default(t(X) %*% X): system is computationally singular: reciprocal condition number = 7.39832e-34

\boldsymbol{\beta}_{\text{Ridge}} = (\boldsymbol{X}^\top\boldsymbol{X} + \lambda\boldsymbol{I})^{-1} \boldsymbol{X}^\top \boldsymbol{y}

ridge <- glmnet(X[,-1], y, alpha = 0, lambda=0.01)
coef(ridge, s=0.01)

6 x 1 sparse Matrix of class "dgCMatrix"
                           s1
(Intercept)        4.33333333
work_life_balance -0.02139038
culture_values     0.12750285
career_opp         0.15892194
comp_benefits      0.17324706
senior_mgmt       -0.15706300

beta <- solve(t(X) %*% X + 0.01 * diag(ncol(X))) %*% t(X) %*% y
beta

                        [,1]
                   4.3189369
work_life_balance -0.0252433
culture_values     0.1338977
career_opp         0.1591410
comp_benefits      0.1691859
senior_mgmt       -0.1581698

Regularisation Plots

Synthetic data example

set.seed(4)
x <- rnorm(50)
y <- x - 2*x^2 + rnorm(100)
data <- data.frame(x = x, y = y)

# Generate true curve
x_grid <- seq(min(x), max(x), length=500)
y_true <- x_grid - 2*x_grid^2
true_curve <- data.frame(x = x_grid, y = y_true)

# Plot the data with the true curve
ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  labs(x = "x", y = "y") +
  theme_minimal()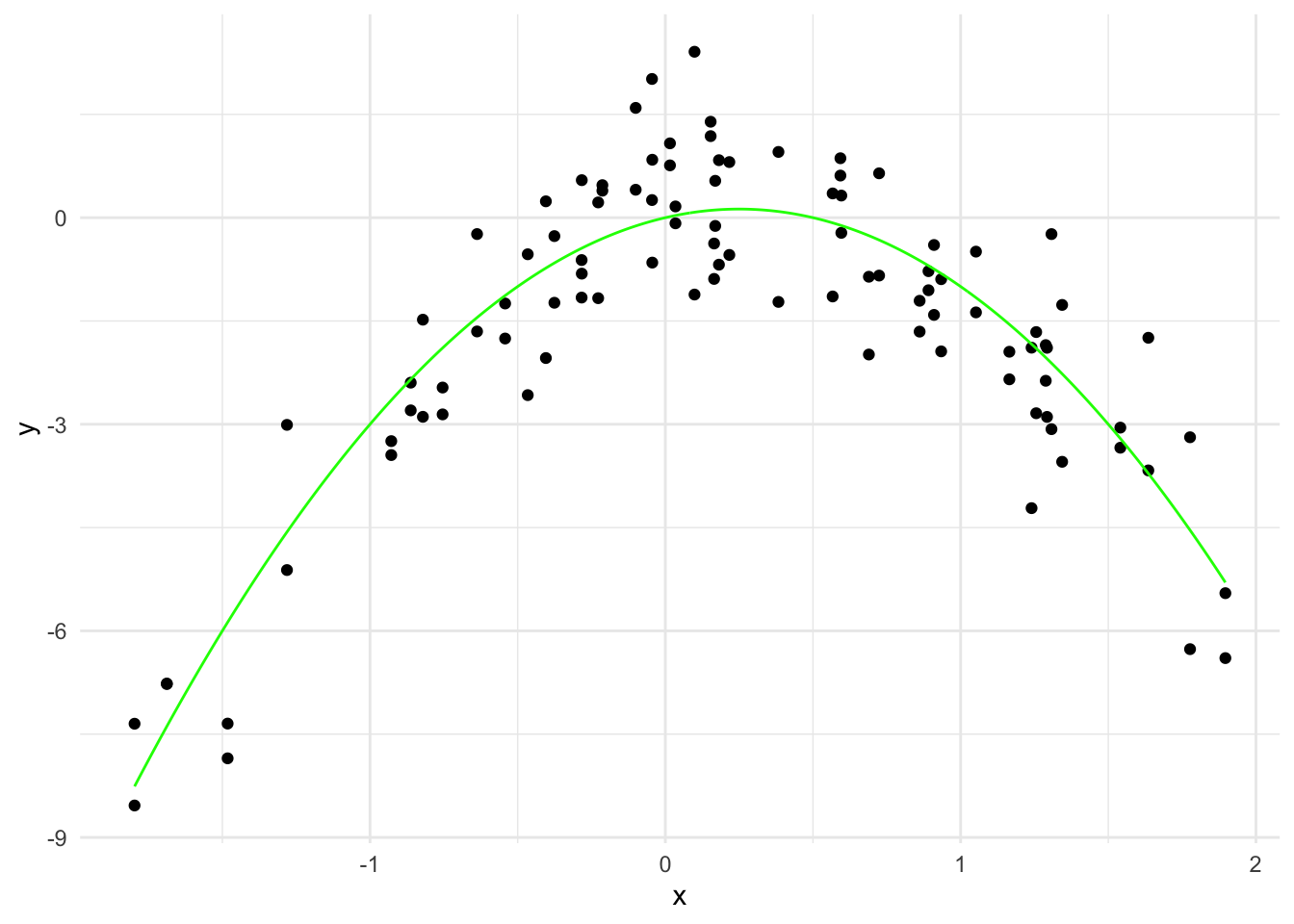

Polynomial regression

# Fit a linear model
linear_model <- lm(y ~ poly(x, 20, raw=TRUE), data = data)

# Generate predictions over the data
y_hat <- predict(linear_model, data.frame(x = x_grid))
linear_predictions <- data.frame(x = x_grid, y = y_hat)

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = linear_predictions, aes(x = x, y = y), color = "red") +
  labs(x = "x", y = "y") +
  theme_minimal()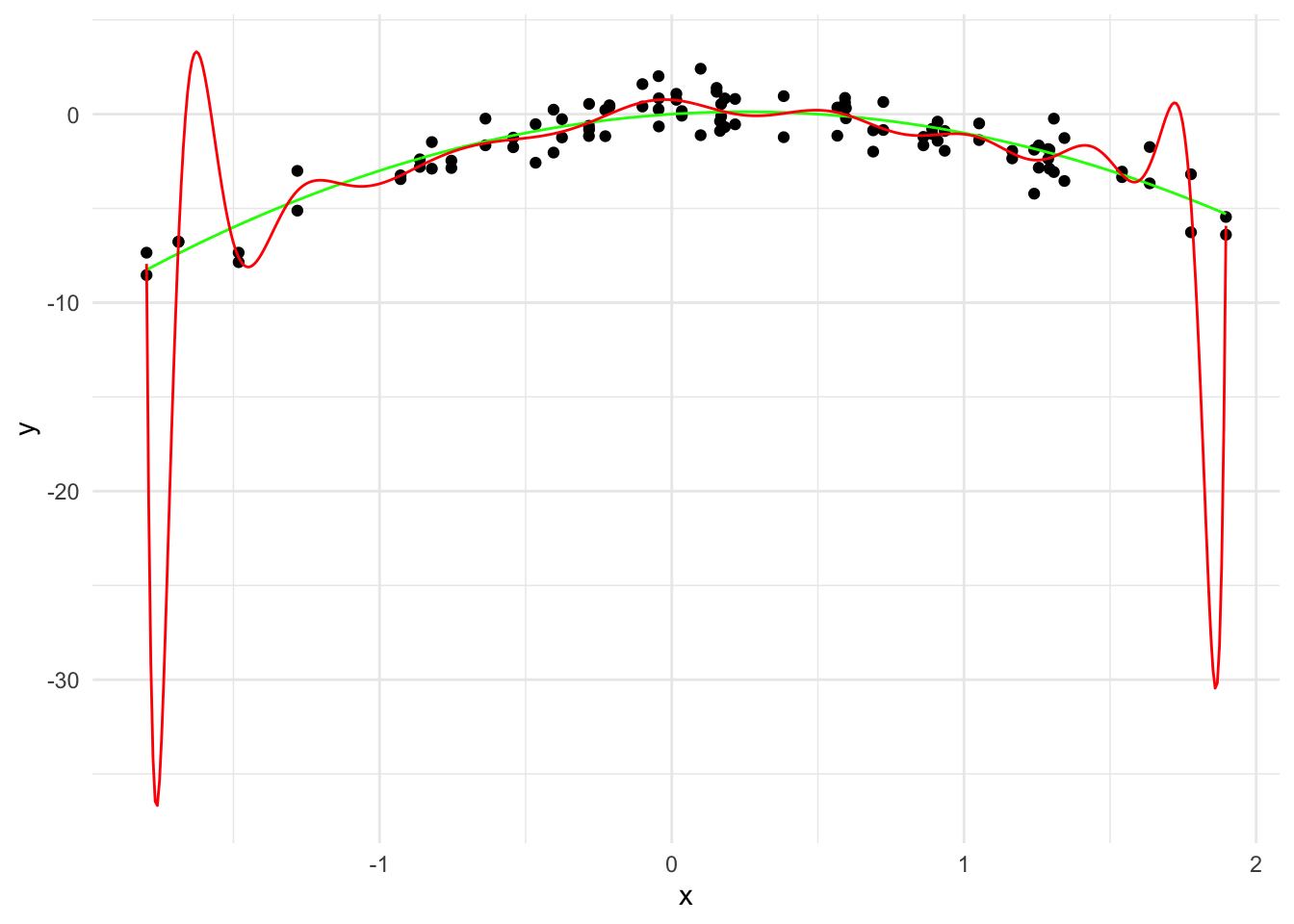

\hat{y}(x) = 0.76 - 1.09 x - 22.91 x^2 + \cdots - 1.77 x^{19} + 2.15 x^{20}

The \sum_{j=1}^{20} \hat{\beta}_j^2 is 6970618.

Ridge regression with \lambda = 0.01

# Create a data frame with the predictors
x_poly <- model.matrix(~ poly(x, 20, raw=TRUE), data = data)[, -1]
x_grid_poly <- model.matrix(~ poly(x_grid, 20, raw=TRUE))[, -1]
colnames(x_grid_poly) <- colnames(x_poly)

ridge_model <- glmnet(x_poly, y, alpha = 0, lambda=c(0.01, 0.1, 1, 10))

# Generate predictions over the data
y_hat <- predict(ridge_model, newx=x_grid_poly, s = 0.01)
linear_predictions <- data.frame(x = x_grid, y = y_hat)
names(linear_predictions) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = linear_predictions, aes(x = x, y = y), color = "red") +
  labs(x = "x", y = "y") +
  theme_minimal()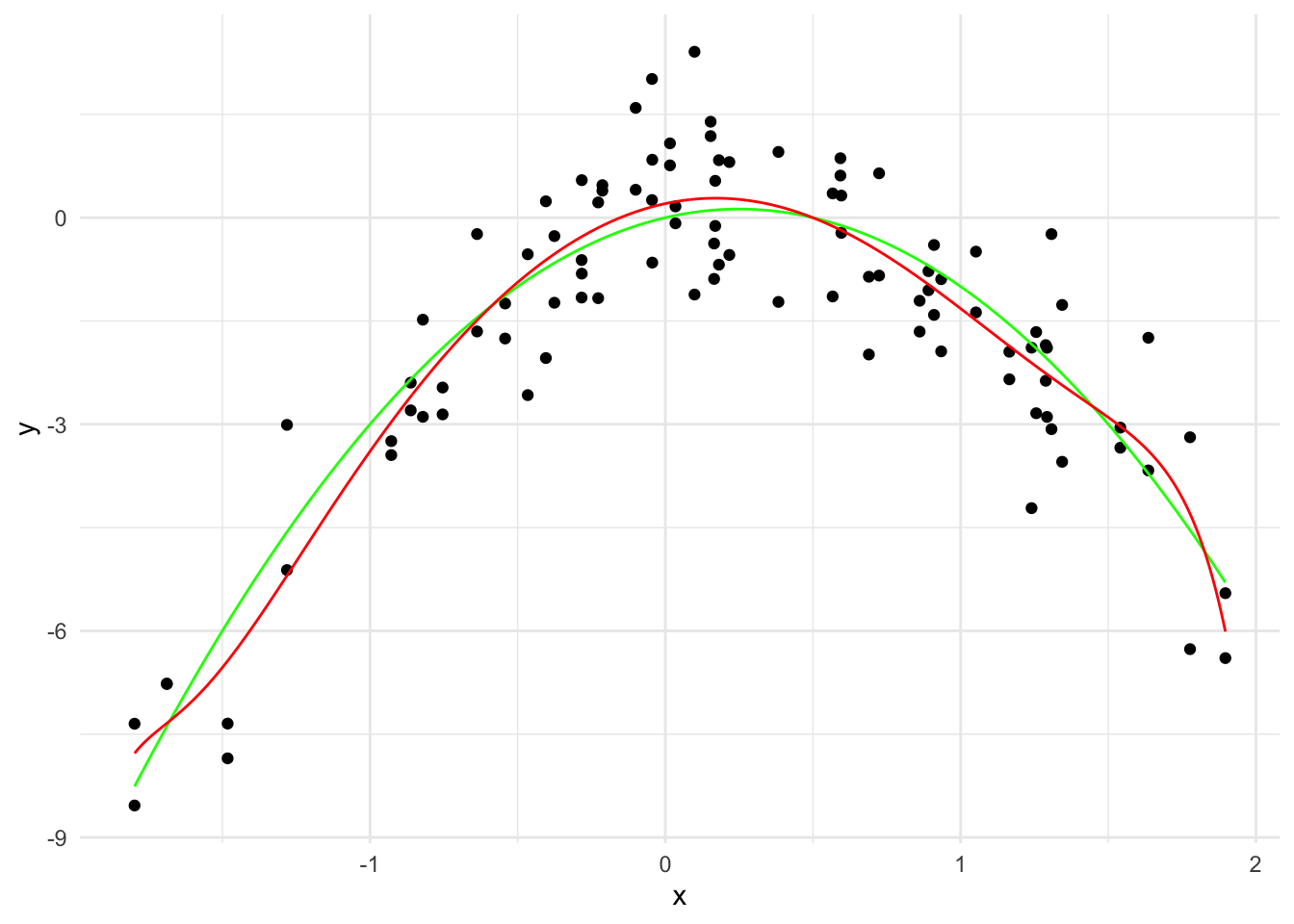

\hat{y}(x) = 0.20 + 0.92 x - 2.73 x^2 + \cdots + 0.000007 x^{19} - 0.000003 x^{20}

The \sum_{j=1}^{20} \hat{\beta}_j^2 is 8.31.

Ridge regression with \lambda = 0.1

y_hat_0_1 <- predict(ridge_model, x_grid_poly, s = 0.1)
ridge_predictions_0_1 <- data.frame(x = x_grid, y = y_hat_0_1)
names(ridge_predictions_0_1) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = ridge_predictions_0_1, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()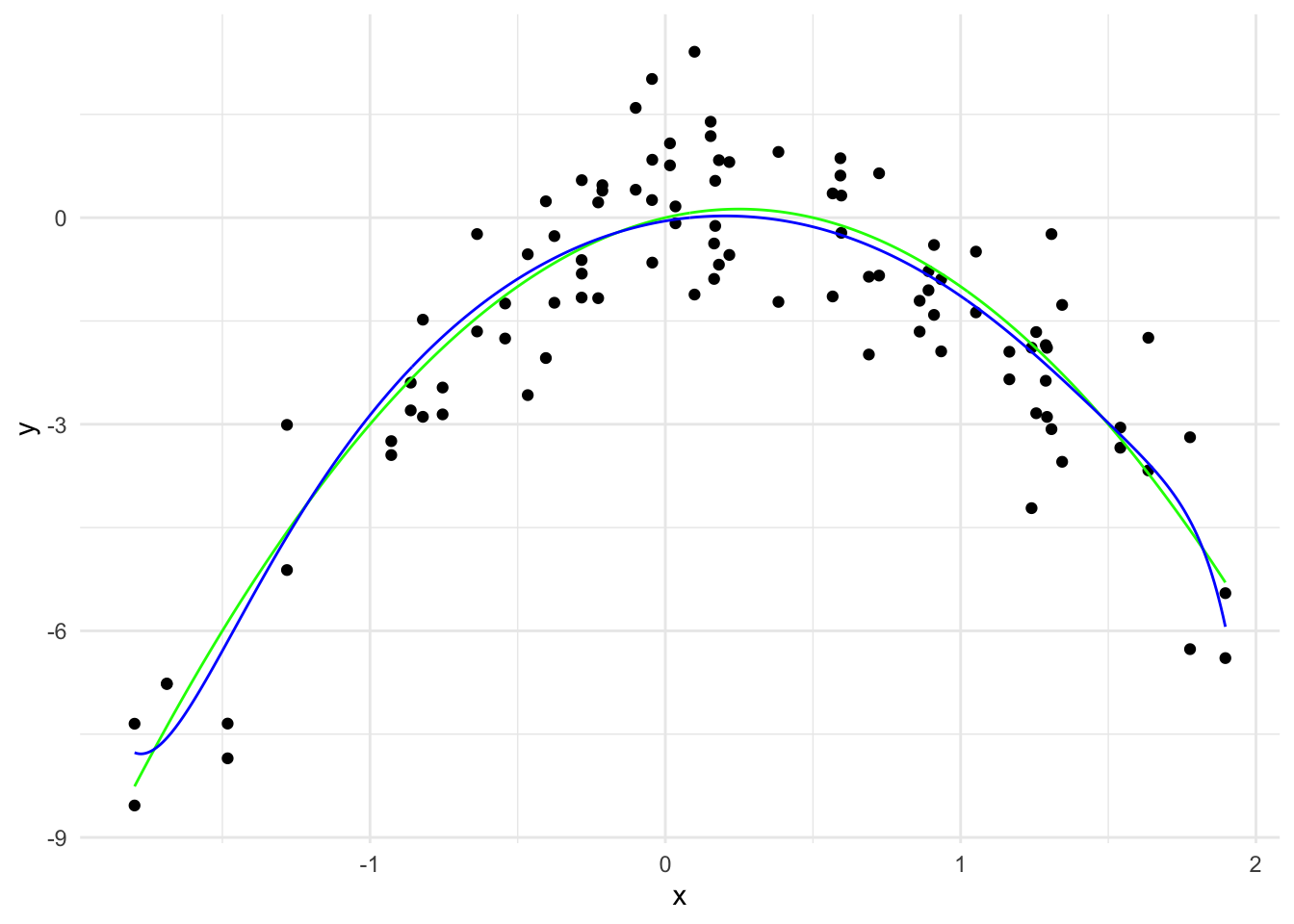

\hat{y}(x) = -0.05 + 0.73 x - 1.82 x^2 + \cdots - 0.000004 x^{19} - 0.000001 x^{20}

The \sum_{j=1}^{20} \hat{\beta}_j^2 is 3.86.

Ridge regression with \lambda = 1

y_hat_1 <- predict(ridge_model, x_grid_poly, s = 1)
ridge_predictions_1 <- data.frame(x = x_grid, y = y_hat_1)
names(ridge_predictions_1) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = ridge_predictions_1, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()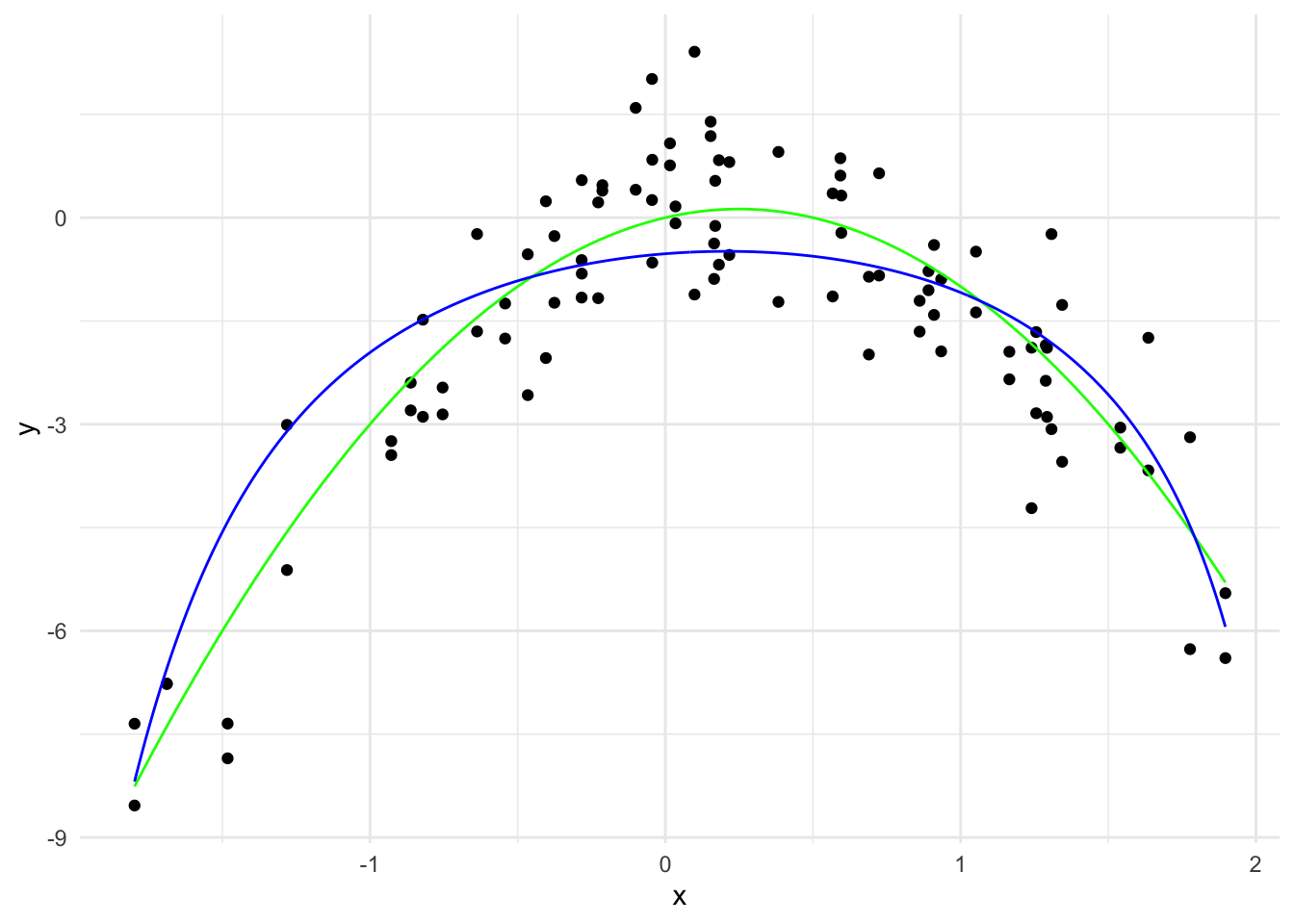

\hat{y}(x) = -0.52 + 0.34 x - 0.82 x^2 + \cdots - 0.0000006 x^{19} + 0.00000007 x^{20}

The \sum_{j=1}^{20} \hat{\beta}_j^2 is 0.818.

Ridge regression with \lambda = 10

y_hat_10 <- predict(ridge_model, x_grid_poly, s = 10)
ridge_predictions_10 <- data.frame(x = x_grid, y = y_hat_10)
names(ridge_predictions_10) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = ridge_predictions_10, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()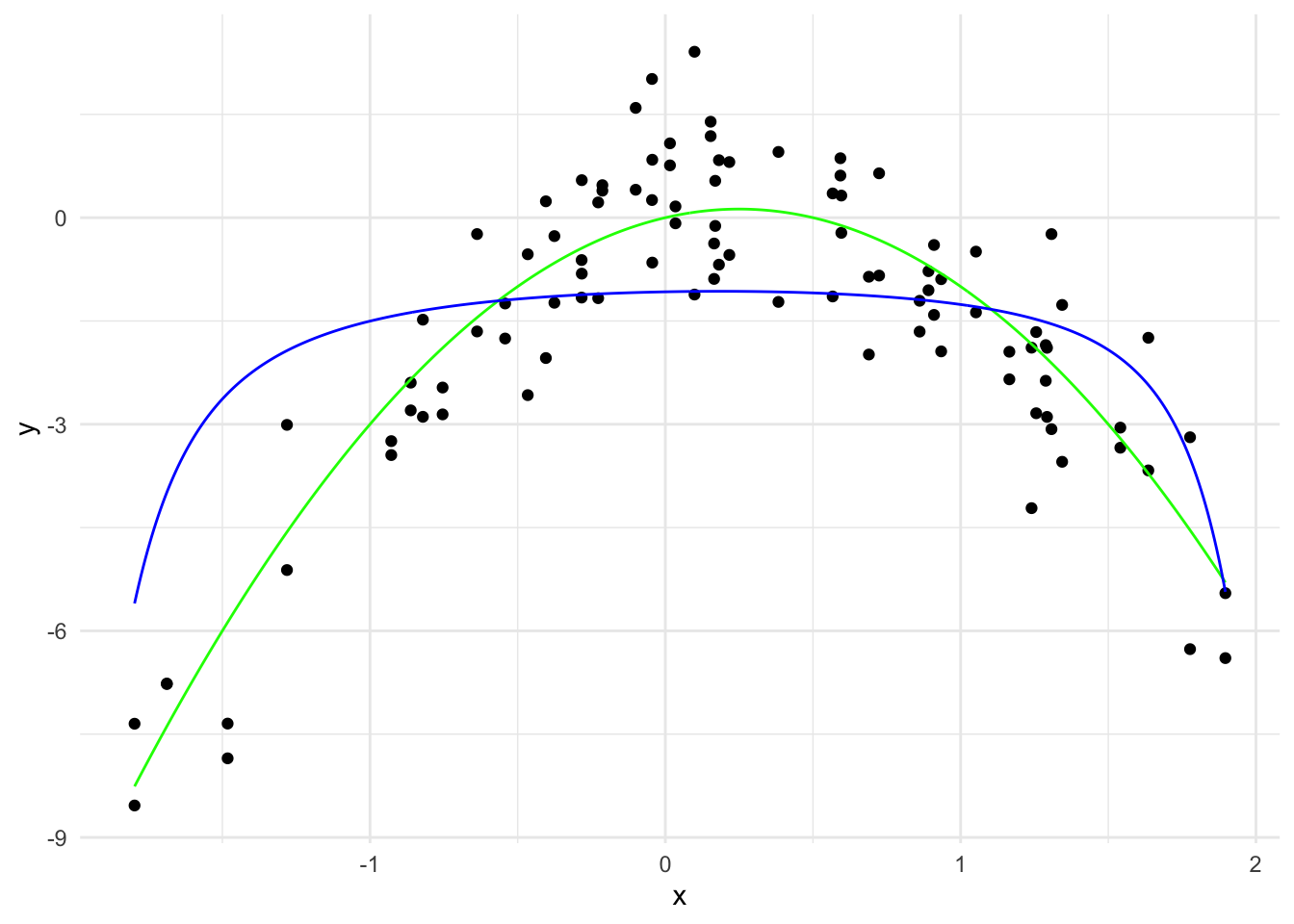

\hat{y}(x) = -1.08 + 0.08 x - 0.23 x^2 + \cdots + 0.0000003 x^{19} - 0.000001 x^{20}

The \sum_{j=1}^{20} \hat{\beta}_j^2 is 0.0624.

Regularisation path plots

ridge_model <- glmnet(x_poly, y, alpha=0)
plot(ridge_model, xvar="lambda", label=TRUE)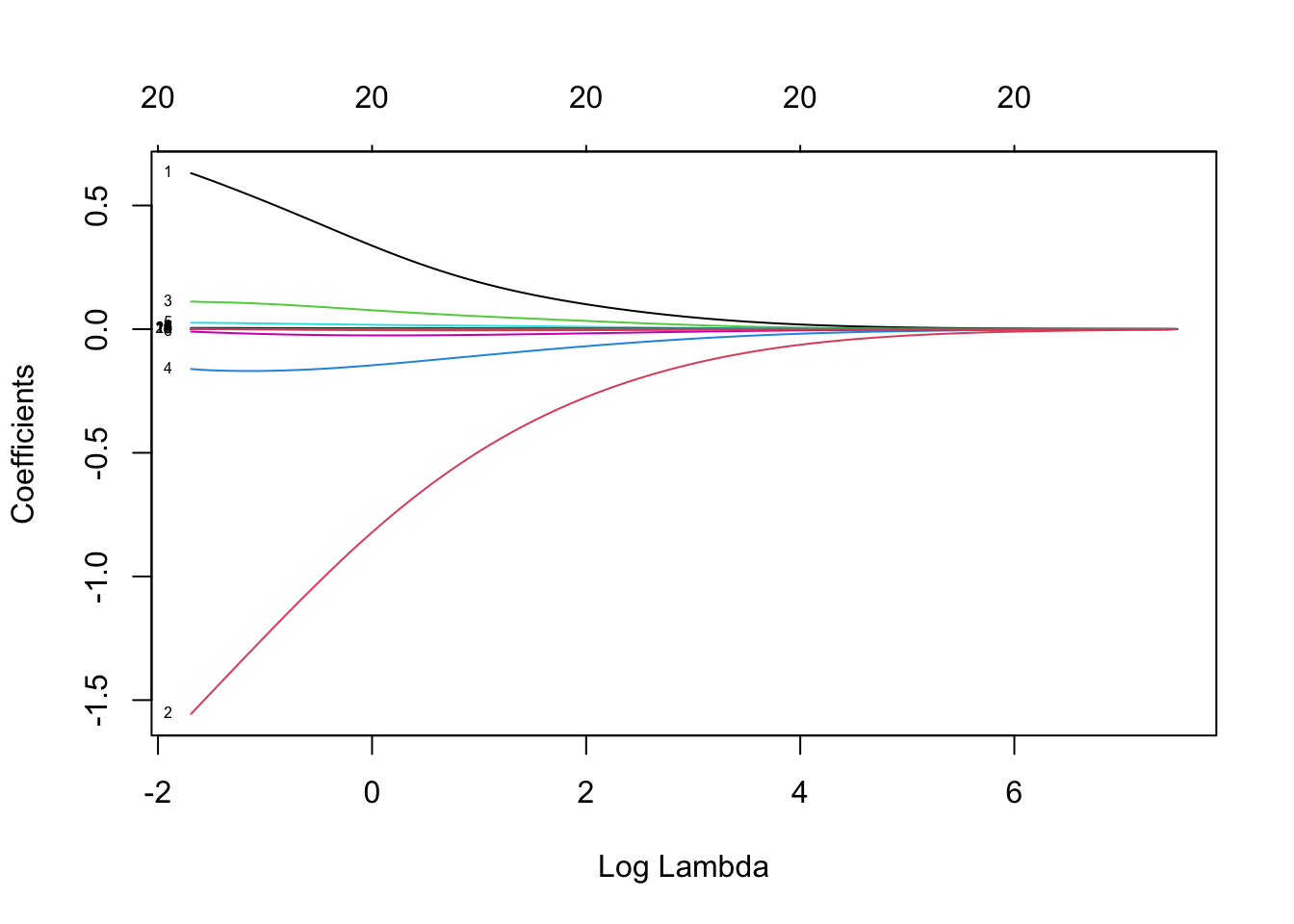

Cross-validation errors

# Find the best lambda
cv_out <- cv.glmnet(x_poly, y, alpha = 0)
plot(cv_out)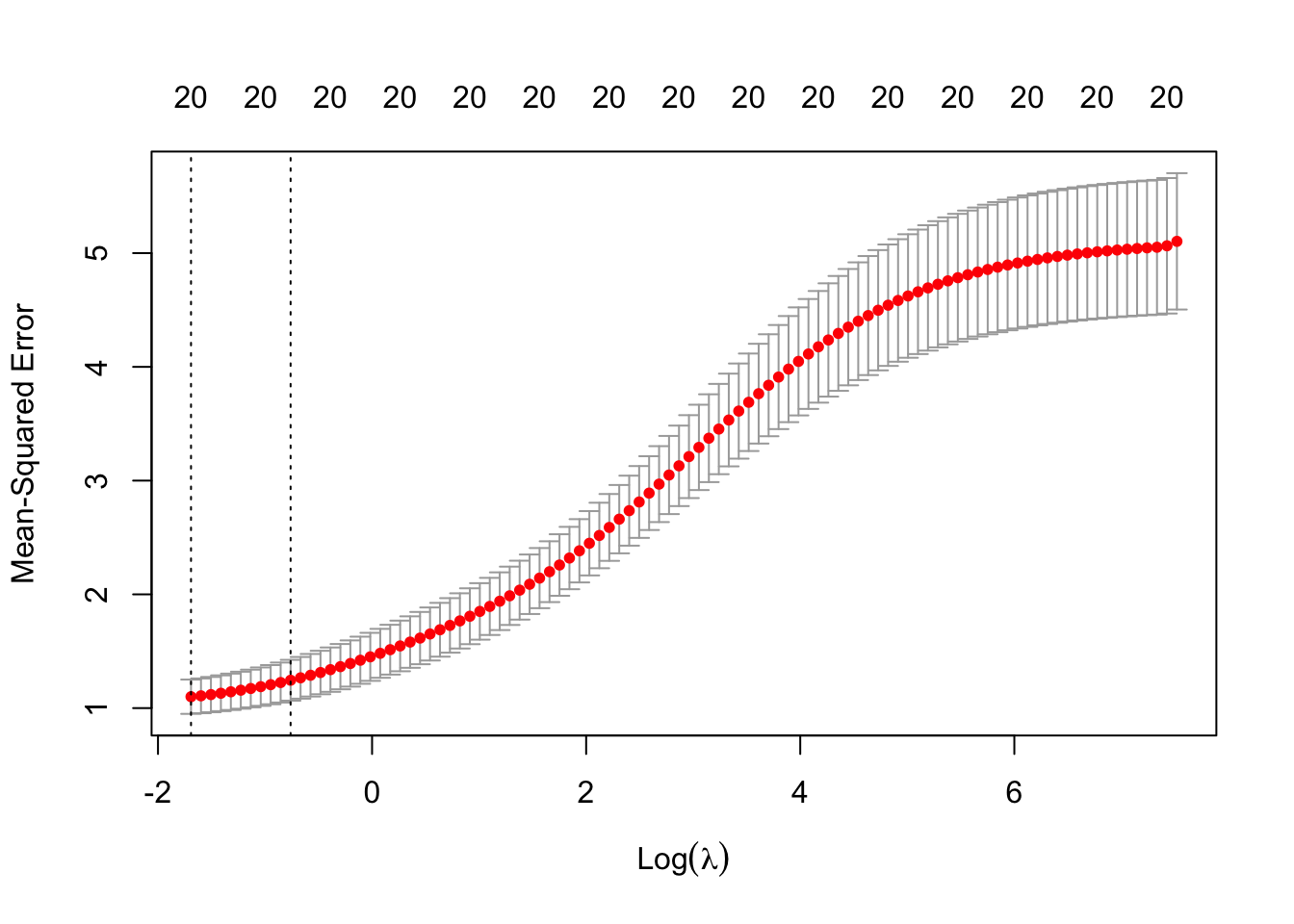

The \lambda which minimises the CV MSE is 0.1842555 (\log(\lambda) is -1.6914321).

Lasso regression with \lambda = 0.01

lasso_model <- glmnet(x_poly, y, alpha = 1, lambda=c(0.01, 0.1, 1, 10))

# Generate predictions over the data
y_hat <- predict(lasso_model, newx=x_grid_poly, s = 0.01)
linear_predictions <- data.frame(x = x_grid, y = y_hat)
names(linear_predictions) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = linear_predictions, aes(x = x, y = y), color = "red") +
  labs(x = "x", y = "y") +
  theme_minimal()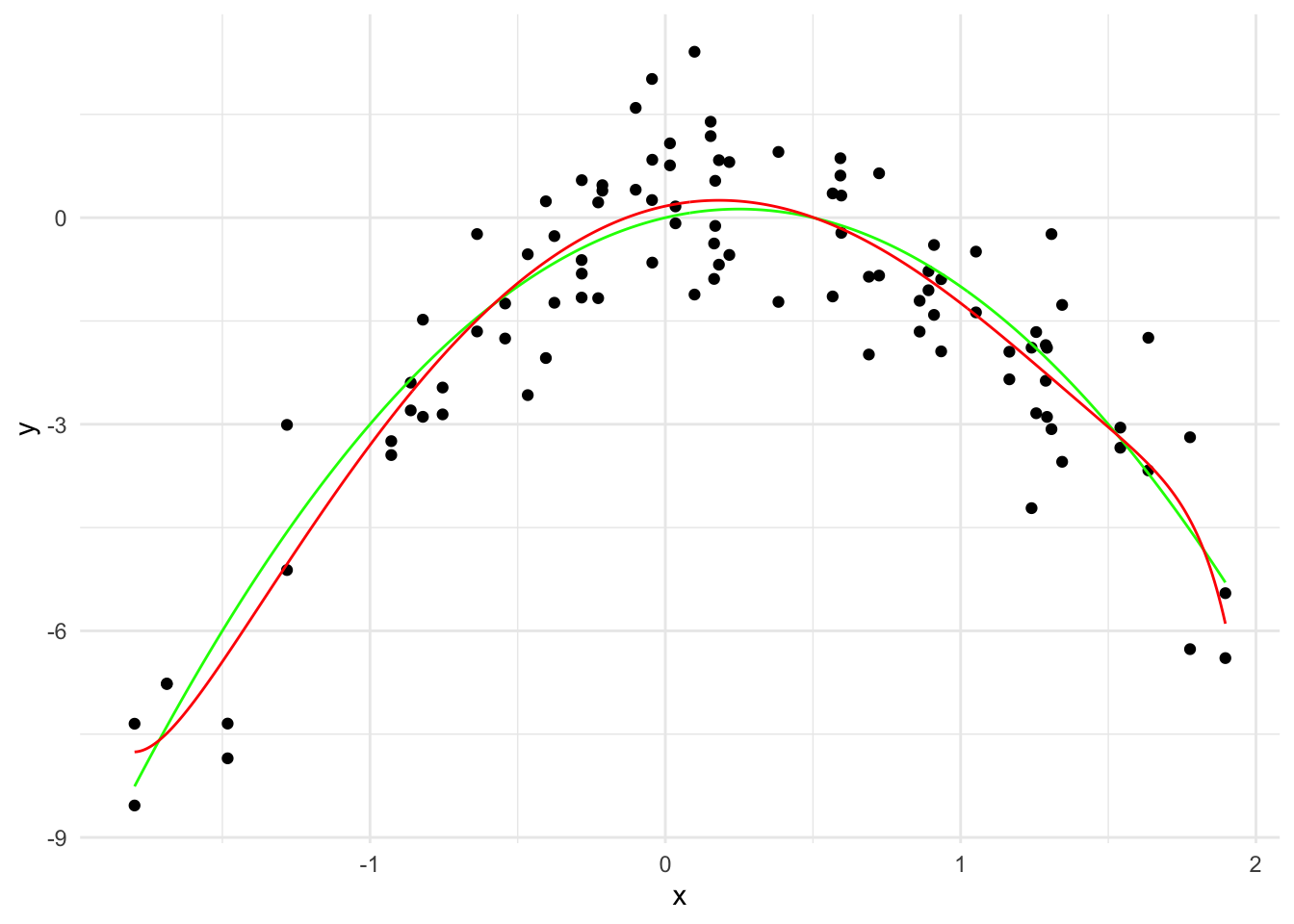

\hat{y}(x) = 0.17 + 0.93 x - 2.60 x^2 + \cdots - 3.29 \times 10^{-6} x^{19} - 5.95 \times 10^{-7} x^{20}

The \sum_{j=1}^{20} |\hat{\beta}_j| is 3.79 and there are 8 non-zero coefficients.

Lasso regression with \lambda = 0.1

y_hat_0_1 <- predict(lasso_model, x_grid_poly, s = 0.1)
lasso_predictions_0_1 <- data.frame(x = x_grid, y = y_hat_0_1)
names(lasso_predictions_0_1) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = lasso_predictions_0_1, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()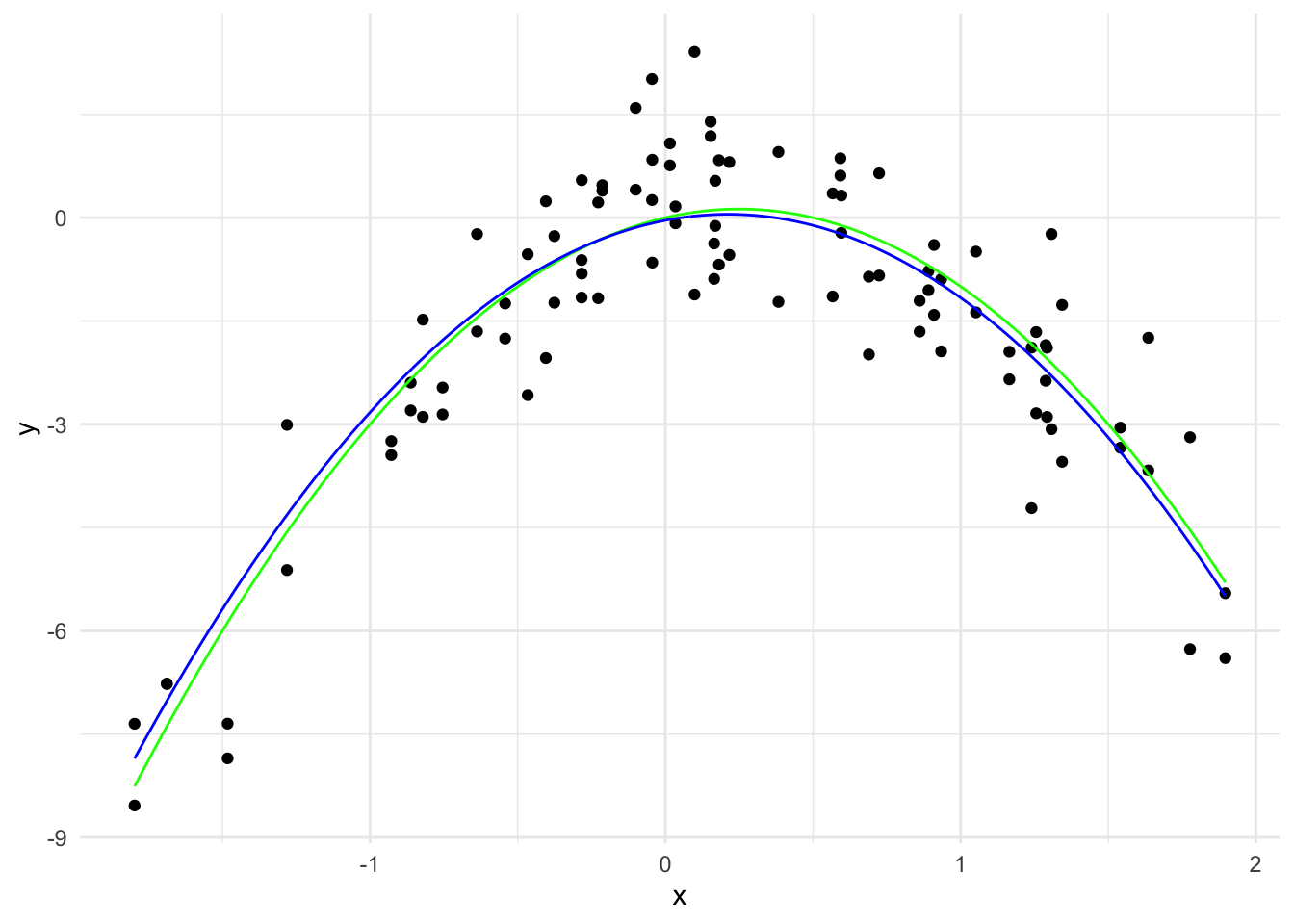

\hat{y}(x) = -0.04 + 0.83 x - 1.96 x^2

The \sum_{j=1}^{20} |\hat{\beta}_j| is 2.79 and there are 2 non-zero coefficients.

Lasso regression with \lambda = 1

y_hat_1 <- predict(lasso_model, x_grid_poly, s = 1)
lasso_predictions_1 <- data.frame(x = x_grid, y = y_hat_1)
names(lasso_predictions_1) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = lasso_predictions_1, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()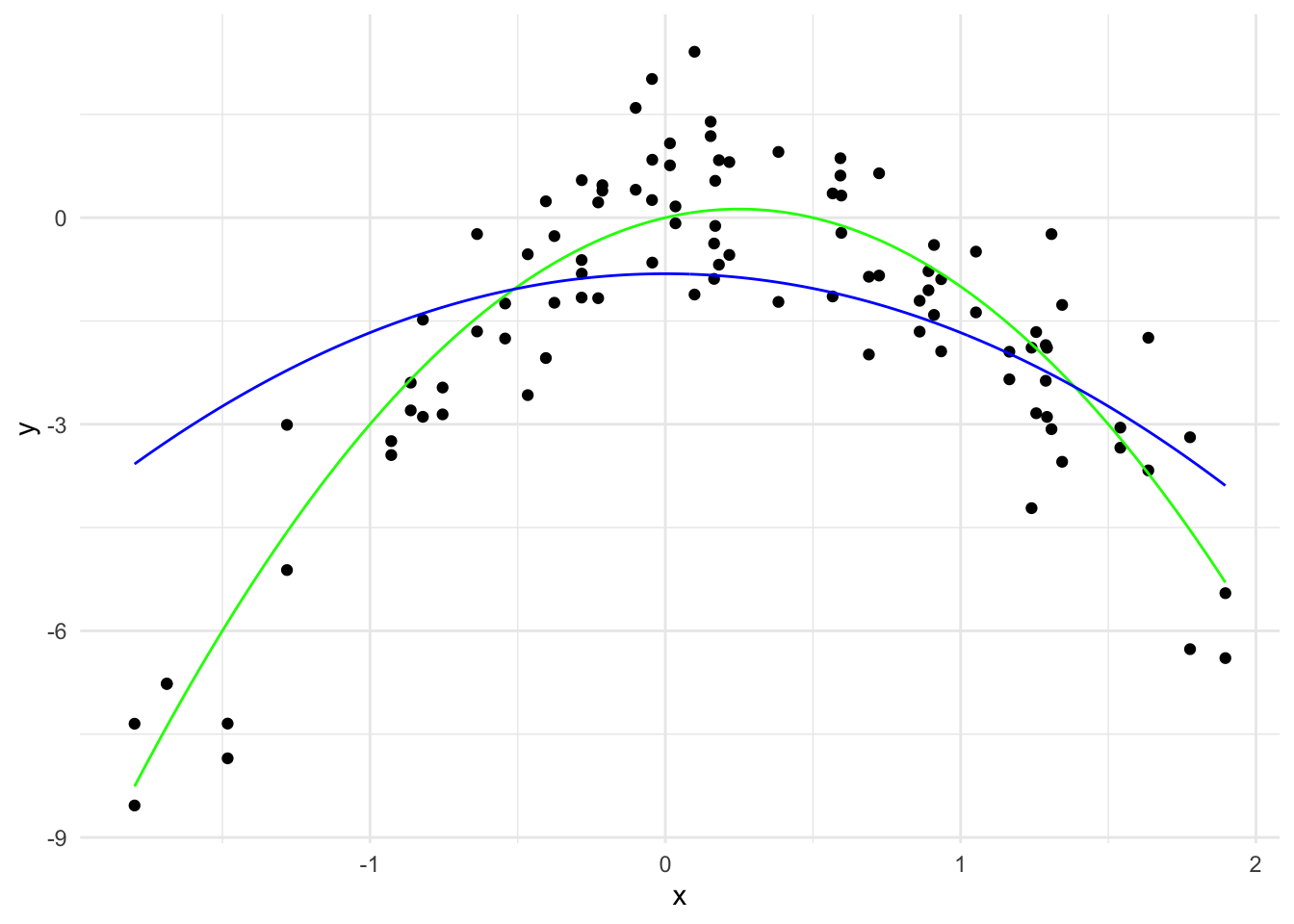

\hat{y}(x) = -0.81 - 0.86 x^2

The \sum_{j=1}^{20} |\hat{\beta}_j| is 0.855 and there are 1 non-zero coefficients.

Lasso regression with \lambda = 10

y_hat_10 <- predict(lasso_model, x_grid_poly, s = 10)
lasso_predictions_10 <- data.frame(x = x_grid, y = y_hat_10)
names(lasso_predictions_10) <- c("x", "y")

ggplot(data, aes(x = x, y = y)) +
  geom_point() +
  geom_line(data = true_curve, aes(x = x, y = y), color = "green") +
  geom_line(data = lasso_predictions_10, aes(x = x, y = y), color = "blue") +
  labs(x = "x", y = "y") +
  theme_minimal()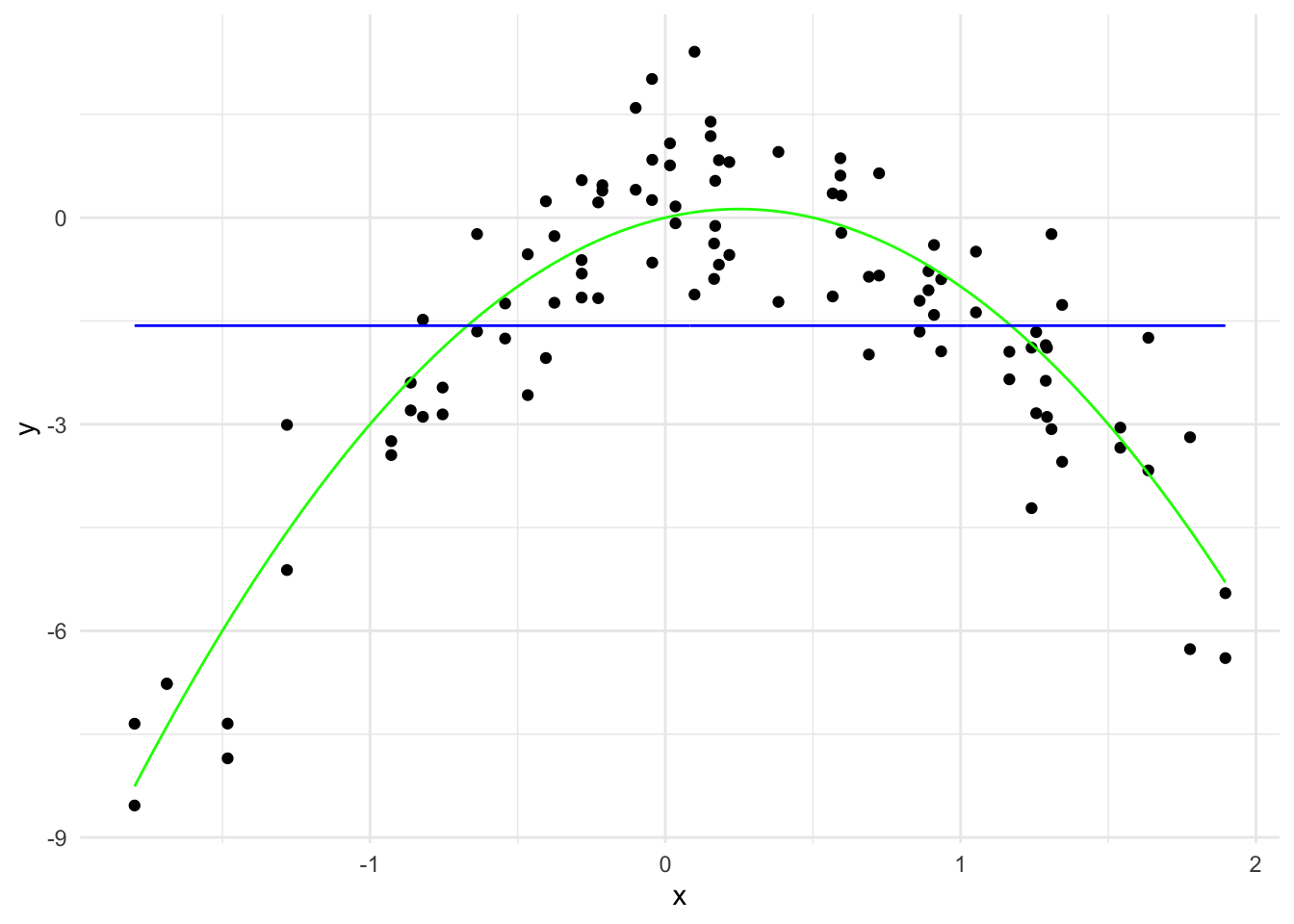

\hat{y}(x) = -1.57 - 1.90 \times 10^{-16} x^2

The \sum_{j=1}^{20} |\hat{\beta}_j| is 1.9e-16 and there is 1 non-zero coefficient.

Regularisation path plots

lasso_model <- glmnet(x_poly, y, alpha=1)
plot(lasso_model, xvar="lambda", label=TRUE)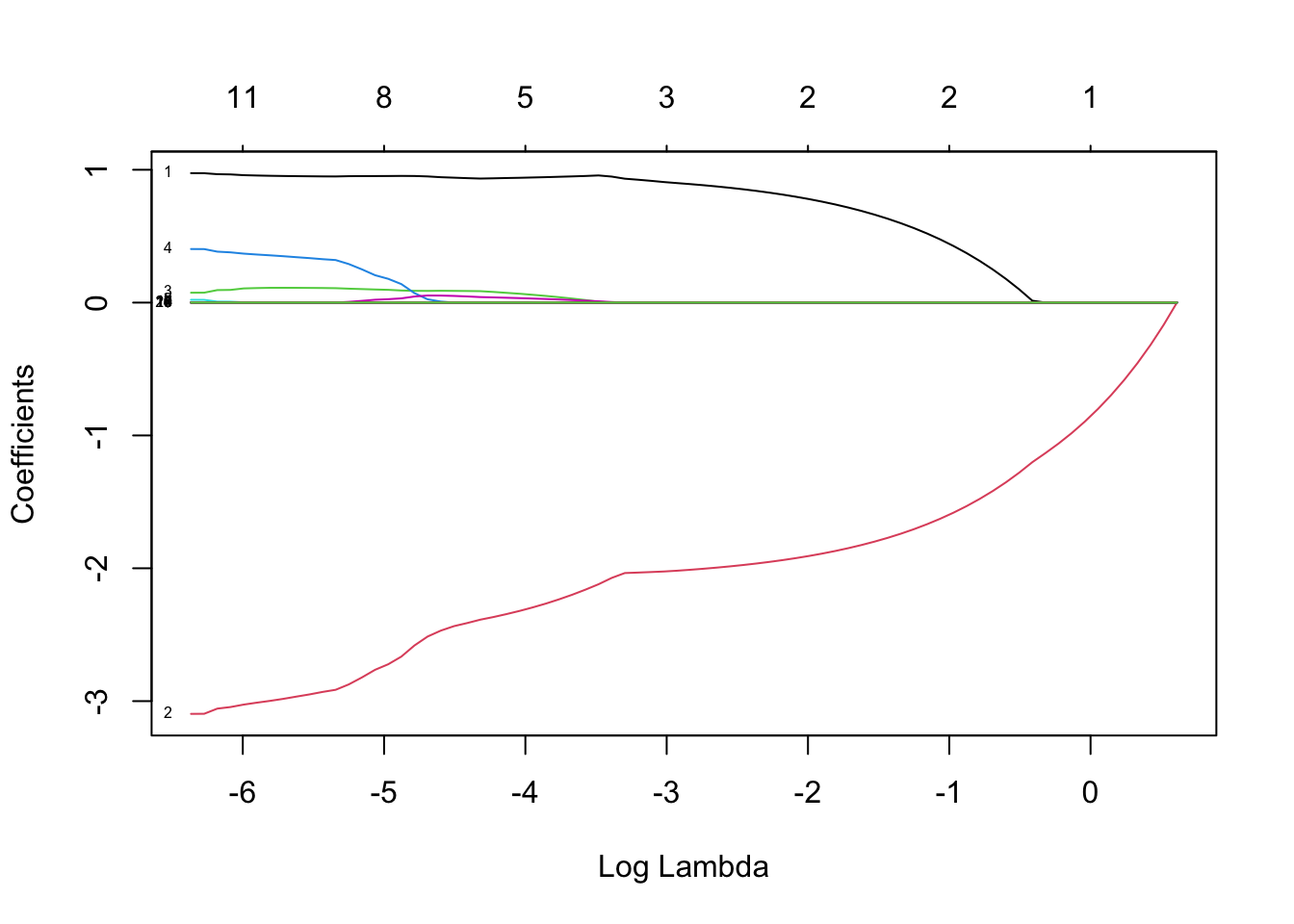

Cross-validation errors

# Find the best lambda
cv_out <- cv.glmnet(x_poly, y, alpha = 1)

# Plot the cross-validated error
plot(cv_out)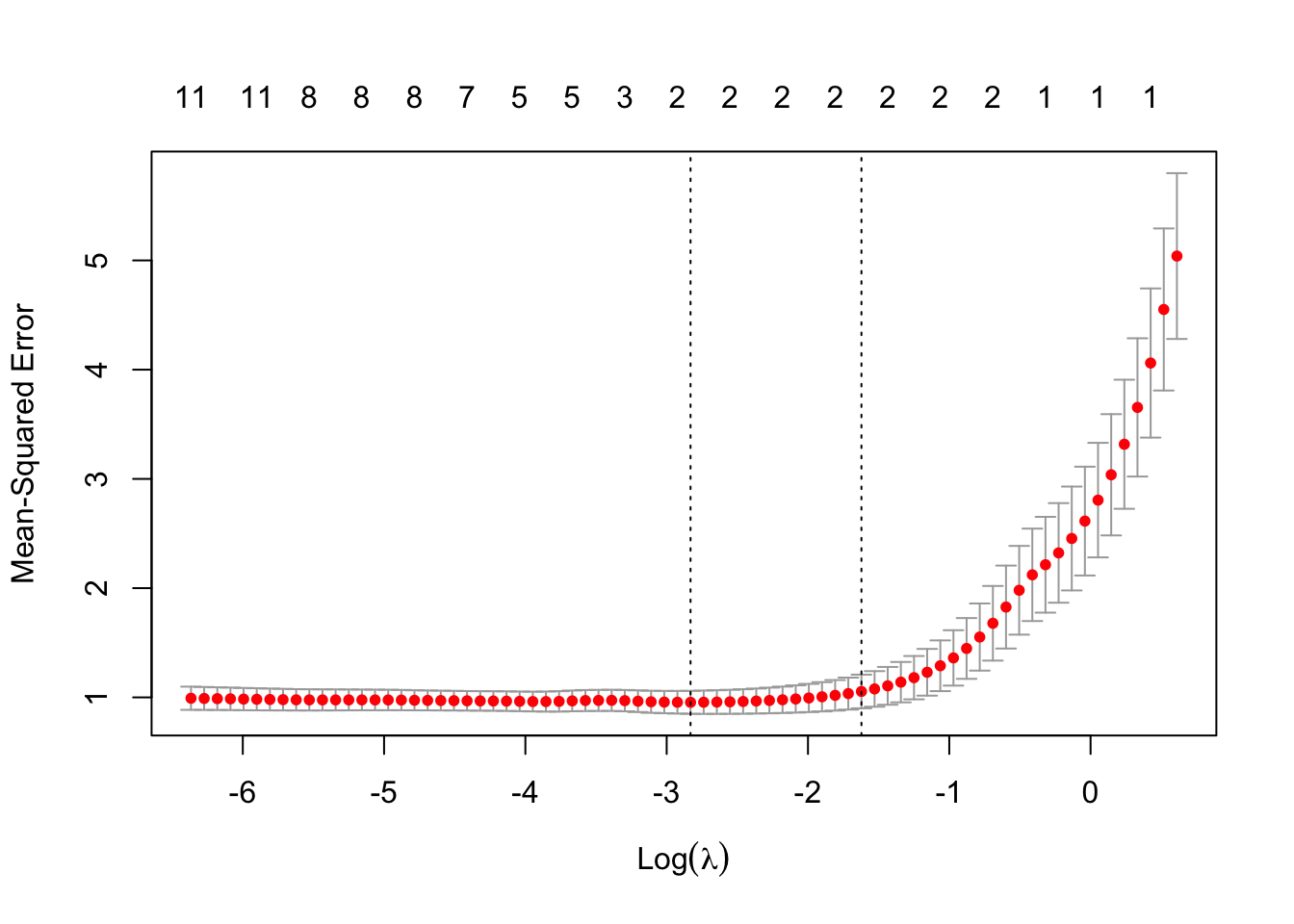

The \lambda which minimises the CV MSE is 0.0589482 (\log(\lambda) is -2.8310954).

Regularisation Demos

Glassdoor preparation

set.seed(123)
test_index <- sample(1:nrow(df_uni), 0.2 * nrow(df_uni))
test <- df_uni[test_index, ]
train_val <- df_uni[-test_index, ]

model_subrankings <- lm(overall_rating ~ work_life_balance + culture_values +
        career_opp + comp_benefits + senior_mgmt +
        recommend + ceo_approv, data = train_val)
summary(model_subrankings)

Call:
lm(formula = overall_rating ~ work_life_balance + culture_values + 
    career_opp + comp_benefits + senior_mgmt + recommend + ceo_approv, 
    data = train_val)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.0109 -0.3441 -0.0248  0.3595  3.4854 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)         1.321466   0.032022  41.267  < 2e-16 ***
work_life_balance   0.068873   0.006287  10.954  < 2e-16 ***
culture_values      0.244629   0.007812  31.314  < 2e-16 ***
career_opp          0.175851   0.006339  27.741  < 2e-16 ***
comp_benefits       0.070892   0.006010  11.796  < 2e-16 ***
senior_mgmt         0.177644   0.007244  24.521  < 2e-16 ***
recommendPositive   0.121017   0.017635   6.862 7.19e-12 ***
recommendNegative  -0.544801   0.025401 -21.448  < 2e-16 ***
ceo_approvPositive -0.020925   0.016648  -1.257  0.20884    
ceo_approvMild     -0.047943   0.016599  -2.888  0.00388 ** 
ceo_approvNegative -0.128851   0.028392  -4.538 5.74e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5638 on 9689 degrees of freedom
Multiple R-squared:  0.7169,    Adjusted R-squared:  0.7166 
F-statistic:  2454 on 10 and 9689 DF,  p-value: < 2.2e-16

X <- model.matrix(overall_rating ~ work_life_balance + culture_values +
        career_opp + comp_benefits + senior_mgmt +
        recommend + ceo_approv, data = train_val)[,-1]
y <- train_val$overall_rating

Glassdoor ridge regression

ridge <- glmnet(X, y, alpha = 0)
plot(ridge, xvar="lambda", label=TRUE)

Glassdoor ridge regression CV

cv_ridge <- cv.glmnet(X, y, alpha = 0)
plot(cv_ridge)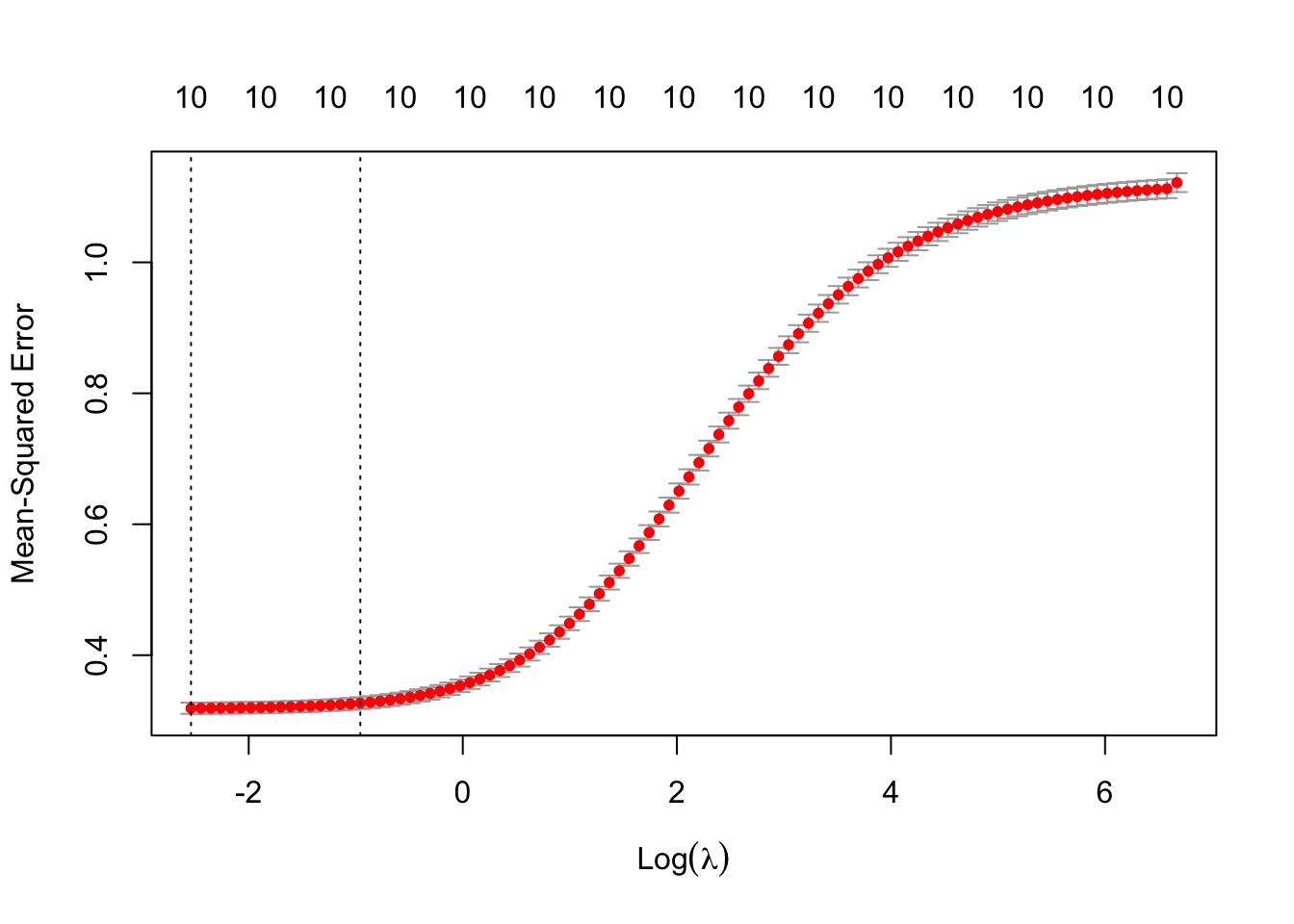

The \lambda which minimises the CV MSE is 0.0789461 (\log(\lambda) is -2.5389899).

Glassdoor lasso regression

lasso <- glmnet(X, y, alpha = 1)
plot(lasso, xvar="lambda", label=TRUE)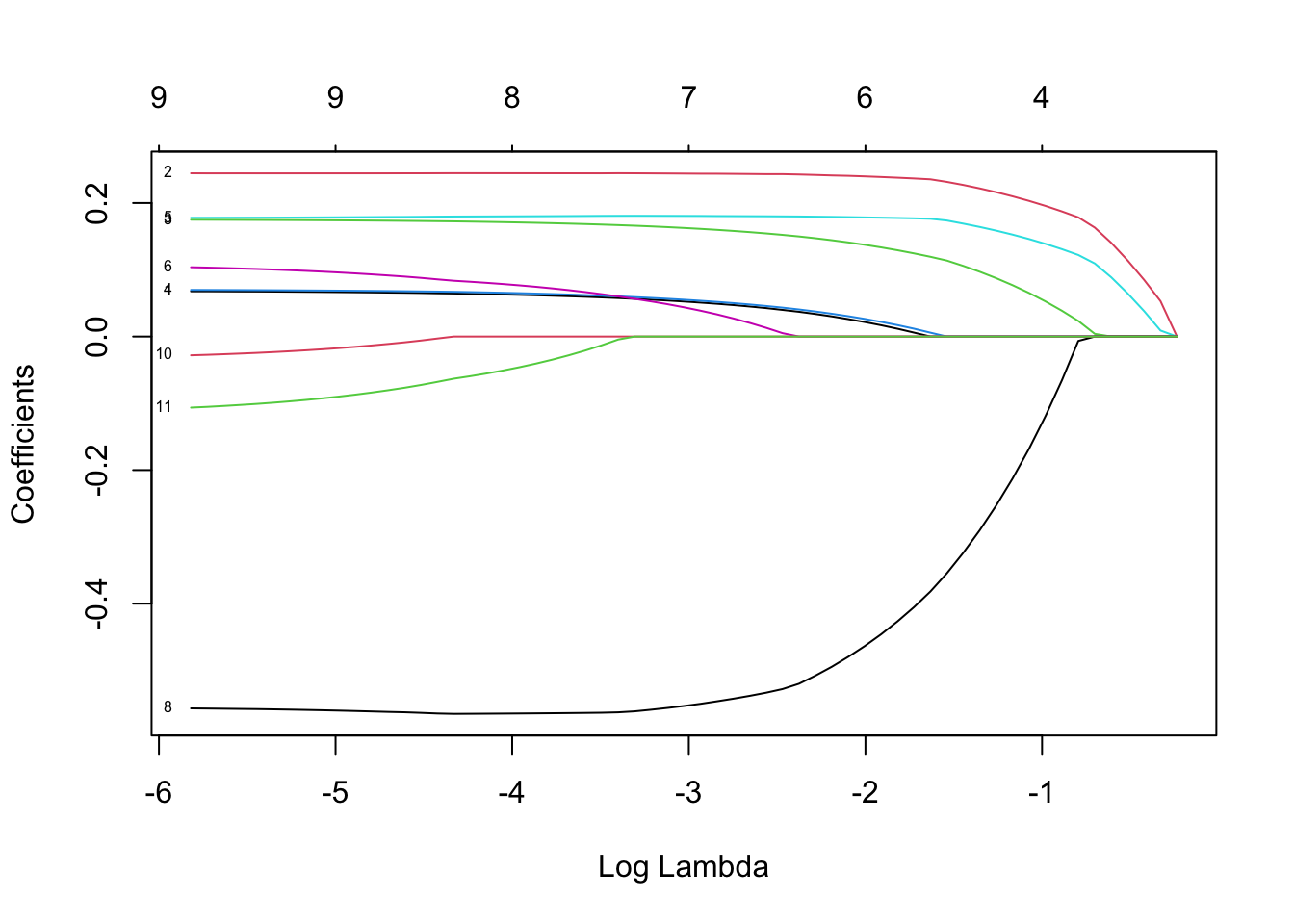

Glassdoor lasso regression CV

cv_lasso <- cv.glmnet(X, y, alpha = 1)
plot(cv_lasso)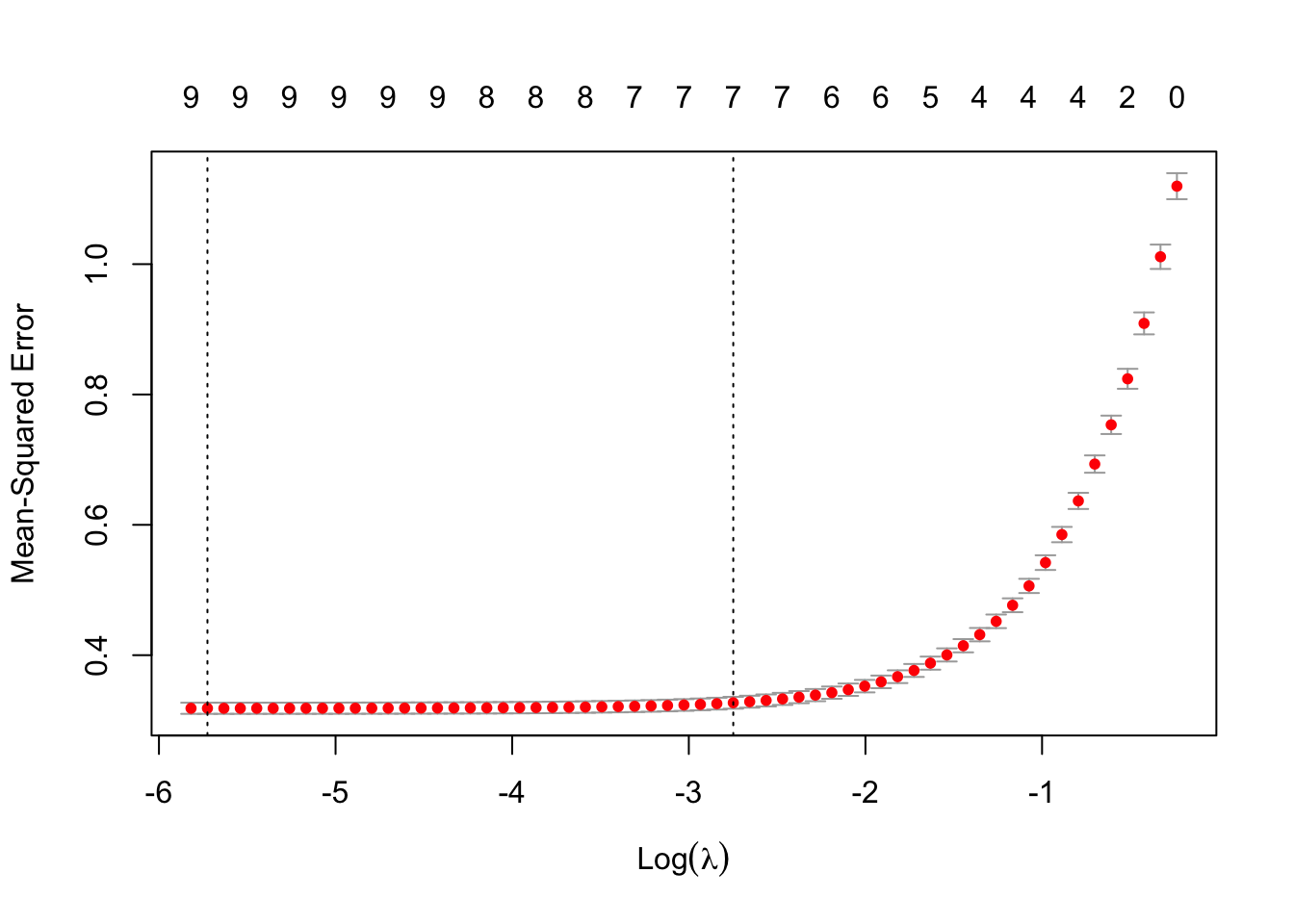

The \lambda which minimises the CV MSE is 0.0032621 (\log(\lambda) is -5.7253955).

The “one standard error” model

“lambda.min”: the \lambda at which the smallest MSE is achieved.

“lambda.1se”: the largest \lambda at which the MSE is within one standard error of the smallest MSE (default).

coef(cv_lasso, s = "lambda.min")

12 x 1 sparse Matrix of class "dgCMatrix"
                            s1
(Intercept)         1.33348345
work_life_balance   0.06771192
culture_values      0.24444863
career_opp          0.17493054
comp_benefits       0.06970145
senior_mgmt         0.17788762
recommendPositive   0.10325936
recommendMild       .         
recommendNegative  -0.55711640
ceo_approvPositive  .         
ceo_approvMild     -0.02732177
ceo_approvNegative -0.10528624

coef(cv_lasso, s = "lambda.1se")

12 x 1 sparse Matrix of class "dgCMatrix"
                            s1
(Intercept)         1.57364673
work_life_balance   0.04712771
culture_values      0.24371243
career_opp          0.15818381
comp_benefits       0.05006640
senior_mgmt         0.18033404
recommendPositive   0.02714509
recommendMild       .         
recommendNegative  -0.54238656
ceo_approvPositive  .         
ceo_approvMild      .         
ceo_approvNegative  .         

Source: Hastie et al. (2023), An Introduction to glmnet.

Gene expression data

load_gene_data <- function() {
  # Read in the information about the study participants
  labels <- read.csv("2912Table2.csv", header = TRUE)
  er <- labels[,14]
  n <- nrow(labels)
  n1 <- sum(er)  # Should be 65
  n2 <- n - n1   # Should be 99-65=34
  
  # Read in the gene expressions, remove meta-info and NA rows
  genes <- read.csv("2912Table3.csv", header = TRUE)
  genes <- genes[ , -(1:6)]
  genes <- t(as.matrix(genes[rowSums(is.na(genes)) == 0, ]))
  
  df <- as.data.frame(genes)
  df$er <- er
  df
}

df <- load_gene_data()
df

# A tibble: 99 × 4,405
       `8`   `18`    `20`   `21`   `22`    `26`    `27`    `28`   `29`   `30`
     <dbl>  <dbl>   <dbl>  <dbl>  <dbl>   <dbl>   <dbl>   <dbl>  <dbl>  <dbl>
 1  0.0164 -0.294 -0.166   0.423 -0.507 -0.559  -0.679  -0.123  -0.511 -0.837
 2 -0.435  -0.270  0.0251  0.474 -0.662 -0.678  -0.0576  0.396  -0.247 -0.705
 3 -0.327  -0.735 -0.0805  0.649 -0.786 -0.0397 -0.238  -0.851  -0.501 -0.820
 4  0.496  -0.389 -0.121  -0.227 -0.776  0.0559  0.0206 -0.683  -0.542 -0.995
 5  1.37   -0.192 -0.0716  0.265 -0.666 -0.342   0.180  -0.862  -0.386 -0.797
 6 -0.191  -0.232  0.547   0.287 -0.708 -0.250   0.355  -0.0872 -0.524 -0.890
 7  0.264  -0.424  0.259   1.98  -0.386  0.109   0.258  -0.749  -0.220 -0.789
 8 -0.537  -0.152  0.660   0.303 -0.778 -0.791  -0.0715 -0.517  -0.299 -0.866
 9  0.197  -0.292  0.173   2.17  -0.272 -0.819  -0.0359 -0.293  -0.232 -0.590
10  0.0915 -0.107  0.0381  2.44  -0.152  0.345   0.245   0.451  -0.103 -0.414
# ℹ 89 more rows
# ℹ 4,395 more variables: `32` <dbl>, `33` <dbl>, `35` <dbl>, `37` <dbl>,
#   `38` <dbl>, `39` <dbl>, `40` <dbl>, `42` <dbl>, `43` <dbl>, `44` <dbl>,
#   `45` <dbl>, `46` <dbl>, `49` <dbl>, `51` <dbl>, `53` <dbl>, `54` <dbl>,
#   `55` <dbl>, `56` <dbl>, `57` <dbl>, `59` <dbl>, `60` <dbl>, `61` <dbl>,
#   `63` <dbl>, `64` <dbl>, `65` <dbl>, `66` <dbl>, `67` <dbl>, `68` <dbl>,
#   `70` <dbl>, `71` <dbl>, `72` <dbl>, `73` <dbl>, `74` <dbl>, `101` <dbl>, …

Source: Sotiriou et al., Breast cancer classification and prognosis based on gene expression profiles from a population-based study, PNAS 100.18 (2003): 10393-10398.

Dataset information

“Sotiriou et al. (2003) described a breast cancer study with 99 women divided into two groups according to their oestrogen receptor status. The ER+ group (65 women) are those women where the cancer has receptors for oestrogen, and the ER− group (34 women) are those without receptors. Out of 7650 variables there are 4404 measured in all 99 samples, and we use these variables for our analysis.”

# Split and convert to matrices for `glmnet`
set.seed(123)  # For reproducibility
test_index <- sample(1:nrow(df), 0.2 * nrow(df))
test <- df[test_index, ]
train_val <- df[-test_index, ]

# Prepare data for glmnet
X <- model.matrix(er ~ ., data = train_val)[, -1]
y <- train_val$er
X_test <- model.matrix(er ~ ., data = test)[, -1]
y_test <- test$er

Source: Bak, Britta Anker and Jens Ledet Jensen, High dimensional classifiers in the imbalanced case, Computational Statistics & Data Analysis 98 (2016): 46-59.

Ridge regression

ridge_model <- glmnet(X, y, family = "binomial", alpha = 0)
plot(ridge_model, xvar="lambda")

Ridge CV (Deviance)

cv_ridge <- cv.glmnet(X, y, family = "binomial", alpha = 0)
plot(cv_ridge)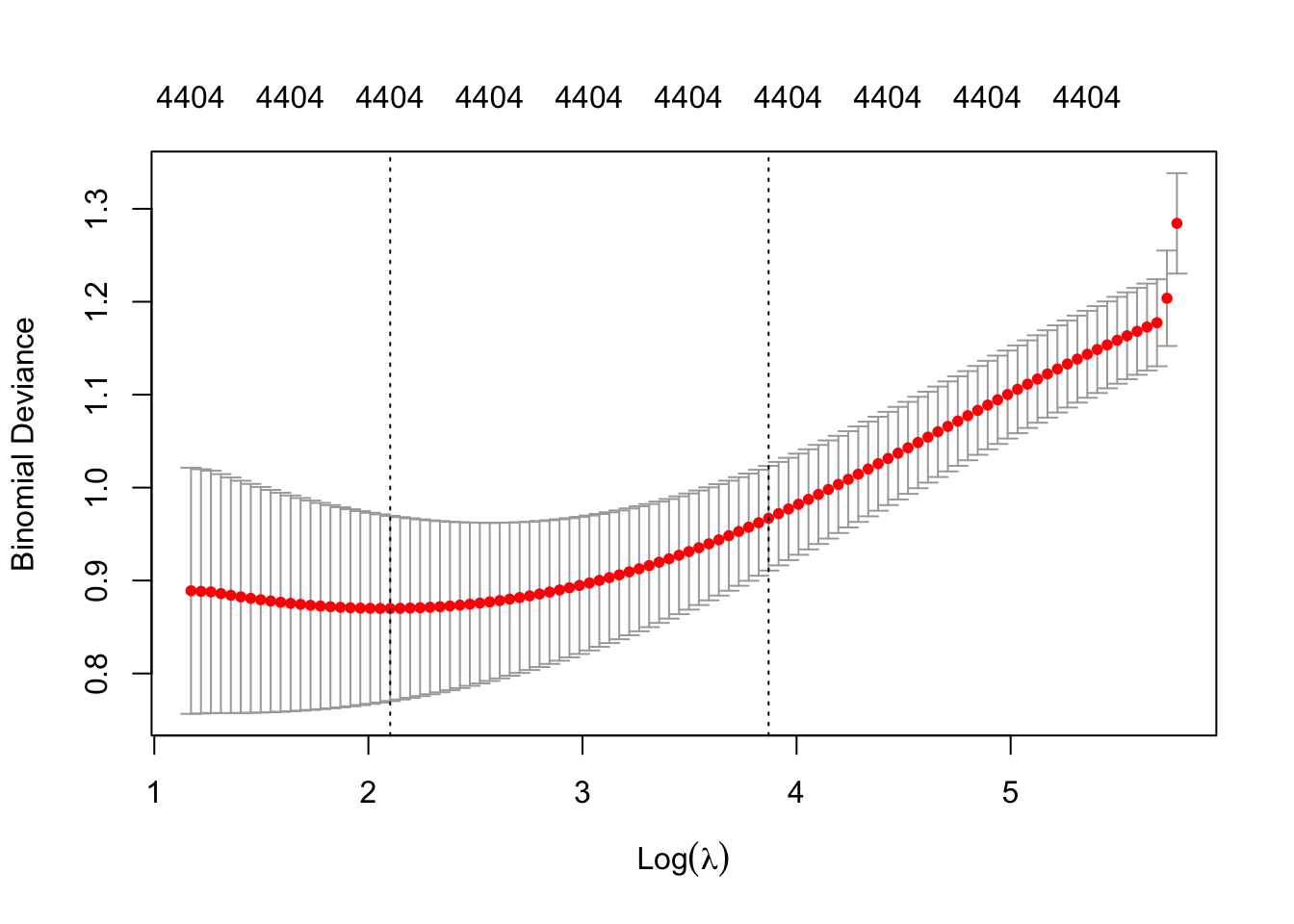

Ridge CV (Classification Error Rate)

cv_ridge <- cv.glmnet(X, y, family = "binomial", alpha = 0, type.measure = "class")
plot(cv_ridge)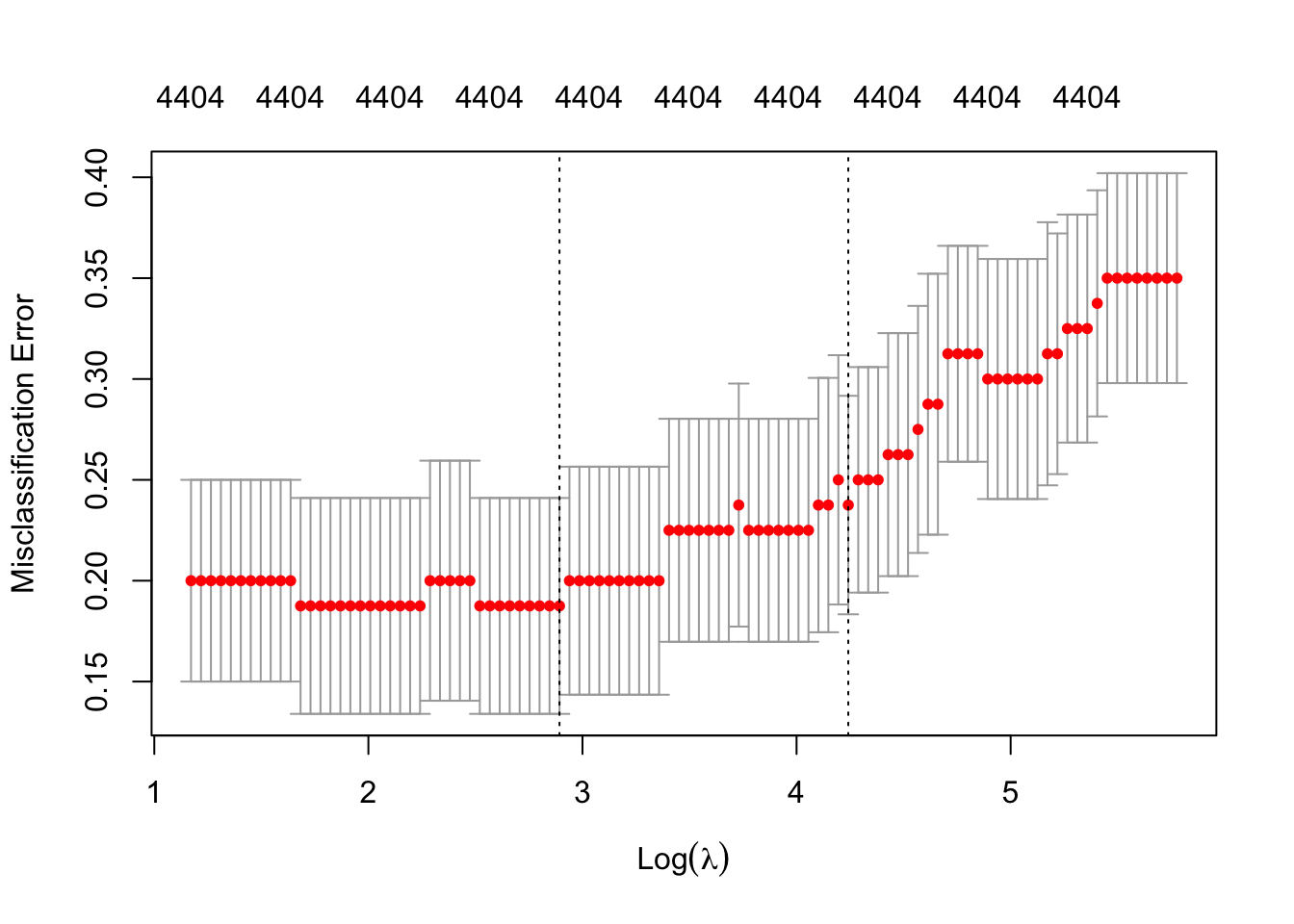

Lasso regression

lasso_model <- glmnet(X, y, family = "binomial", alpha = 1)
plot(lasso_model, xvar="lambda")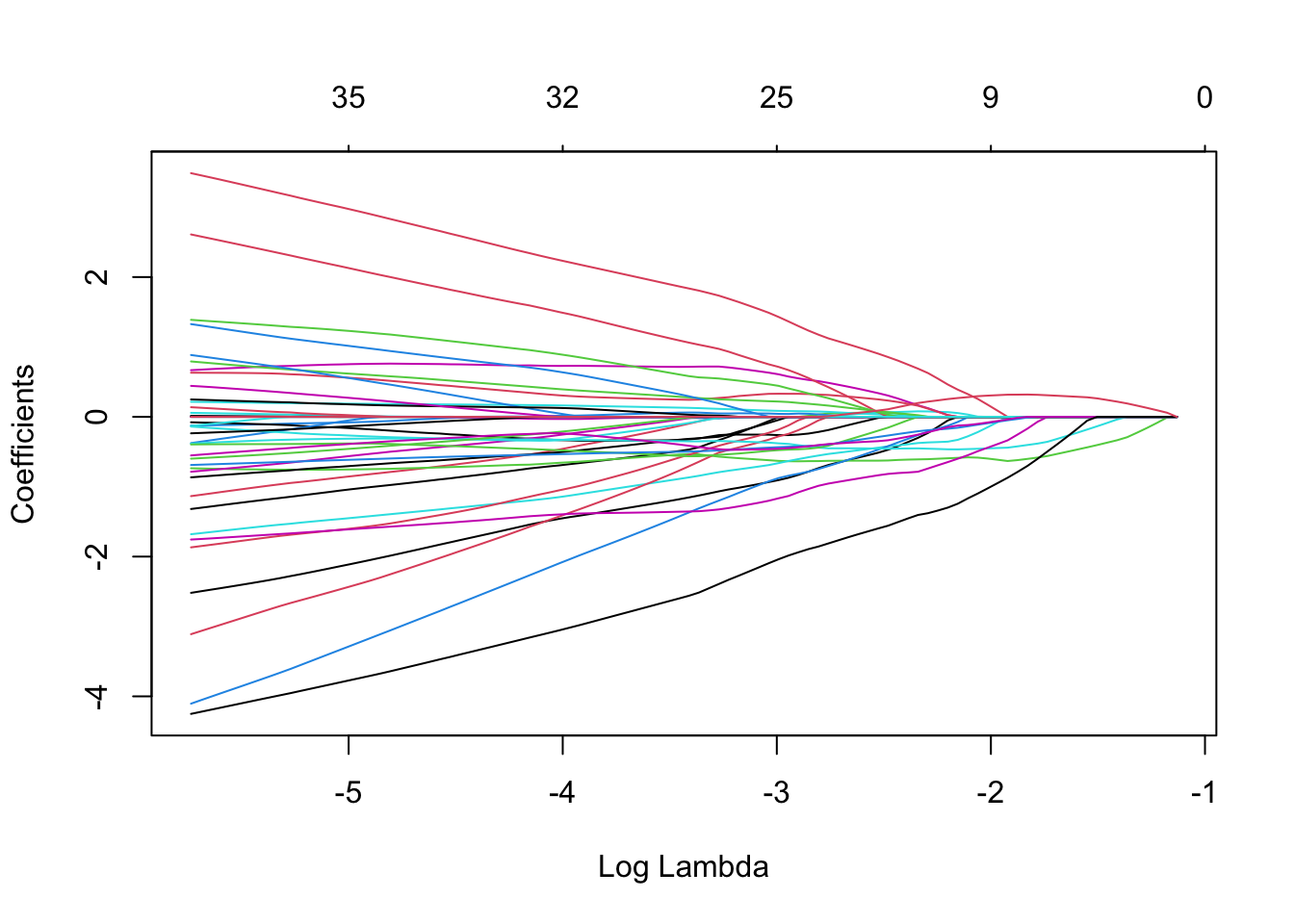

Lasso CV (Deviance)

cv_lasso <- cv.glmnet(X, y, family = "binomial", alpha = 1)
plot(cv_lasso)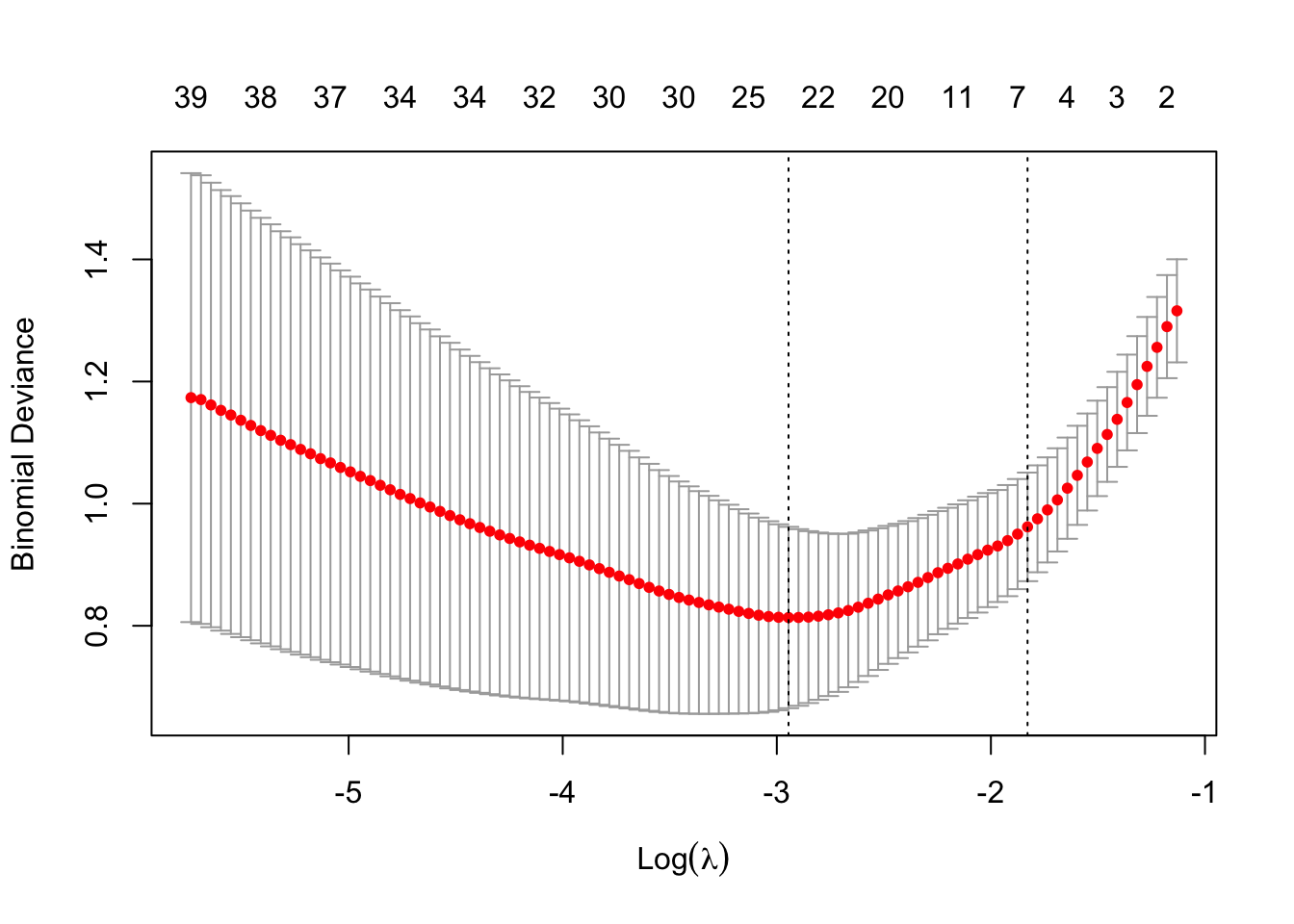

Lasso CV (Classification Error Rate)

cv_lasso <- cv.glmnet(X, y, family = "binomial", alpha = 1, type.measure = "class")
plot(cv_lasso)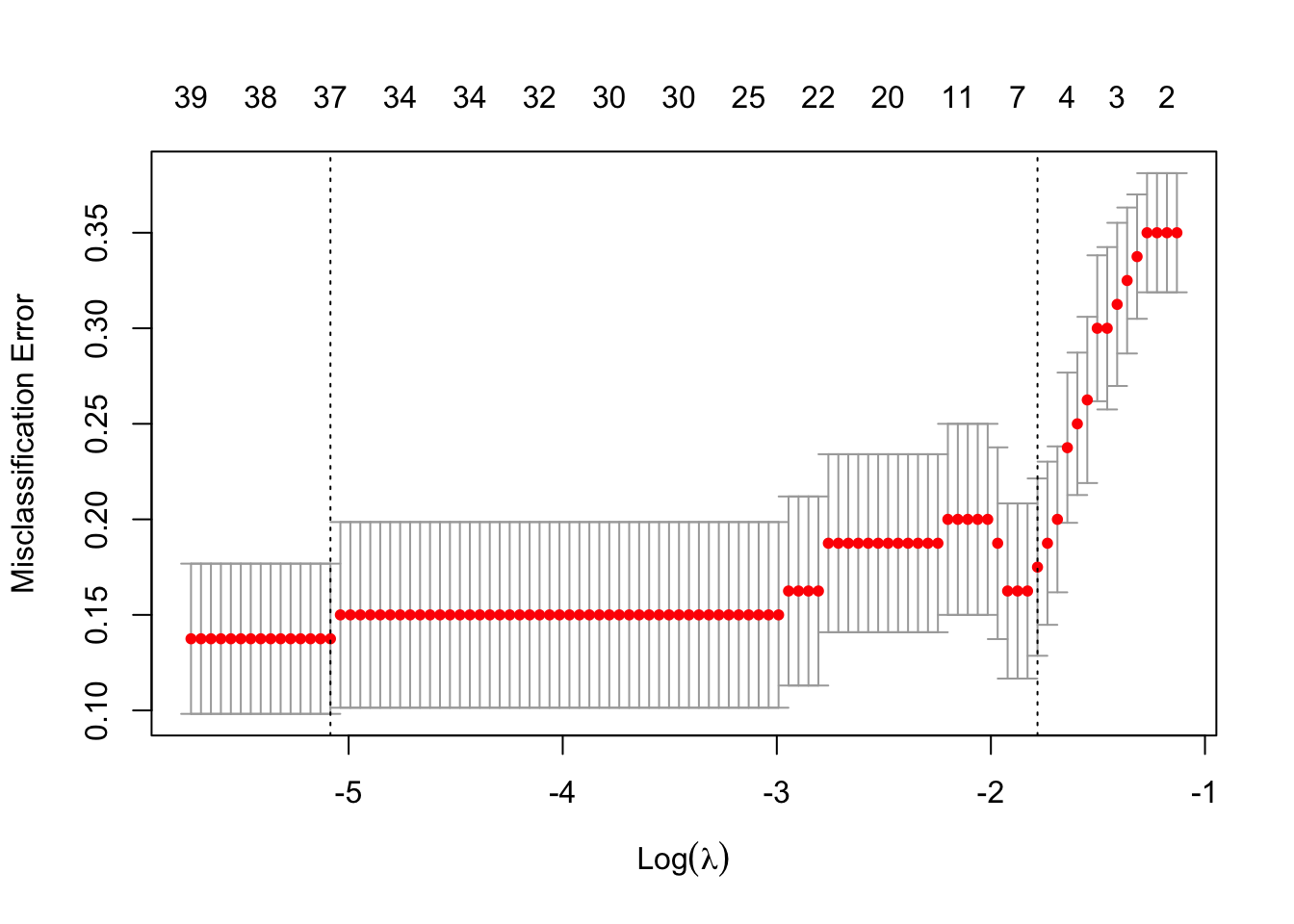

Select a winner & test it

(ridge_cv_error <- min(cv_ridge$cvm))

[1] 0.1875

(lasso_cv_error <- min(cv_lasso$cvm))

[1] 0.1375

sum(coef(cv_lasso, s = "lambda.min") != 0)

[1] 38

sum(coef(cv_lasso, s = "lambda.1se") != 0)

[1] 6

if (ridge_cv_error < lasso_cv_error) {
  best_model <- cv_ridge
  model_type <- "ridge"
} else {
  best_model <- cv_lasso
  model_type <- "lasso"
}

print(paste("Selected model type:", model_type))

[1] "Selected model type: lasso"

y_pred <- predict(best_model, X_test, type = "response", s = "lambda.min") > 0.5
test_accuracy <- mean(y_test == y_pred)
print(paste("Test set accuracy of the selected model:", test_accuracy))

[1] "Test set accuracy of the selected model: 0.842105263157895"

Ridge and Lasso Intuition

Alternate formulation

Ridge regression: minimise MSE subject to \sum_{j=1}^n \beta_j^2 \leq s Lasso regression: minimise MSE subject to \sum_{j=1}^n |\beta_j| \leq s

• Each method is assigns a “budget” to “spend” on the coefficient estimates
• The size of the “budget” is based on \lambda (ridge and lasso)
• This is like Lagrange multipliers (actually look up Karush–Kuhn–Tucker (KKT) conditions)

Ridge vs Lasso: Some intuition

Contours of training MSE against the constraint regions for ridge & lasso.

Lasso leads to a pointier solution space: more likely to set parameters to zero.

Source: James et al. (2021), An Introduction to Statistical Learning, with applications in R, Figure 6.7.

Ridge regression - comments

• Almost all parameters are included, and coefficients are generally low: difficult to interpret model
• Far more efficient than best-subset: only one model for each \lambda needs to be computed, calculating for all \lambda is almost identical to least squares estimates
• Performs better than least-squares where the relationship is linear, but the estimate variance is high

When to use what?

So when should you use elastic net regression, or ridge, lasso, or plain linear regression (i.e., without any regularization)? It is almost always preferable to have at least a little bit of regularization, so generally you should avoid plain linear regression. Ridge is a good default, but if you suspect that only a few features are useful, you should prefer lasso or elastic net because they tend to reduce the useless features’ weights down to zero, as discussed earlier. In general, elastic net is preferred over lasso because lasso may behave erratically when the number of features is greater than the number of training instances or when several features are strongly correlated.

Source: Géron (2022), Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 3rd Edition, Chapter 4.