Show the R package imports
library(tidyverse)library(tidyverse)import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_splitSome of the figures in this presentation are taken from “An Introduction to Statistical Learning, with applications in R” (Springer, 2021) with permission from the authors: G. James, D. Witten, T. Hastie and R. Tibshirani.
Supervised
Unsupervised
\min_{C_1, \dots, C_K} \sum_{k=1}^{K}W(C_k) .
W(C_k) = 2 \sum_{i \in C_k} \sum_{j=1}^{p}(x_{ij} - \bar{x}_{kj})^2 where \bar{x}_{kj} is the mean of feature j for observations in cluster k.
It’s a difficult problem to solve exactly, but the following simple algorithm usually yields a “pretty good solution” (James et al., 2021):
train_df <- read.csv("mnist_train.csv")
train_df# A tibble: 60,000 × 785
X0 X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0 0 0 0
4 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 0 0 0 0 0 0 0 0 0 0
6 0 0 0 0 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0 0 0 0
# ℹ 59,990 more rows
# ℹ 772 more variables: X13 <dbl>, X14 <dbl>, X15 <dbl>, X16 <dbl>, X17 <dbl>,
# X18 <dbl>, X19 <dbl>, X20 <dbl>, X21 <dbl>, X22 <dbl>, X23 <dbl>,
# X24 <dbl>, X25 <dbl>, X26 <dbl>, X27 <dbl>, X28 <dbl>, X29 <dbl>,
# X30 <dbl>, X31 <dbl>, X32 <dbl>, X33 <dbl>, X34 <dbl>, X35 <dbl>,
# X36 <dbl>, X37 <dbl>, X38 <dbl>, X39 <dbl>, X40 <dbl>, X41 <dbl>,
# X42 <dbl>, X43 <dbl>, X44 <dbl>, X45 <dbl>, X46 <dbl>, X47 <dbl>, …train_df = pd.read_csv("mnist_train.csv")
train_df 0 1 2 3 4 5 6 ... 778 779 780 781 782 783 label
0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 5
1 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0
2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 4
3 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 1
4 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 9
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
59995 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 8
59996 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 3
59997 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 5
59998 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 6
59999 0.0 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 8
[60000 rows x 785 columns]Only 19% of the data is non-zero.
# Find the first two '1's in the data, and the first '2'
inds <- c(which(train_df$label == 1)[1:2], which(train_df$label == 2)[1])
obs <- train_df[inds, 480:500]
print(obs) X479 X480 X481 X482 X483 X484 X485 X486 X487
4 0 0 0 0.00000000 0.0000000 0.0000000 0.0000000 0.1882353 0.8666667
7 0 0 0 0.00000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
6 0 0 0 0.01960784 0.5294118 0.9882353 0.9882353 0.7058824 0.0627451
X488 X489 X490 X491 X492 X493 X494
4 0.9843137 0.98431370 0.6745098 0.0000000 0.0000000 0.0000000 0.0000000
7 0.0000000 0.99215686 0.9882353 0.9882353 0.9882353 0.1647059 0.0000000
6 0.0000000 0.08235294 0.7960784 0.9921569 0.9686274 0.5058824 0.6784314
X495 X496 X497 X498 X499
4 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
7 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
6 0.9882353 0.9882353 0.7215686 0.2588235 0.1921569
Take just a fraction of the data, and make a plotting function.
# Separate the features and the labels
x <- as.matrix(train_df[, -785])
y <- train_df$label
# Split the data into train/validation and test sets
set.seed(88)
test_indices <- sample(1:nrow(x),
size = 0.2*nrow(x))
x_test <- x[test_indices,]
y_test <- y[test_indices]
x_train_val <- x[-test_indices,]
y_train_val <- y[-test_indices]
train_indices <- sample(1:nrow(x_train_val),
size = 0.75*nrow(x_train_val))
x_train <- x_train_val[train_indices,]
y_train <- y_train_val[train_indices]
x_val <- x_train_val[-train_indices,]
y_val <- y_train_val[-train_indices]# Plot a single digit
plot_digit <- function(digit) {
digit_matrix <- matrix(digit,
nrow = 28, byrow = TRUE)
digit_matrix <- t(digit_matrix)
digit_matrix <- 1 - digit_matrix[,28:1]
image(1:28, 1:28, digit_matrix,
col = gray((0:255)/255),
xaxt = 'n', yaxt = 'n')
}# Convert to NumPy arrays
train_df = pd.read_csv("mnist_train.csv")
x = train_df.iloc[:, :-1].to_numpy()
y = train_df.iloc[:, -1].to_numpy().flatten()
# Split the data into train/validation and test sets
x_train_val, x_test, y_train_val, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
x_train, x_val, y_train, y_val = train_test_split(x_train_val, y_train_val, test_size=0.25, random_state=0)
x_train = x_train[:1000]
y_train = y_train[:1000]
# Plot a single digit
def plot_digit(digit, ax):
digit_matrix = 1 - digit.reshape((28, 28))
ax.imshow(digit_matrix, cmap='gray',
vmin=0, vmax = 1,
interpolation='none')
ax.set_xticks([])
ax.set_yticks([]) plot_digit(x_train[1,])
fig, ax = plt.subplots(figsize=(4,4))
plot_digit(x_train[0, :], ax)
par(mfrow = c(2,5))
for (i in 1:10) {
plot_digit(x_train[i,])
title(y_train[i])
}
fig, axes = plt.subplots(2, 5, figsize=(10, 5))
fig.subplots_adjust(wspace=0.5, hspace=0.5)
for i, ax in enumerate(axes.ravel()):
plot_digit(x_train[i, :], ax)
ax.set_title(y_train[i])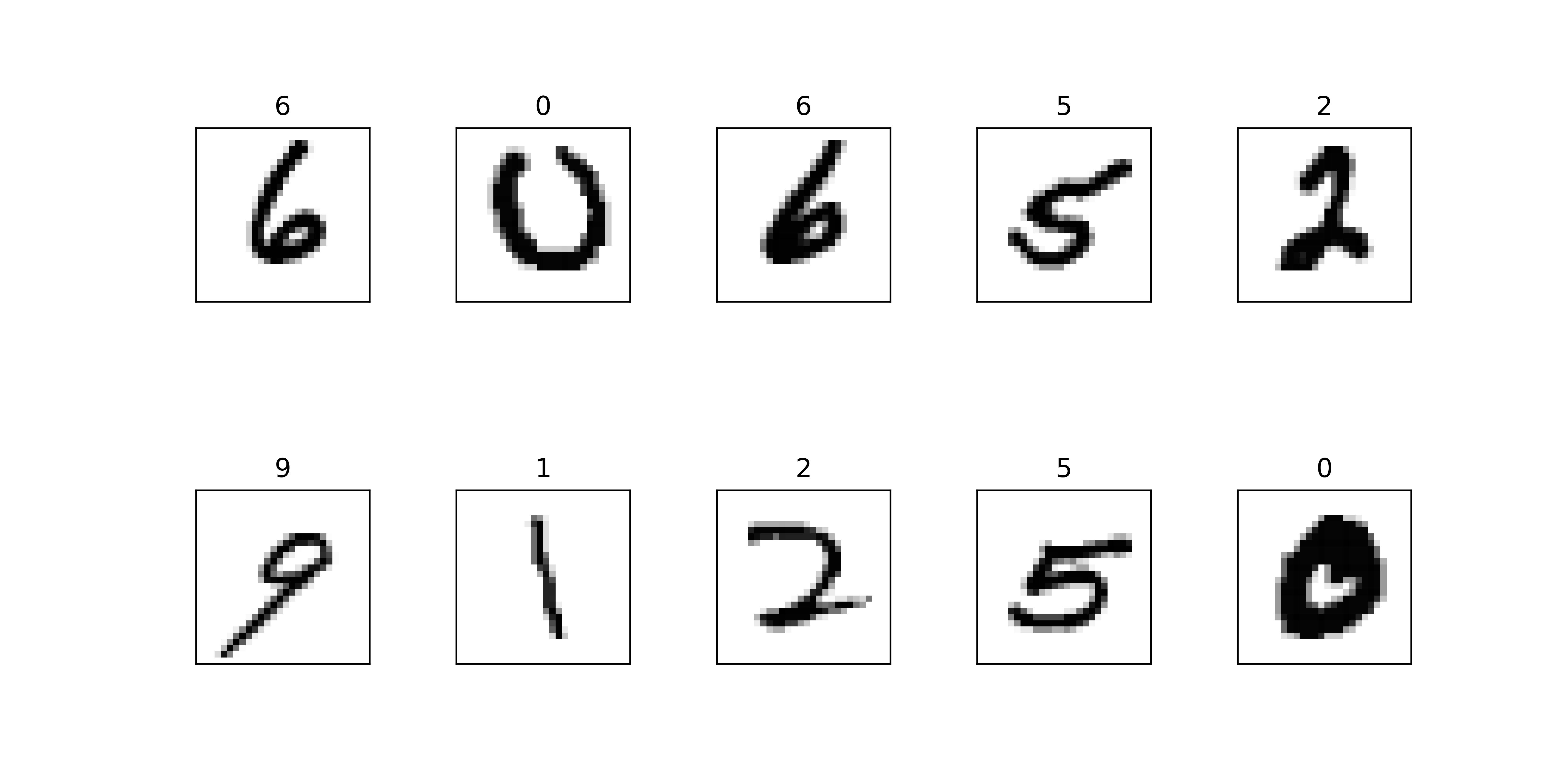
# Plot one of each digit
par(mfrow = c(2,5))
for (i in 0:9) {
plot_digit(x_train[y_train == i,][1,])
title(i)
}
set.seed(1)
kmeans_out <- kmeans(x_train, centers = 10)# Plot the cluster centers
par(mfrow = c(2,5))
for (i in 1:10) {
plot_digit(kmeans_out$centers[i,])
}
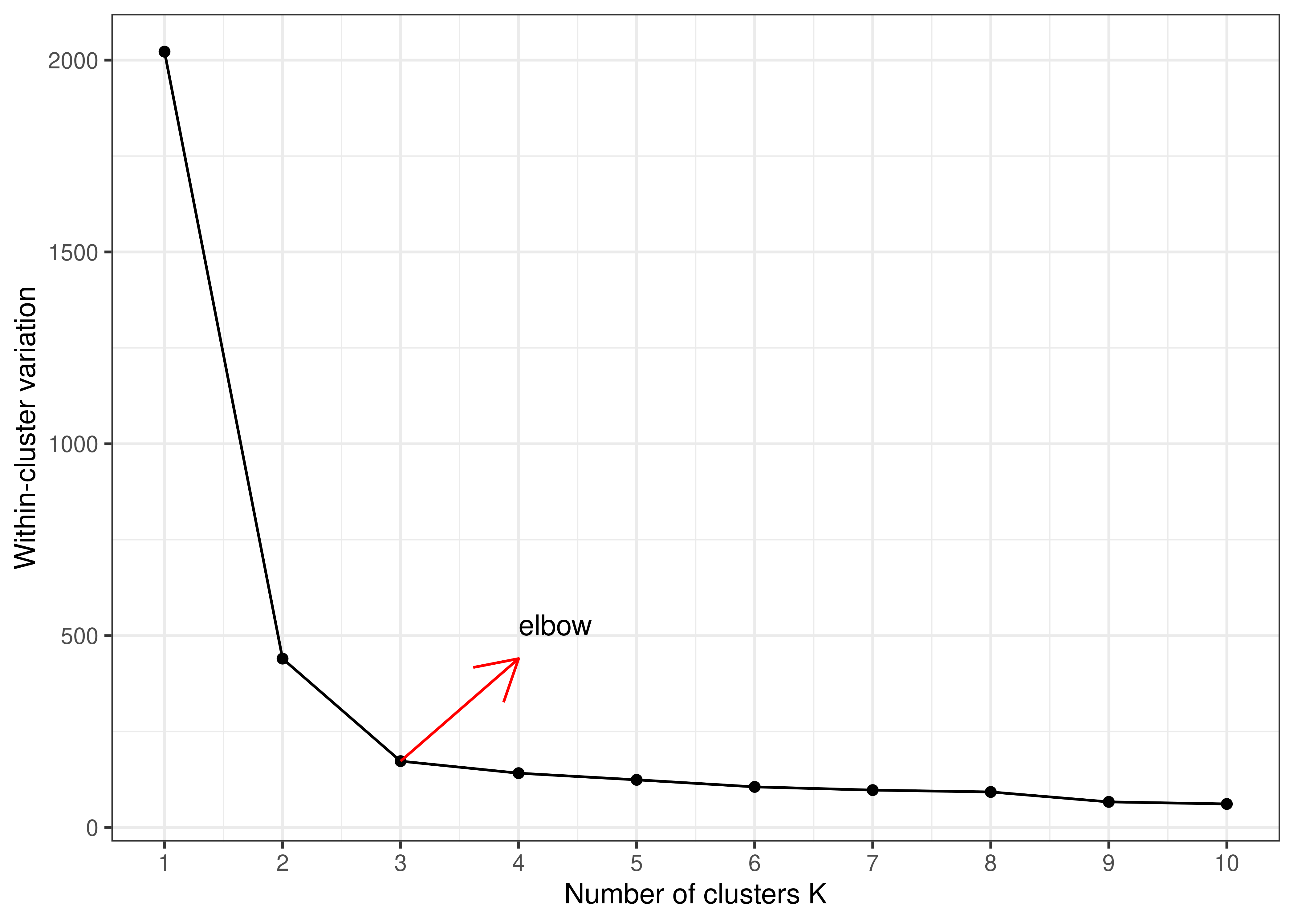
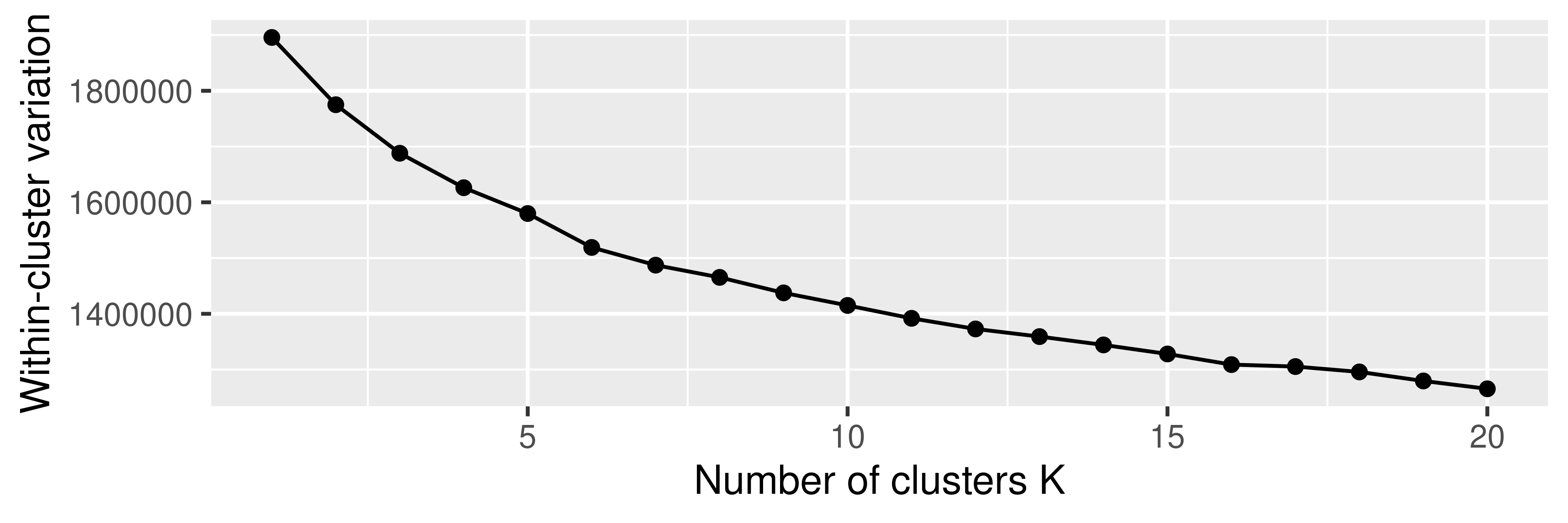
The within-cluster variation is
kmeans_out$tot.withinss[1] 1413762set.seed(2)
kmeans_out <- kmeans(x_train, centers = 10)# Plot the cluster centers
par(mfrow = c(2,5))
for (i in 1:10) {
plot_digit(kmeans_out$centers[i,])
}
The within-cluster variation is
kmeans_out$tot.withinss[1] 1410923set.seed(3)
kmeans_out <- kmeans(x_train, centers = 10)# Plot the cluster centers
par(mfrow = c(2,5))
for (i in 1:10) {
plot_digit(kmeans_out$centers[i,])
}
The within-cluster variation is
kmeans_out$tot.withinss[1] 1410441wss <- rep(0, 20)
for (k in 1:20) {
kmeans_out <- kmeans(x_train, centers = k)
wss[k] <- kmeans_out$tot.withinss
}data.frame(k = 1:20, wss = wss) %>%
ggplot(aes(x = k, y = wss)) +
geom_line() +
geom_point() +
labs(x = 'Number of clusters K', y = 'Within-cluster variation')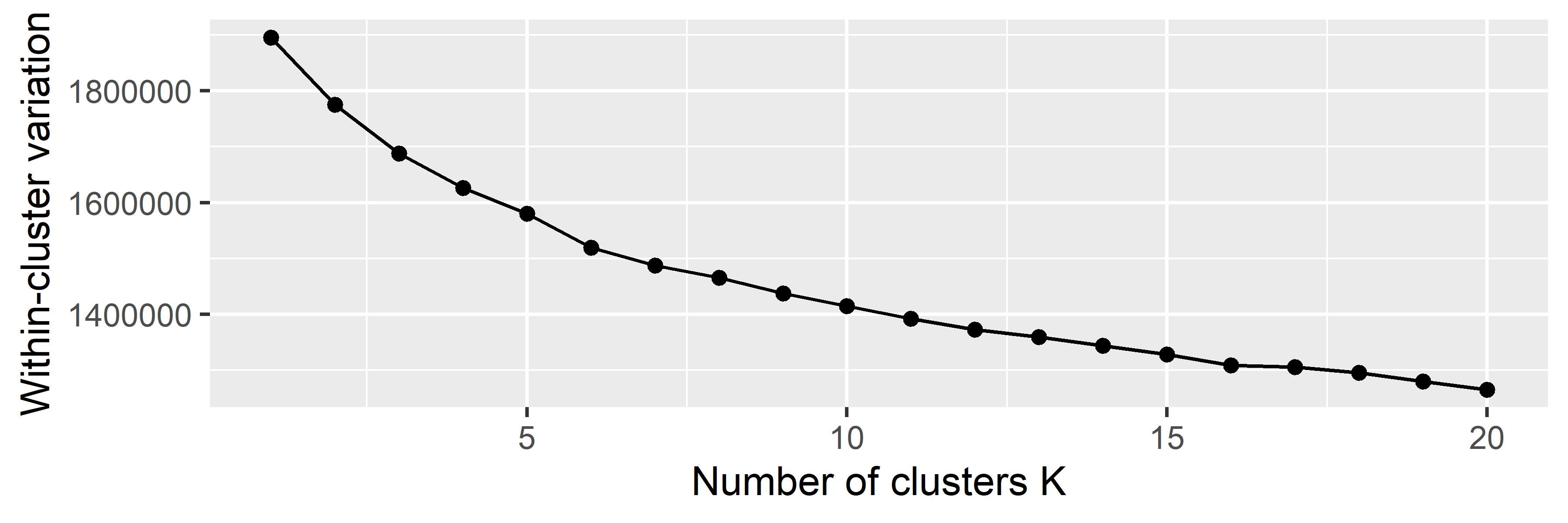
wss = np.zeros(20)
for k in range(1, 21):
kmeans = KMeans(n_clusters=k)
kmeans.fit(x_train);
wss[k - 1] = kmeans.inertia_KMeans(n_clusters=20)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KMeans(n_clusters=20)
plt.plot(range(1, 21), wss, marker='o', linestyle='-', mfc = 'none', color = 'black', markersize=8)
plt.xlabel('Number of clusters K')
plt.ylabel('Within-cluster variation')
plt.xticks(np.arange(5, 21, step=5));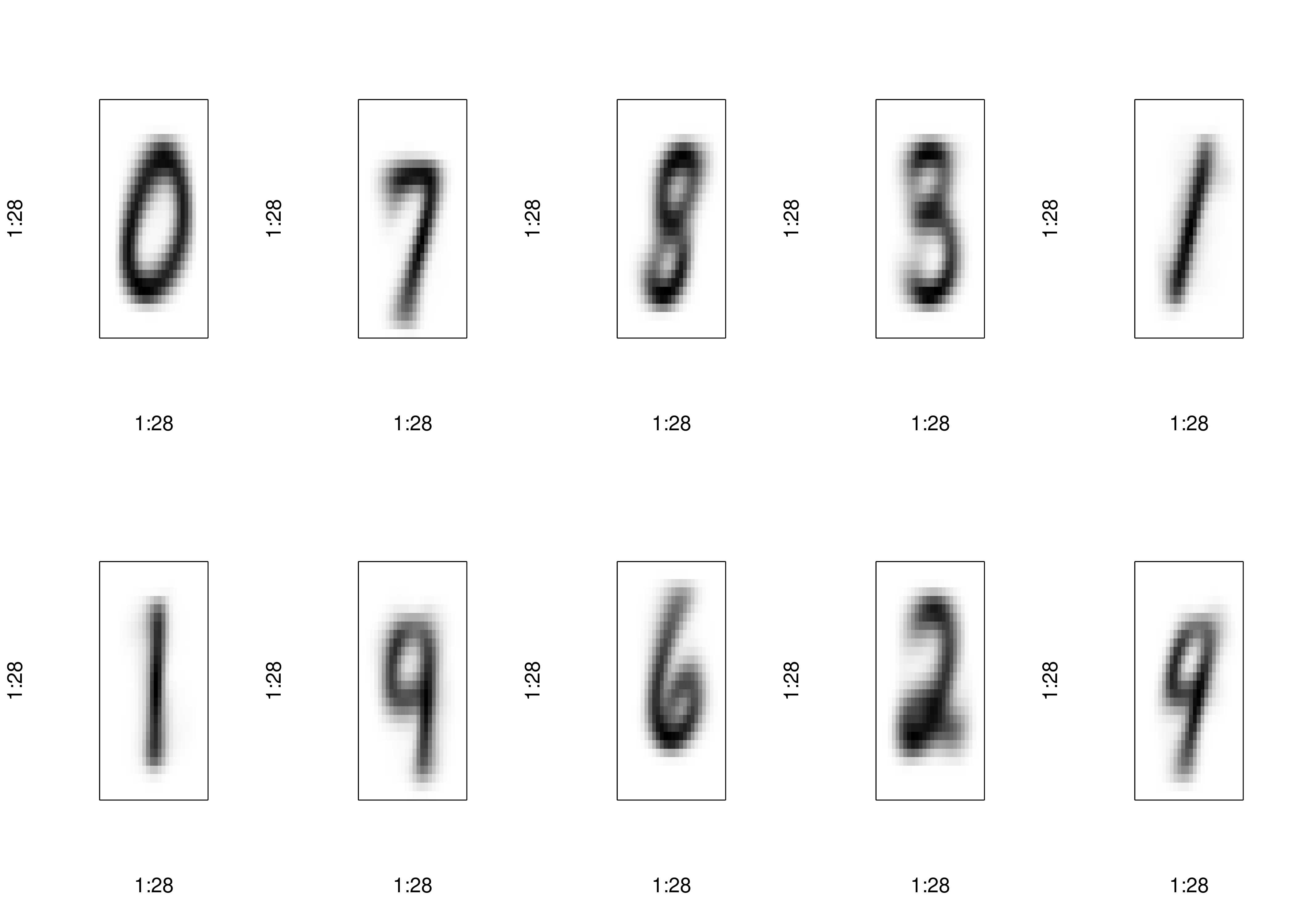
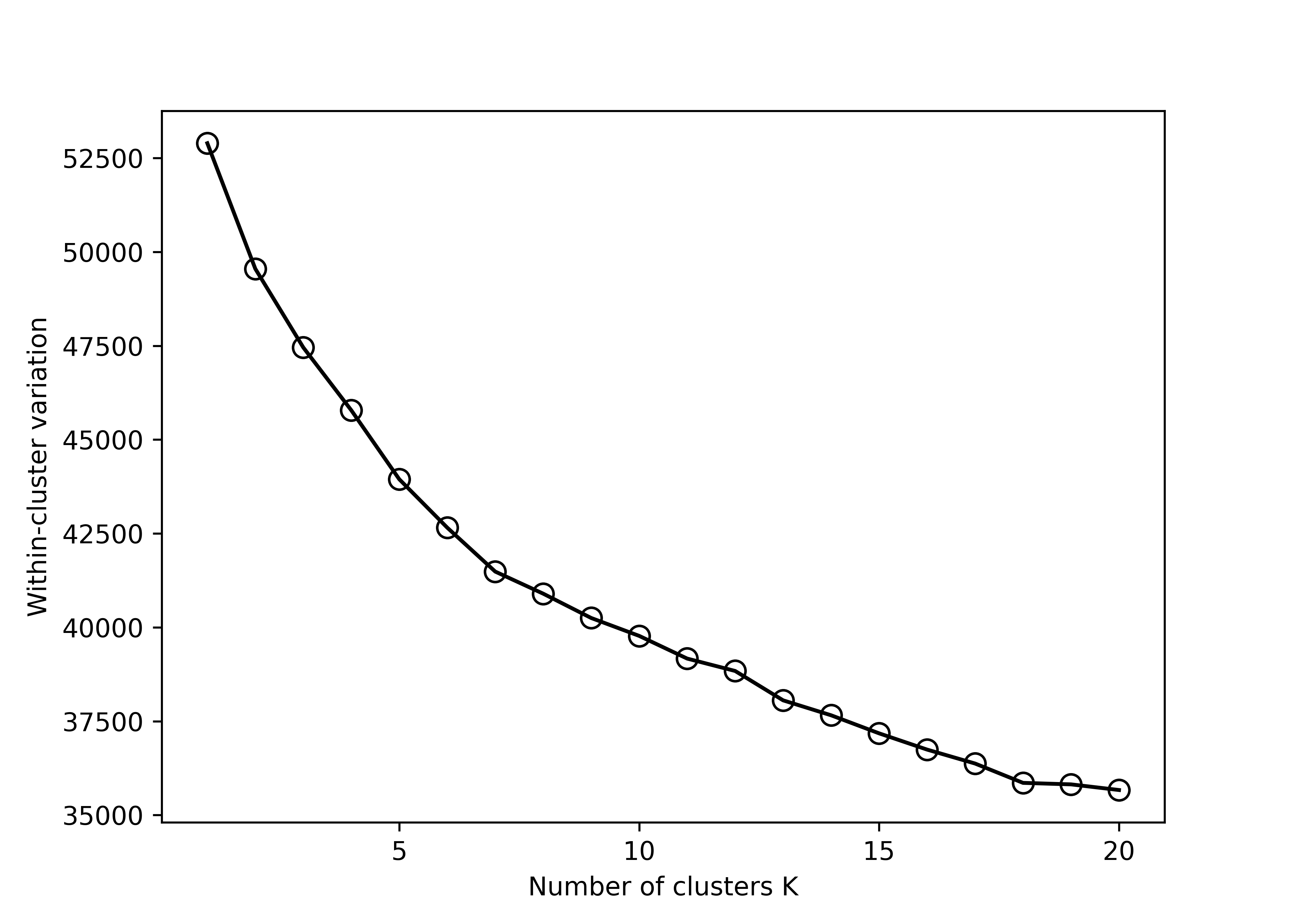
wss <- rep(0, 200)
x_tiny_subset <- x_train[1:1000,]
for (k in 1:200) {
kmeans_out <- kmeans(x_tiny_subset, centers = k)
wss[k] <- kmeans_out$tot.withinss
}data.frame(k = 1:200, wss = wss) %>%
ggplot(aes(x = k, y = wss)) +
geom_line() +
geom_point() +
labs(x = 'Number of clusters K', y = 'Within-cluster variation')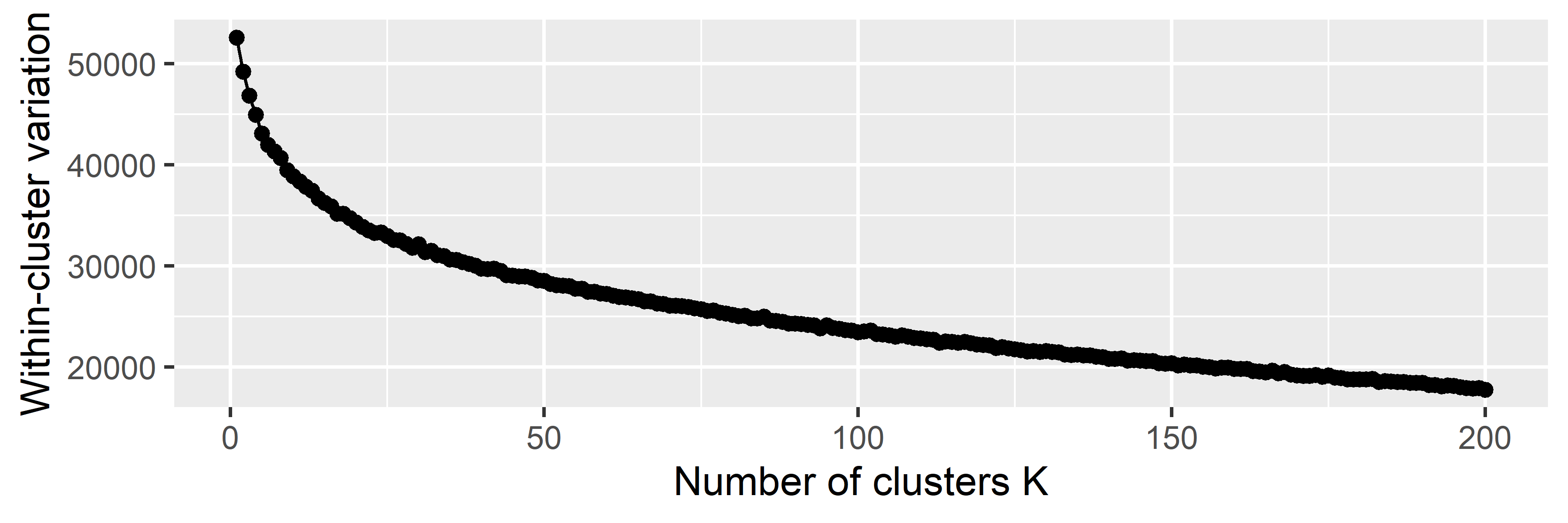
wss = np.zeros(200)
x_tiny_subset = x_train[:1000]
for k in range(1, 201):
kmeans = KMeans(n_clusters=k)
kmeans.fit(x_tiny_subset);
wss[k - 1] = kmeans.inertia_KMeans(n_clusters=200)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
KMeans(n_clusters=200)
plt.plot(range(1, 201), wss, marker='o', linestyle='-', mfc = 'none', color='black')
plt.xlabel('Number of clusters K')
plt.ylabel('Within-cluster variation')
plt.xticks(np.arange(0, 201, step=50));
plt.show()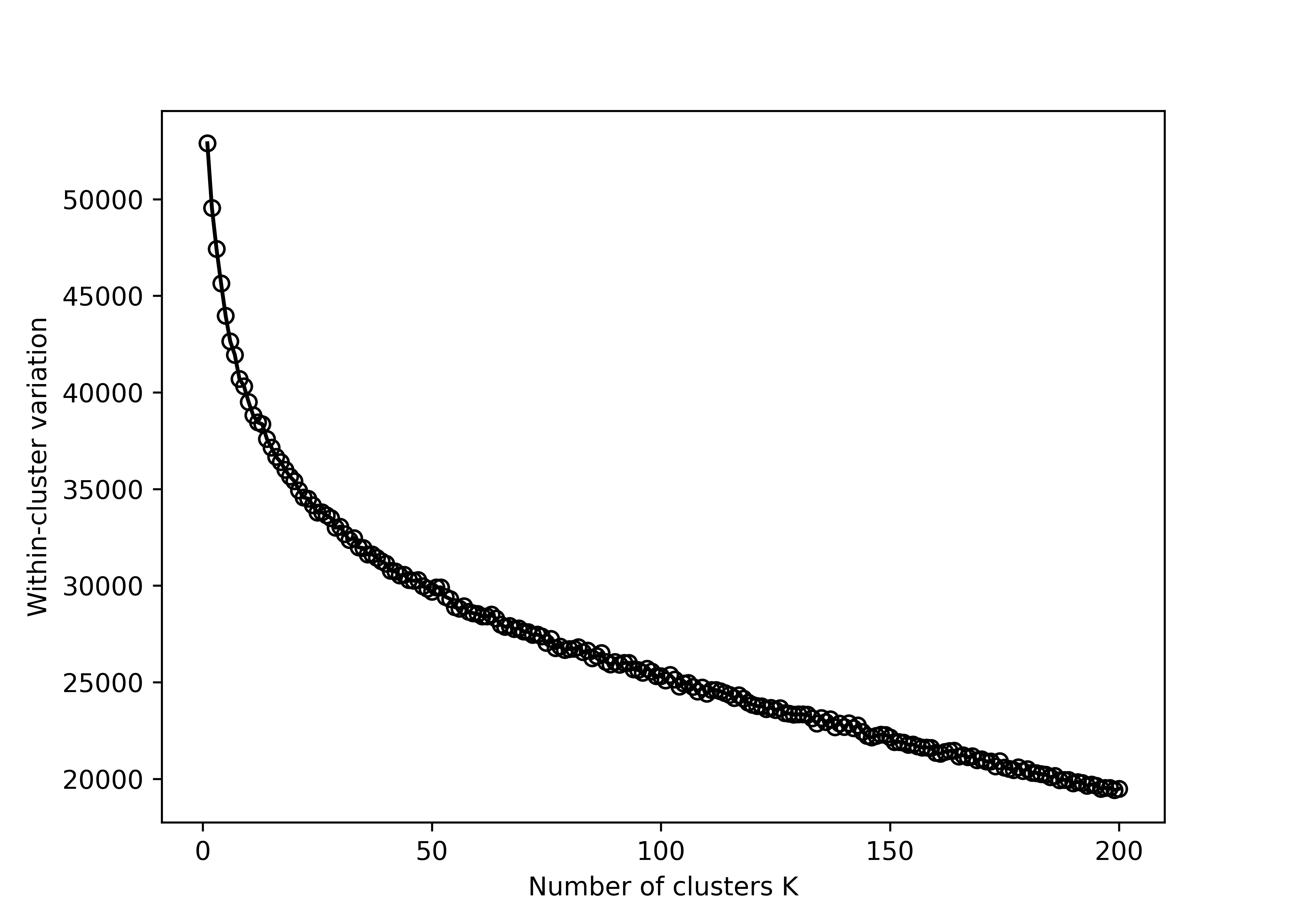
Algorithm:
Example of agglomerative clustering (with single linkage).
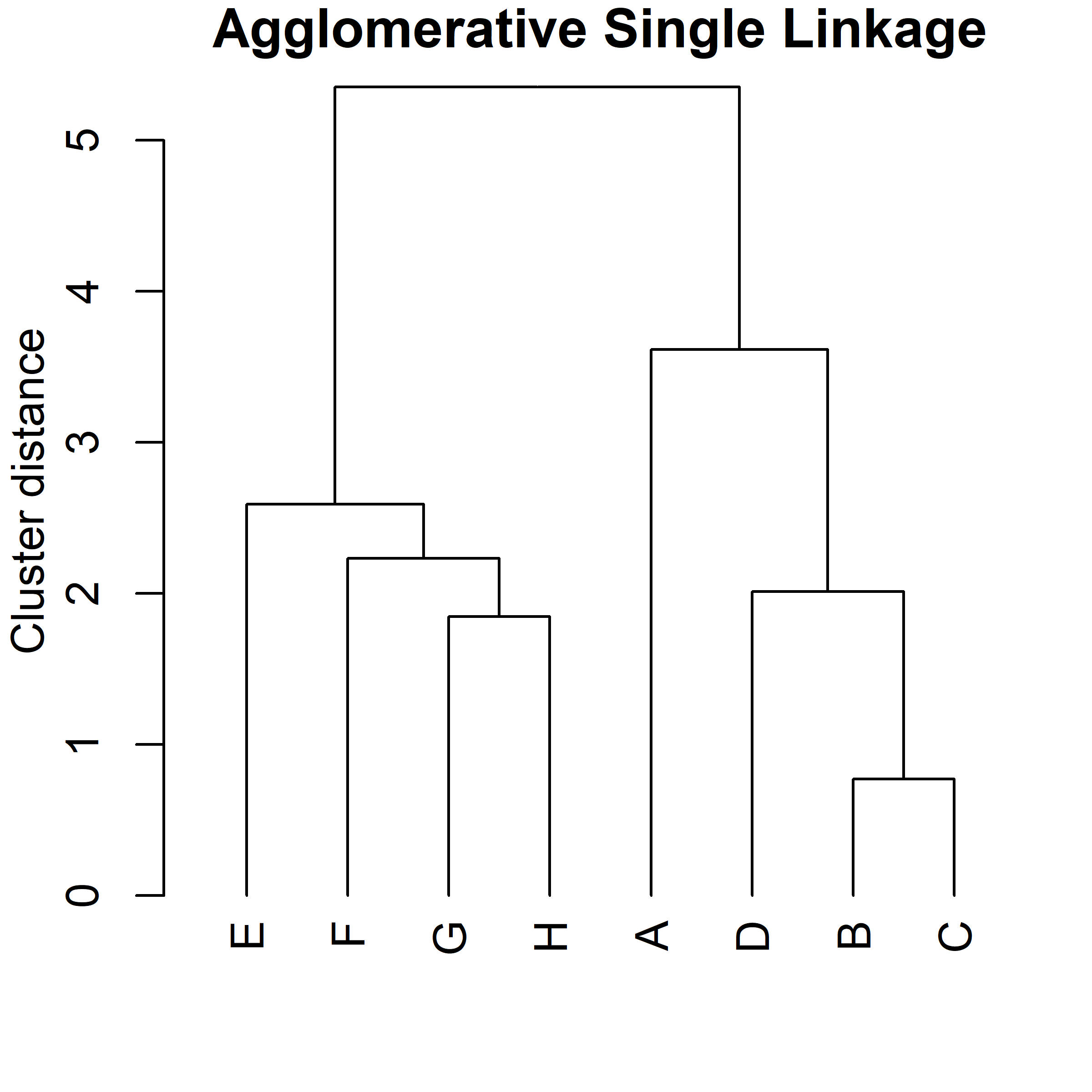
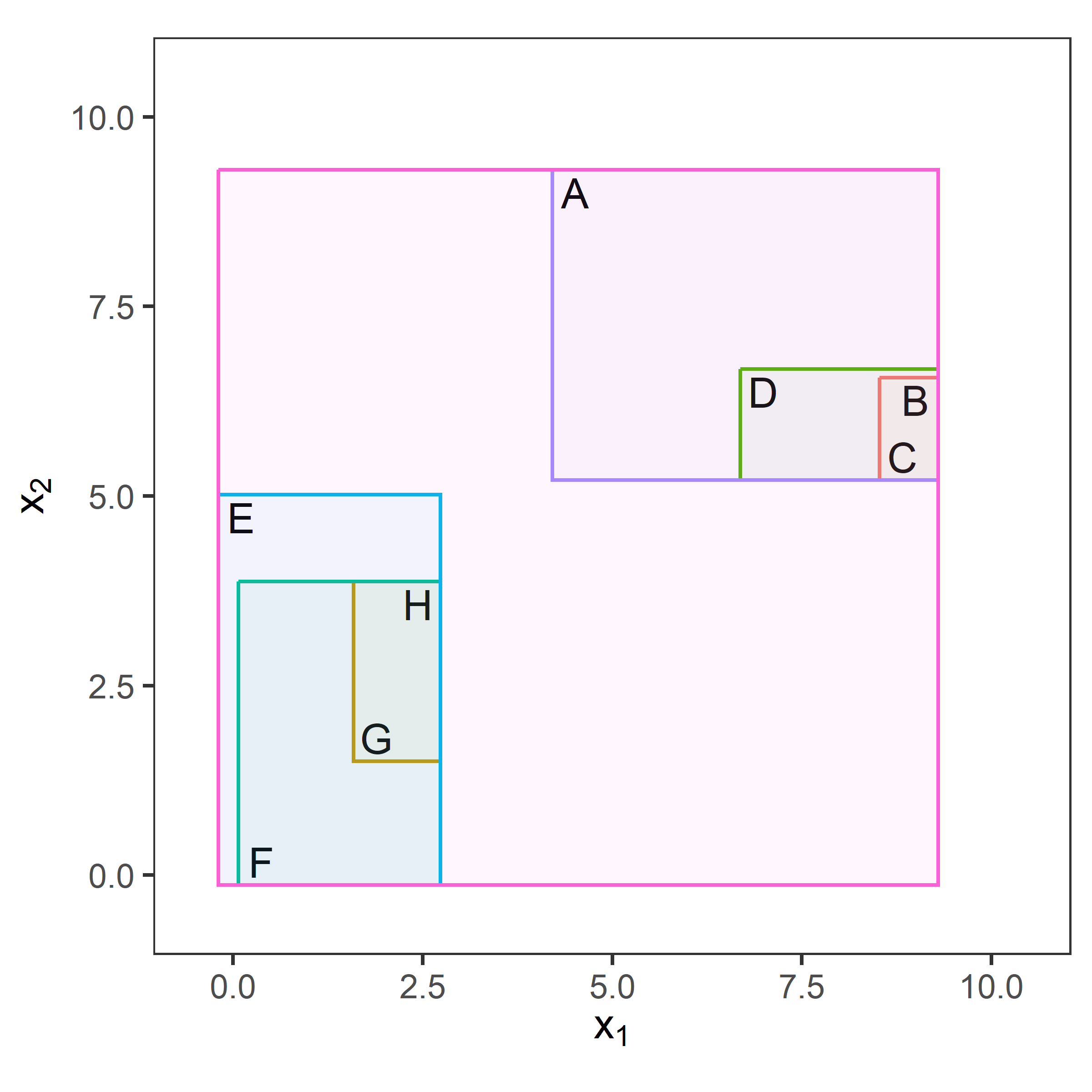
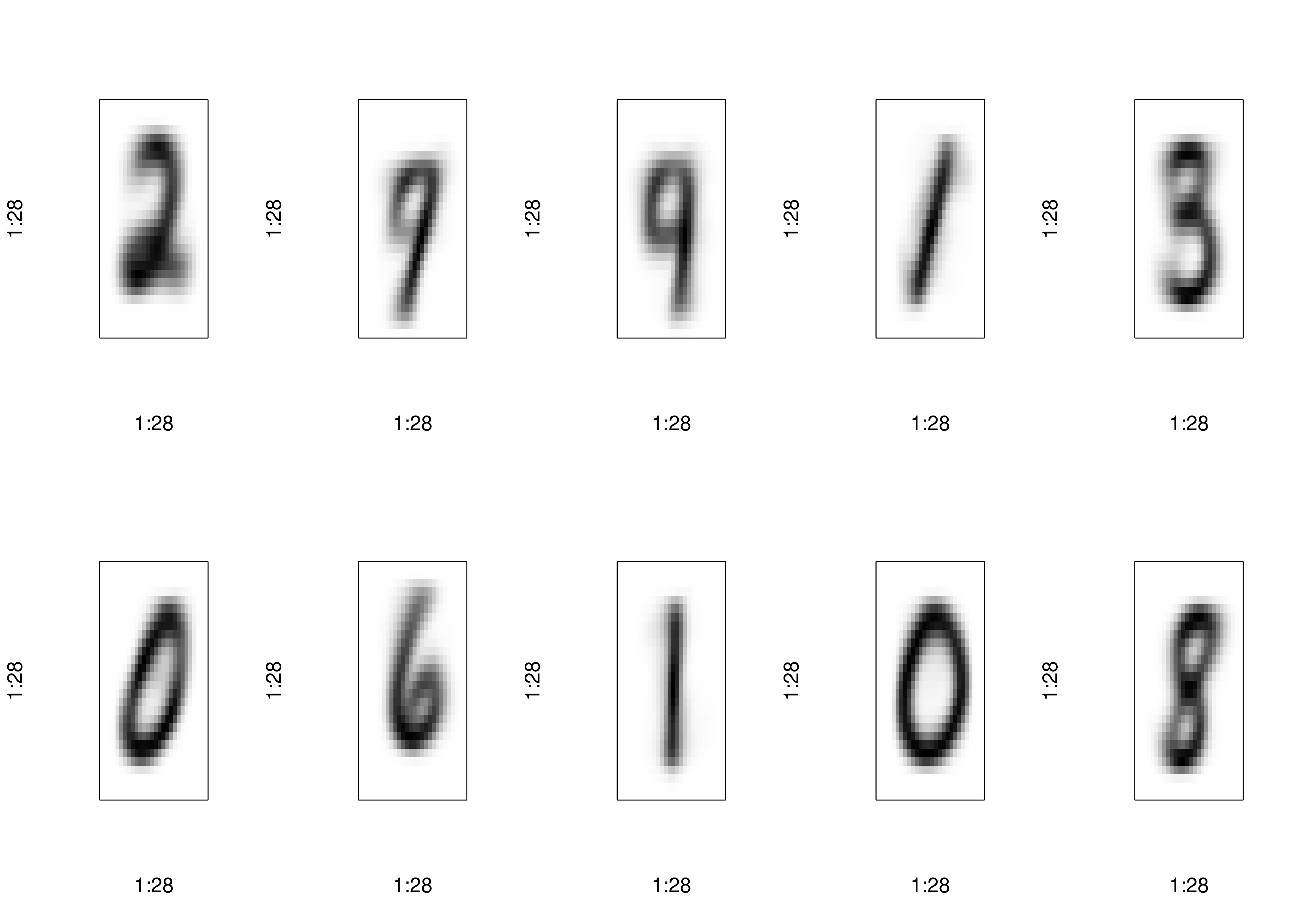
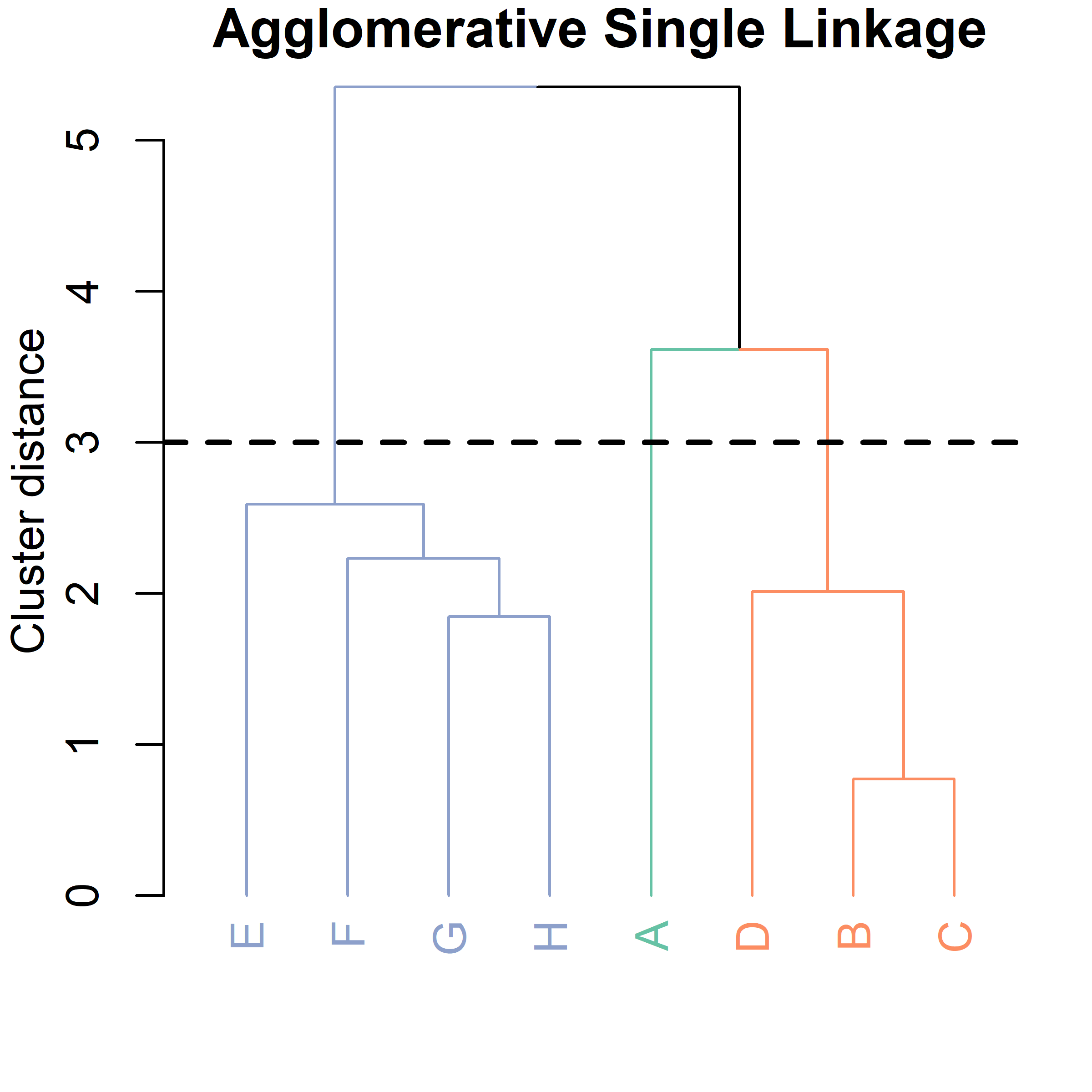
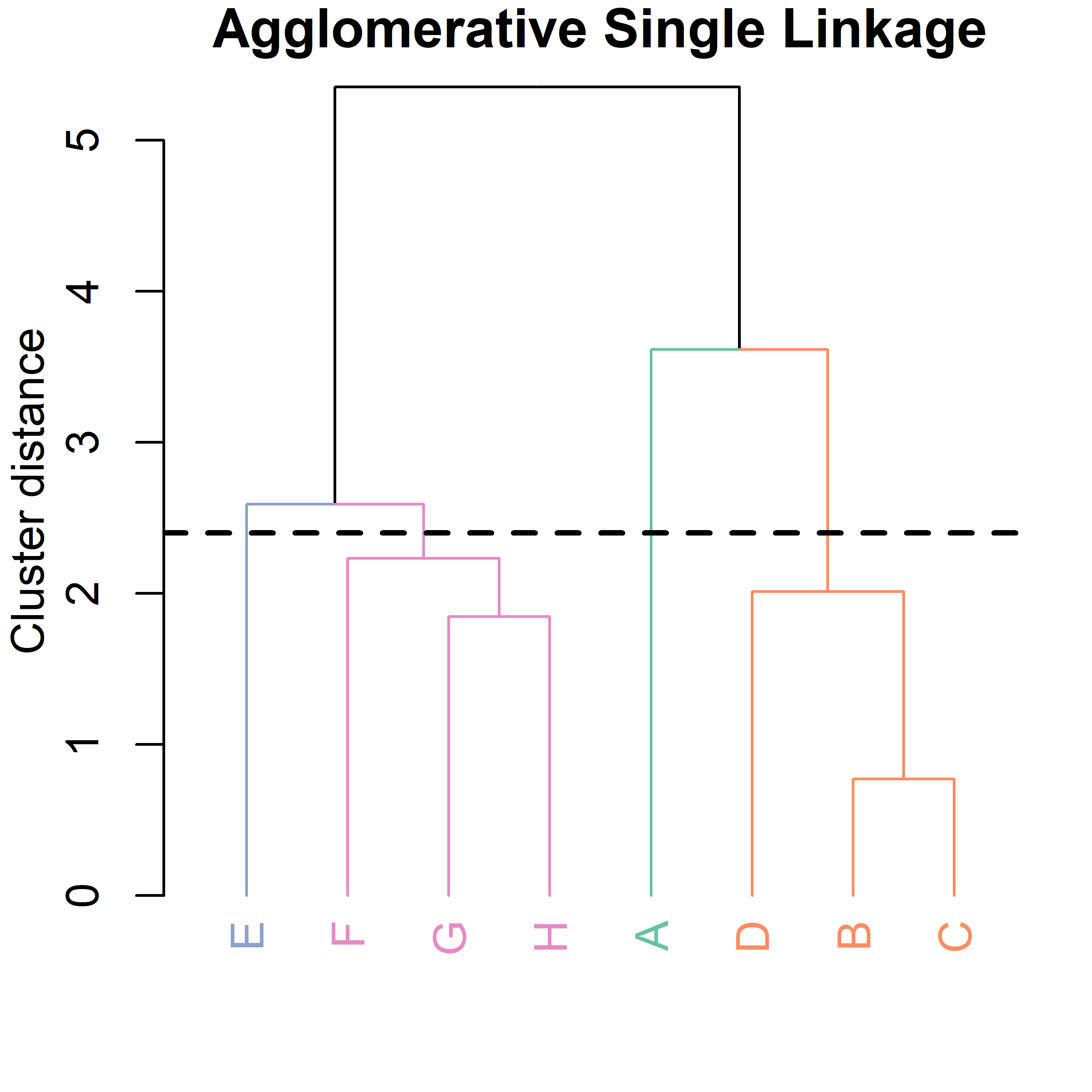
Now, we also need a way to compute the dissimilarity between clusters with more than one data point.
“… our brains are sort of bad at looking at columns of numbers, but absolutely ace at locating patterns and information in a two-dimensional field of vision” Jordan Ellenberg
set.seed(2)
x1 <- 1:10
x2 <- 1:10 + runif(n = 10)*4
dataPCA <- data.frame(x1 = x1 - mean(x1), x2 = x2 - mean(x2), col = factor(1:10))
# Plot simple PCA
PCA0 <- ggplot(dataPCA) + geom_point(aes(x = x1, y = x2, colour = col),
shape = 16, size = 3) +
theme_bw() +
theme(axis.text=element_blank(),
axis.ticks=element_blank(),
legend.position = "none",
panel.border = element_blank(),
panel.grid = element_blank(),
axis.line = element_line(arrow = arrow())) +
coord_equal() +
labs(x = expression("Math Skill - " * X[1]), y = expression("Math Enjoyment - " * X[2])) +
xlim(-6,6) + ylim(-6,6)
PCA0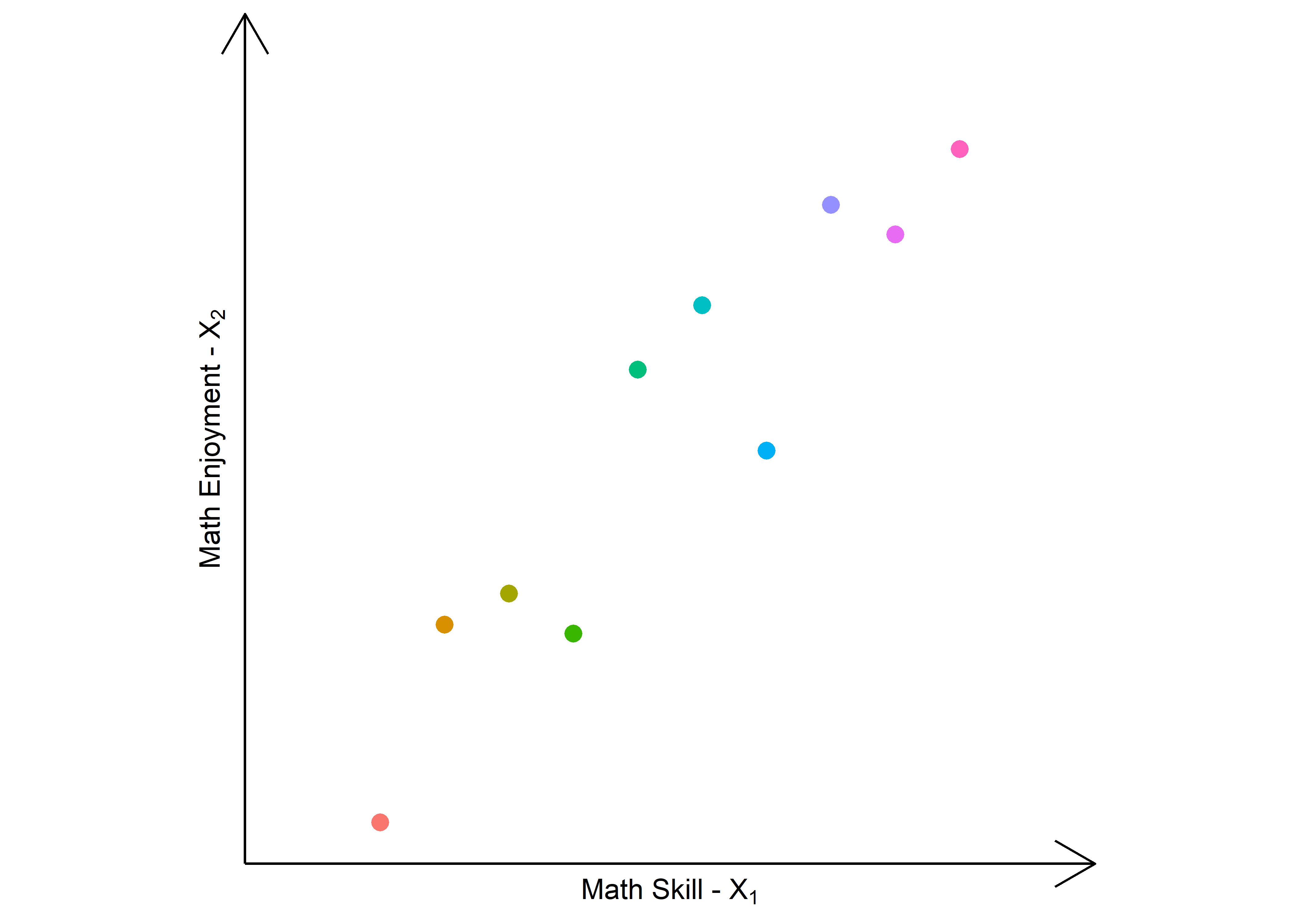
pca.out <- prcomp(dataPCA[, 1:2])
PCA1 <- PCA0 + geom_segment(x=pca.out$rotation[1,1]*-8,
y=pca.out$rotation[2,1]* -8,
xend=pca.out$rotation[1,1]*8,
yend=pca.out$rotation[2,1]*8, linewidth = 1.2,
arrow = arrow())
PCA1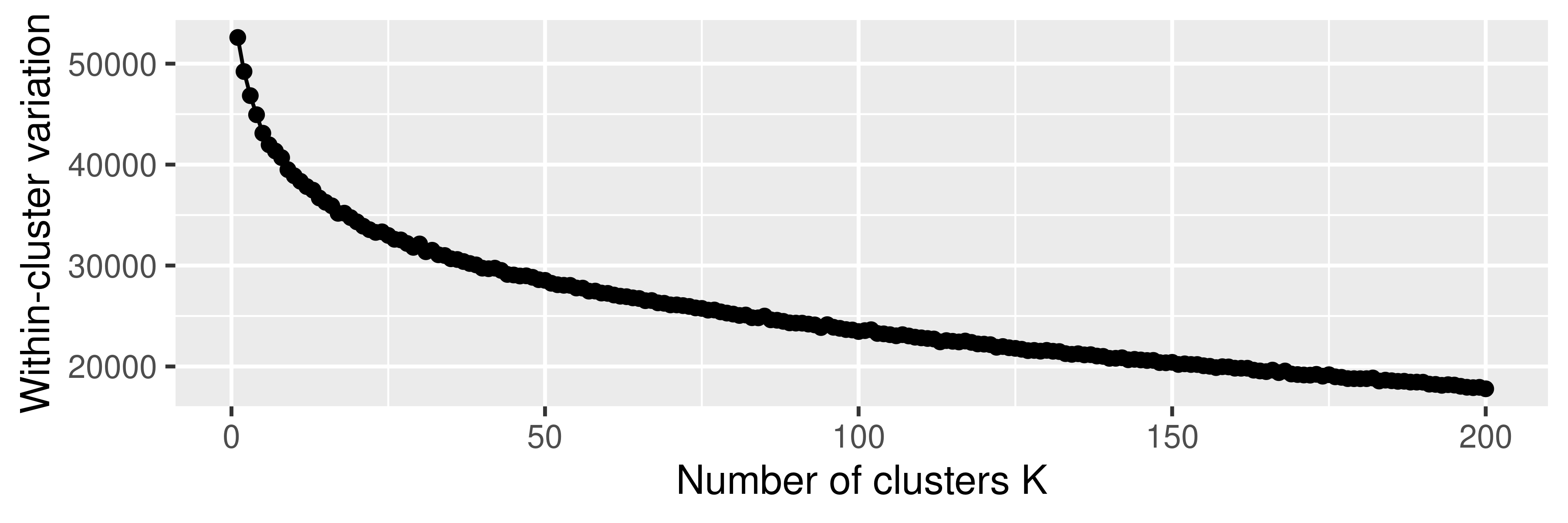
dataPCA <- dataPCA %>% mutate(z1 = pca.out$x[,1],
z2 = pca.out$x[,2],
proj1 = z1/sqrt(pca.out$rotation[1,1]^2 +
pca.out$rotation[2,1]^2)*pca.out$rotation[1,1],
proj2 = z1/sqrt(pca.out$rotation[1,1]^2 +
pca.out$rotation[2,1]^2)*pca.out$rotation[2,1])
(PCA2 <- PCA1 + geom_segment(data = dataPCA, aes(x = proj1, y= proj2, xend = x1, yend = x2)))
PROJ1 <- ggplot(dataPCA) + geom_point(aes(x = z1, y = 1, colour = col),
shape = 16, size = 3) +
theme_bw() +
theme(axis.text=element_blank(),
axis.ticks=element_blank(),
legend.position = "none",
panel.border = element_blank(),
panel.grid = element_blank(),
axis.line.x = element_line(arrow = arrow()),
axis.line.y = element_line(arrow = arrow(), colour = "white"),
axis.title.y = element_text(colour = "white")) +
coord_equal() +
labs(x = expression("Math Nerdiness - " * Z[1]), y = "asfdasf") +
ylim(0.5,1.5) + xlim(-1 -6*(pca.out$rotation[1,1] + pca.out$rotation[2,1]),
6*(pca.out$rotation[1,1] + pca.out$rotation[2,1]))
PROJ1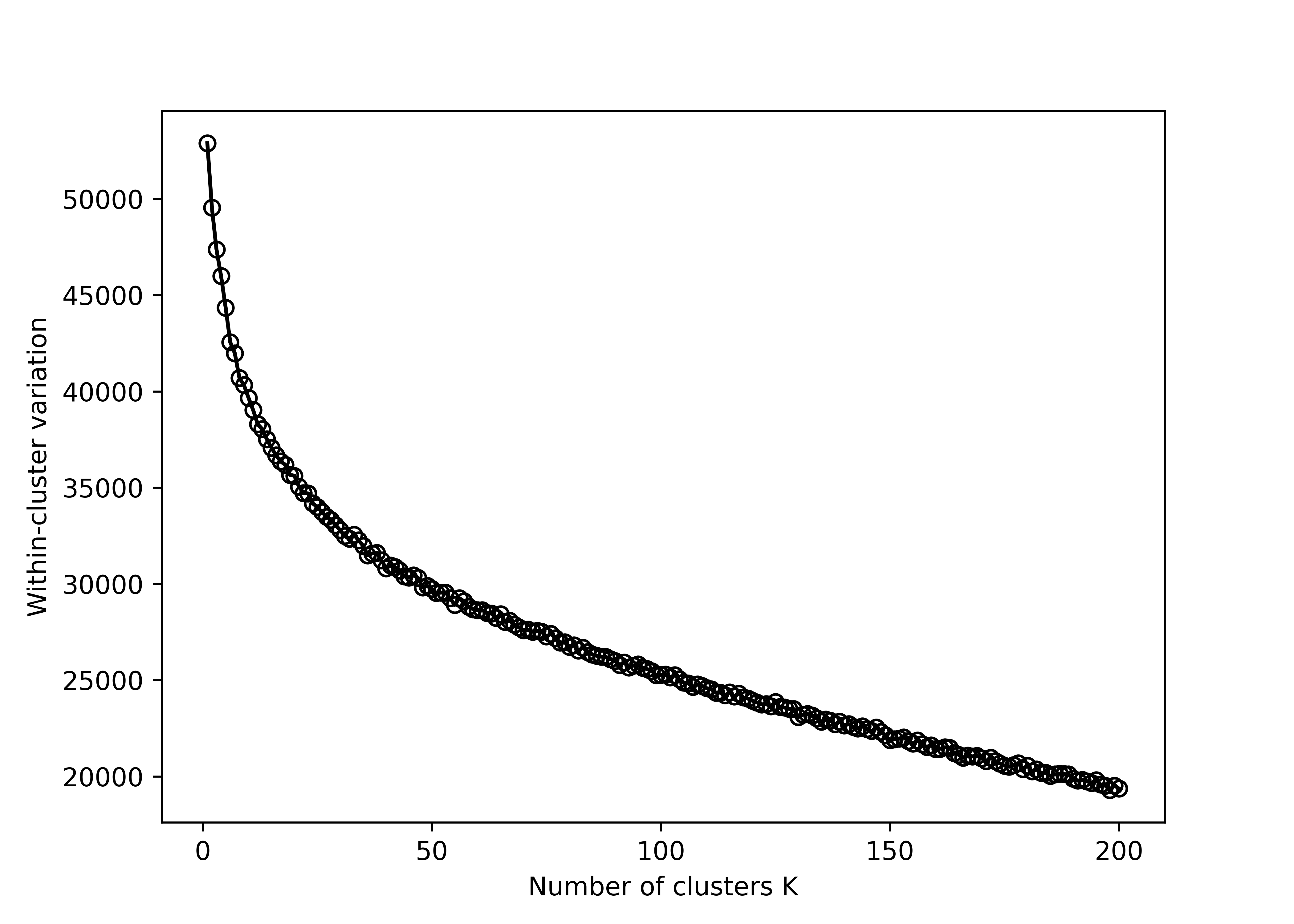
Reduce data from 2D to 1D
\boldsymbol{x}_1 \in \mathbb{R}^2 \rightarrow z_1 \in \mathbb{R} \boldsymbol{x}_2 \in \mathbb{R}^2 \rightarrow z_2 \in \mathbb{R} \vdots \boldsymbol{x}_n \in \mathbb{R}^2 \rightarrow z_n \in \mathbb{R}
The first principal component of a set of features X_1, X_2, \dots, X_p is the normalised linear combination of the features Z_1 = \phi_{11}X_1 + \phi_{21}X_2 + \dots + \phi_{p1}X_p, \qquad \sum_{j=1}^{p}\phi_{j1}^2=1 that has the largest possible variance. We find the values \phi_{11},\ldots, \phi_{p1} by maximising the sample variance of z_{i1} = \phi_{11}x_{i1} + \phi_{21}x_{i2} + \dots + \phi_{p1}x_{ip}, \quad i = 1, 2, \dots, n.
| \phi_{11}, \dots, \phi_{p1} | loadings of the first principal component |
| \phi_1 = (\phi_{11}, \dots, \phi_{p1})^T | principal component loading vector |
| z_{11}, \ldots z_{n1} | scores of the first principal component |
| \sum_{j=1}^{p}\phi_{j1}^2=1 | constraint preventing an arbitrarily large variance |
Is PCA the same as linear regression? Why or why not?
pr_comp_train <- prcomp(x_train, scale = TRUE)Error in prcomp.default(x_train, scale = TRUE): cannot rescale a constant/zero column to unit variance# Calculate the column std devs
col_std_devs <- apply(x_train, 2, sd)
col_std_devs X0 X1 X2 X3 X4 X5
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X6 X7 X8 X9 X10 X11
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X12 X13 X14 X15 X16 X17
0.0023975438 0.0052497943 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X18 X19 X20 X21 X22 X23
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X24 X25 X26 X27 X28 X29
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X30 X31 X32 X33 X34 X35
0.0000000000 0.0000000000 0.0000000000 0.0001653479 0.0036899614 0.0073450035
X36 X37 X38 X39 X40 X41
0.0145456588 0.0161569550 0.0211853119 0.0213073459 0.0208507875 0.0195538213
X42 X43 X44 X45 X46 X47
0.0229472506 0.0243856500 0.0230354157 0.0211948495 0.0151041369 0.0109502265
X48 X49 X50 X51 X52 X53
0.0111429515 0.0074043871 0.0041586589 0.0040716909 0.0000000000 0.0000000000
X54 X55 X56 X57 X58 X59
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0013227829 0.0005993860
X60 X61 X62 X63 X64 X65
0.0015278703 0.0021872664 0.0112660837 0.0184871514 0.0260346078 0.0377863192
X66 X67 X68 X69 X70 X71
0.0498183412 0.0587993685 0.0742532063 0.0868722446 0.0970276068 0.1022444891
X72 X73 X74 X75 X76 X77
0.1037216248 0.0990578542 0.0900078978 0.0784604962 0.0594138763 0.0439134399
X78 X79 X80 X81 X82 X83
0.0300459465 0.0180031871 0.0103176705 0.0048264035 0.0000000000 0.0000000000
X84 X85 X86 X87 X88 X89
0.0000000000 0.0000000000 0.0029231046 0.0021999693 0.0031267652 0.0144365906
X90 X91 X92 X93 X94 X95
0.0235975549 0.0368763029 0.0549359698 0.0806558891 0.1034517834 0.1267004759
X96 X97 X98 X99 X100 X101
0.1469704427 0.1675873509 0.1863016581 0.1961824643 0.1940990459 0.1855428973
X102 X103 X104 X105 X106 X107
0.1684581828 0.1434625432 0.1117714885 0.0840251491 0.0548280039 0.0333565830
X108 X109 X110 X111 X112 X113
0.0206945977 0.0074426467 0.0025008862 0.0000000000 0.0000000000 0.0007854023
X114 X115 X116 X117 X118 X119
0.0016478346 0.0036612400 0.0134646244 0.0321374699 0.0509432444 0.0799278946
X120 X121 X122 X123 X124 X125
0.1154464805 0.1546752411 0.1926360409 0.2317035218 0.2716569578 0.3044781100
X126 X127 X128 X129 X130 X131
0.3263933611 0.3381289688 0.3365862528 0.3197426054 0.2898037773 0.2504506846
X132 X133 X134 X135 X136 X137
0.2059416708 0.1583077694 0.1134893306 0.0769618832 0.0473984917 0.0211059585
X138 X139 X140 X141 X142 X143
0.0084390051 0.0012194404 0.0000000000 0.0000000000 0.0027490173 0.0133068103
X144 X145 X146 X147 X148 X149
0.0291276633 0.0620881177 0.1006346388 0.1441924235 0.1934205013 0.2433826935
X150 X151 X152 X153 X154 X155
0.2903942851 0.3360084396 0.3754893488 0.4035445621 0.4192750570 0.4249493791
X156 X157 X158 X159 X160 X161
0.4233785607 0.4126109454 0.3875876361 0.3495901855 0.2999739193 0.2438180847
X162 X163 X164 X165 X166 X167
0.1876762872 0.1384792634 0.0895580027 0.0433301900 0.0164846678 0.0019401623
X168 X169 X170 X171 X172 X173
0.0000000000 0.0001666326 0.0071571180 0.0244618116 0.0555749670 0.0978543977
X174 X175 X176 X177 X178 X179
0.1479310557 0.2023519892 0.2596039048 0.3148712185 0.3613562652 0.3978357098
X180 X181 X182 X183 X184 X185
0.4224877184 0.4347001797 0.4394597687 0.4404440128 0.4409606970 0.4394552790
X186 X187 X188 X189 X190 X191
0.4301763159 0.4060930008 0.3649405640 0.3073326235 0.2444537453 0.1808659669
X192 X193 X194 X195 X196 X197
0.1216325226 0.0680838340 0.0285387065 0.0060499030 0.0009714187 0.0066529077
X198 X199 X200 X201 X202 X203
0.0169891609 0.0400054333 0.0803996621 0.1312795146 0.1887286962 0.2499743170
X204 X205 X206 X207 X208 X209
0.3087726620 0.3605145561 0.3978098757 0.4217225766 0.4313450570 0.4329545487
X210 X211 X212 X213 X214 X215
0.4329147120 0.4317660948 0.4328867362 0.4342455974 0.4356967650 0.4251924267
X216 X217 X218 X219 X220 X221
0.3970977808 0.3457408707 0.2778748172 0.2068243574 0.1380788310 0.0813263153
X222 X223 X224 X225 X226 X227
0.0329937120 0.0062020185 0.0040968161 0.0115332731 0.0315337009 0.0613238584
X228 X229 X230 X231 X232 X233
0.1054949683 0.1583411928 0.2196369924 0.2847818441 0.3442461427 0.3916245948
X234 X235 X236 X237 X238 X239
0.4204547295 0.4328375185 0.4351621434 0.4362825165 0.4357872490 0.4344851675
X240 X241 X242 X243 X244 X245
0.4342518532 0.4350896826 0.4368101136 0.4321155666 0.4105216699 0.3642349234
X246 X247 X248 X249 X250 X251
0.2951143612 0.2144756703 0.1411606250 0.0837463597 0.0339756111 0.0089925978
X252 X253 X254 X255 X256 X257
0.0041720017 0.0158415532 0.0391098840 0.0747138798 0.1164589425 0.1711568555
X258 X259 X260 X261 X262 X263
0.2358423662 0.3037281700 0.3655351386 0.4088147102 0.4309680325 0.4367113356
X264 X265 X266 X267 X268 X269
0.4363649519 0.4319064084 0.4274618315 0.4262154544 0.4281986261 0.4331921096
X270 X271 X272 X273 X274 X275
0.4353465615 0.4319409154 0.4099113532 0.3642885346 0.2934395167 0.2074562342
X276 X277 X278 X279 X280 X281
0.1271976273 0.0690142930 0.0286450614 0.0085272950 0.0058466163 0.0179800177
X282 X283 X284 X285 X286 X287
0.0405585003 0.0734343438 0.1168545046 0.1723342098 0.2418783946 0.3127238019
X288 X289 X290 X291 X292 X293
0.3770363402 0.4166093232 0.4327740111 0.4341654968 0.4233518520 0.4081036588
X294 X295 X296 X297 X298 X299
0.4032828213 0.4115321908 0.4204075713 0.4303675275 0.4331048373 0.4278002294
X300 X301 X302 X303 X304 X305
0.4017905814 0.3527881867 0.2810933095 0.1943243365 0.1105542500 0.0553750184
X306 X307 X308 X309 X310 X311
0.0245722049 0.0066431069 0.0033361055 0.0157001643 0.0351395547 0.0616190411
X312 X313 X314 X315 X316 X317
0.1067187712 0.1672683599 0.2438265607 0.3222590618 0.3877509652 0.4225219322
X318 X319 X320 X321 X322 X323
0.4316815281 0.4264816816 0.4073311151 0.3915075871 0.4023588809 0.4168865045
X324 X325 X326 X327 X328 X329
0.4230625087 0.4312911943 0.4330271334 0.4236289963 0.3885603541 0.3338243393
X330 X331 X332 X333 X334 X335
0.2704180761 0.1911699629 0.1037155061 0.0408090494 0.0194328456 0.0017400693
X336 X337 X338 X339 X340 X341
0.0036269159 0.0093750333 0.0264666545 0.0514306440 0.0966865374 0.1667231726
X342 X343 X344 X345 X346 X347
0.2524819313 0.3365365105 0.3979850830 0.4271159557 0.4317571623 0.4243491536
X348 X349 X350 X351 X352 X353
0.4078521737 0.4031716033 0.4267092473 0.4342487174 0.4304302162 0.4350684398
X354 X355 X356 X357 X358 X359
0.4361847444 0.4179091072 0.3728544714 0.3194488875 0.2627657572 0.1949262110
X360 X361 X362 X363 X364 X365
0.1095524031 0.0345719068 0.0153911796 0.0034160062 0.0006613914 0.0078608042
X366 X367 X368 X369 X370 X371
0.0204635838 0.0438785363 0.0946998643 0.1734312060 0.2672779695 0.3507841386
X372 X373 X374 X375 X376 X377
0.4061152412 0.4293236579 0.4318550514 0.4241465517 0.4158638501 0.4261251847
X378 X379 X380 X381 X382 X383
0.4462134012 0.4378142097 0.4311984075 0.4394967438 0.4375774957 0.4115354833
X384 X385 X386 X387 X388 X389
0.3637641406 0.3167368049 0.2653261354 0.2032616122 0.1222290366 0.0409479179
X390 X391 X392 X393 X394 X395
0.0152019234 0.0054097807 0.0023355384 0.0052285119 0.0130799227 0.0374799291
X396 X397 X398 X399 X400 X401
0.0956686151 0.1873269285 0.2829103439 0.3610484407 0.4102569593 0.4289677146
X402 X403 X404 X405 X406 X407
0.4301532847 0.4247911309 0.4233711651 0.4368619948 0.4456554430 0.4291513162
X408 X409 X410 X411 X412 X413
0.4305949908 0.4405736497 0.4363075147 0.4089349511 0.3676239422 0.3236634532
X414 X415 X416 X417 X418 X419
0.2727973143 0.2097172558 0.1286291381 0.0471448847 0.0147375407 0.0010765465
X420 X421 X422 X423 X424 X425
0.0007782955 0.0046727192 0.0102152260 0.0379512740 0.1010350343 0.2030017470
X426 X427 X428 X429 X430 X431
0.2951933967 0.3639068725 0.4062228957 0.4245518048 0.4256587376 0.4246870345
X432 X433 X434 X435 X436 X437
0.4291160944 0.4414005502 0.4420727017 0.4292733791 0.4366878213 0.4415963698
X438 X439 X440 X441 X442 X443
0.4309286353 0.4080562291 0.3727597853 0.3320994053 0.2779615218 0.2097512450
X444 X445 X446 X447 X448 X449
0.1272463559 0.0539684815 0.0178885496 0.0033482941 0.0008267393 0.0029940784
X450 X451 X452 X453 X454 X455
0.0138228271 0.0412221631 0.1104637534 0.2170135511 0.3023797339 0.3595832262
X456 X457 X458 X459 X460 X461
0.3947447705 0.4122993593 0.4158493263 0.4206965885 0.4314989625 0.4427050272
X462 X463 X464 X465 X466 X467
0.4417362276 0.4361954559 0.4402239838 0.4359127905 0.4250439053 0.4070645579
X468 X469 X470 X471 X472 X473
0.3786829820 0.3338784508 0.2755223456 0.2026331396 0.1229471911 0.0579912547
X474 X475 X476 X477 X478 X479
0.0200523894 0.0004133696 0.0000000000 0.0041281538 0.0179872028 0.0505789352
X480 X481 X482 X483 X484 X485
0.1298555939 0.2297901036 0.3054559836 0.3532966185 0.3818870883 0.3972079631
X486 X487 X488 X489 X490 X491
0.4047129993 0.4132523582 0.4254020668 0.4346824827 0.4392184656 0.4382369908
X492 X493 X494 X495 X496 X497
0.4350850345 0.4300895149 0.4238421699 0.4093677407 0.3801320452 0.3297761773
X498 X499 X500 X501 X502 X503
0.2644720521 0.1905565582 0.1168439057 0.0585376412 0.0206661228 0.0011590804
X504 X505 X506 X507 X508 X509
0.0012416563 0.0042313652 0.0221883087 0.0649319505 0.1489302820 0.2419647509
X510 X511 X512 X513 X514 X515
0.3121254470 0.3541330615 0.3776212774 0.3918440677 0.4020502183 0.4096388287
X516 X517 X518 X519 X520 X521
0.4171205246 0.4281514022 0.4362249492 0.4352919931 0.4318112613 0.4314409311
X522 X523 X524 X525 X526 X527
0.4273254218 0.4110290047 0.3739615302 0.3181696180 0.2516929918 0.1800180323
X528 X529 X530 X531 X532 X533
0.1112411669 0.0581123002 0.0169972924 0.0047397932 0.0003100272 0.0051773681
X534 X535 X536 X537 X538 X539
0.0301479215 0.0769465565 0.1615108012 0.2506643964 0.3199322639 0.3623965831
X540 X541 X542 X543 X544 X545
0.3872562073 0.4024395307 0.4127264392 0.4196326032 0.4253076134 0.4325108270
X546 X547 X548 X549 X550 X551
0.4367517599 0.4349395624 0.4333295906 0.4351565204 0.4271945888 0.4023701720
X552 X553 X554 X555 X556 X557
0.3586358827 0.2992614174 0.2316994532 0.1621220753 0.1014334680 0.0541328336
X558 X559 X560 X561 X562 X563
0.0184248328 0.0037731996 0.0000000000 0.0066814240 0.0296872868 0.0809702884
X564 X565 X566 X567 X568 X569
0.1601866059 0.2456248000 0.3191662464 0.3706205155 0.4008114723 0.4180238575
X570 X571 X572 X573 X574 X575
0.4274912471 0.4321569966 0.4354597571 0.4376282869 0.4366339483 0.4361008624
X576 X577 X578 X579 X580 X581
0.4365117877 0.4327724352 0.4177101586 0.3829224294 0.3283560136 0.2643082056
X582 X583 X584 X585 X586 X587
0.1978442060 0.1371406251 0.0889249988 0.0455137403 0.0170766780 0.0010334241
X588 X589 X590 X591 X592 X593
0.0000000000 0.0056887471 0.0278403486 0.0713215698 0.1381258499 0.2212972415
X594 X595 X596 X597 X598 X599
0.3013896862 0.3651928235 0.4048448513 0.4263843684 0.4363376889 0.4369197583
X600 X601 X602 X603 X604 X605
0.4360963773 0.4333005181 0.4337352862 0.4351906629 0.4337374584 0.4209236777
X606 X607 X608 X609 X610 X611
0.3904500771 0.3405633317 0.2791248592 0.2143460989 0.1572603537 0.1098940122
X612 X613 X614 X615 X616 X617
0.0700950723 0.0336420839 0.0118081285 0.0000000000 0.0000000000 0.0001666326
X618 X619 X620 X621 X622 X623
0.0210710335 0.0520055381 0.1036316627 0.1755203816 0.2547135682 0.3282561545
X624 X625 X626 X627 X628 X629
0.3847969407 0.4199819466 0.4366818970 0.4422227789 0.4406946709 0.4396525612
X630 X631 X632 X633 X634 X635
0.4398671320 0.4364909265 0.4202644159 0.3875919645 0.3388666995 0.2781557128
X636 X637 X638 X639 X640 X641
0.2176858826 0.1623733490 0.1173758205 0.0820725002 0.0483444637 0.0184264589
X642 X643 X644 X645 X646 X647
0.0057211268 0.0000000000 0.0000000000 0.0000000000 0.0112217186 0.0297570686
X648 X649 X650 X651 X652 X653
0.0660743322 0.1161213649 0.1806824012 0.2532460299 0.3211018066 0.3748145765
X654 X655 X656 X657 X658 X659
0.4097159069 0.4280422997 0.4336064421 0.4323575031 0.4230039642 0.4030340952
X660 X661 X662 X663 X664 X665
0.3675682690 0.3190647081 0.2622722014 0.2061035144 0.1573877143 0.1148461140
X666 X667 X668 X669 X670 X671
0.0805076591 0.0520468110 0.0310056458 0.0116517327 0.0039629731 0.0000000000
X672 X673 X674 X675 X676 X677
0.0000000000 0.0000000000 0.0076144977 0.0173888799 0.0370082023 0.0653554911
X678 X679 X680 X681 X682 X683
0.1075706479 0.1595612574 0.2148639938 0.2727706801 0.3182468147 0.3463647529
X684 X685 X686 X687 X688 X689
0.3574259379 0.3560643082 0.3389324293 0.3077657829 0.2709015171 0.2300796285
X690 X691 X692 X693 X694 X695
0.1860283342 0.1457015662 0.1084865799 0.0771752397 0.0515780249 0.0316404240
X696 X697 X698 X699 X700 X701
0.0160654499 0.0081731020 0.0020593839 0.0000000000 0.0000000000 0.0000000000
X702 X703 X704 X705 X706 X707
0.0009289242 0.0077364835 0.0178183397 0.0351419473 0.0634944771 0.0974766847
X708 X709 X710 X711 X712 X713
0.1372418044 0.1727874420 0.2041750702 0.2224688351 0.2313550389 0.2298700409
X714 X715 X716 X717 X718 X719
0.2149963608 0.1934191049 0.1729444505 0.1504885979 0.1238798906 0.0967324056
X720 X721 X722 X723 X724 X725
0.0709899590 0.0492367765 0.0322442759 0.0188537849 0.0077086161 0.0031816969
X726 X727 X728 X729 X730 X731
0.0021495221 0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0000000000
X732 X733 X734 X735 X736 X737
0.0087394641 0.0196112451 0.0398514730 0.0616593210 0.0831733932 0.1023871467
X738 X739 X740 X741 X742 X743
0.1203700365 0.1345978781 0.1392057277 0.1406063581 0.1305035652 0.1132680958
X744 X745 X746 X747 X748 X749
0.0979993420 0.0847458710 0.0705027825 0.0553044058 0.0405982457 0.0264110547
X750 X751 X752 X753 X754 X755
0.0149790253 0.0045307643 0.0000000000 0.0012194404 0.0000000000 0.0000000000
X756 X757 X758 X759 X760 X761
0.0000000000 0.0000000000 0.0000000000 0.0000000000 0.0022150671 0.0085515203
X762 X763 X764 X765 X766 X767
0.0119449865 0.0181448047 0.0181015629 0.0221735013 0.0277901909 0.0362742510
X768 X769 X770 X771 X772 X773
0.0391687788 0.0425295650 0.0468867824 0.0434324116 0.0386096876 0.0334878510
X774 X775 X776 X777 X778 X779
0.0264272255 0.0159713074 0.0132575854 0.0074380065 0.0062421598 0.0011987719
X780 X781 X782 X783
0.0000000000 0.0000000000 0.0000000000 0.0000000000 # Calculate the column std devs
col_std_devs = np.std(x_train, axis=0)
col_std_devsarray([0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0.00632139, 0. , 0. , 0. , 0. ,
0. , 0.00471006, 0.03209272, 0.03160696, 0.01884881,
0.04456476, 0.02154137, 0.00756088, 0.02702085, 0.00669324,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.01710494, 0.03160696, 0.02661873,
0.05510879, 0.05450345, 0.05931561, 0.04863671, 0.08549198,
0.10741047, 0.11400141, 0.11074189, 0.10932877, 0.08365742,
0.05245761, 0.06270962, 0.04839488, 0.02379265, 0.00632139,
0.0271448 , 0.02045156, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.00577117,
0.04018833, 0.0475317 , 0.06717571, 0.09542121, 0.1172866 ,
0.1326602 , 0.14192618, 0.15727922, 0.17698733, 0.19413856,
0.20136337, 0.19530441, 0.16554901, 0.14571768, 0.11746599,
0.08029755, 0.04447169, 0.0244046 , 0.02553347, 0.02379818,
0. , 0. , 0. , 0. , 0. ,
0.00656929, 0.00655459, 0.04559703, 0.06879667, 0.08678023,
0.12528062, 0.1684035 , 0.20054473, 0.2368673 , 0.27466526,
0.30847638, 0.32736406, 0.33448038, 0.33900105, 0.31503969,
0.29049059, 0.26078476, 0.22017518, 0.15598105, 0.12052318,
0.08170073, 0.05018388, 0.02931361, 0. , 0. ,
0. , 0. , 0. , 0.01455365, 0.03951559,
0.08060715, 0.11767611, 0.15020234, 0.18591748, 0.23488908,
0.28291749, 0.33369558, 0.37076557, 0.40602963, 0.42472318,
0.42954076, 0.42614594, 0.41963032, 0.40081935, 0.36864185,
0.3133172 , 0.25574168, 0.19666616, 0.14096531, 0.0975862 ,
0.06137734, 0. , 0. , 0. , 0. ,
0. , 0.04251863, 0.07955513, 0.11784335, 0.15438208,
0.19966702, 0.25692918, 0.30765373, 0.35854544, 0.39953659,
0.4268652 , 0.44002132, 0.43798439, 0.43810079, 0.44462634,
0.44359873, 0.43428741, 0.41312875, 0.37855436, 0.32225983,
0.24497018, 0.18651777, 0.1286197 , 0.06941716, 0.00148739,
0. , 0. , 0. , 0.01405165, 0.04329843,
0.08316314, 0.12220062, 0.1958706 , 0.25097463, 0.30807203,
0.35901591, 0.40279701, 0.4245412 , 0.43052727, 0.42907545,
0.43296095, 0.43524142, 0.43237627, 0.43877196, 0.437274 ,
0.42270895, 0.40531489, 0.35847083, 0.28094202, 0.1969408 ,
0.13916466, 0.08819644, 0.0139584 , 0. , 0. ,
0. , 0.03582303, 0.07273479, 0.09887056, 0.1483185 ,
0.21183447, 0.27821159, 0.33976125, 0.38635678, 0.4248203 ,
0.43537696, 0.43548349, 0.43220226, 0.4350645 , 0.43583428,
0.4341156 , 0.43393472, 0.43685591, 0.4251527 , 0.42005168,
0.37958657, 0.30095363, 0.19131187, 0.12169742, 0.07804139,
0.0170286 , 0. , 0. , 0. , 0.03065764,
0.06923245, 0.11089565, 0.16065397, 0.22535589, 0.29438402,
0.36097261, 0.40956782, 0.43080713, 0.43870243, 0.43031281,
0.43195262, 0.42486633, 0.42298901, 0.42659393, 0.43542706,
0.4379478 , 0.43288453, 0.41466813, 0.37449193, 0.30477767,
0.20430191, 0.11850108, 0.06290817, 0.00272688, 0. ,
0. , 0. , 0.02048843, 0.07276159, 0.10913294,
0.16245558, 0.23893697, 0.31134657, 0.37838729, 0.41475112,
0.43253241, 0.42911084, 0.42813896, 0.40398312, 0.39273926,
0.40173905, 0.41578855, 0.42738294, 0.43213101, 0.42819755,
0.39729331, 0.35478423, 0.29766405, 0.20898936, 0.10127237,
0.04854295, 0.00099159, 0. , 0. , 0. ,
0.02178642, 0.06057097, 0.09217747, 0.16592649, 0.24492413,
0.32839423, 0.38879821, 0.42059238, 0.43659809, 0.43150282,
0.40965518, 0.3858331 , 0.39566996, 0.41195661, 0.4273496 ,
0.43368373, 0.43361747, 0.4279557 , 0.37853231, 0.3284051 ,
0.28086668, 0.20850073, 0.08788801, 0.04184626, 0. ,
0. , 0. , 0. , 0.00237982, 0.03801724,
0.07875916, 0.16905464, 0.25133786, 0.33609416, 0.38994536,
0.42894532, 0.43894564, 0.42056849, 0.40279993, 0.39757374,
0.41576869, 0.43401752, 0.43495665, 0.43841228, 0.43265986,
0.41151659, 0.35869768, 0.3128902 , 0.26971618, 0.2140111 ,
0.10436712, 0.03468962, 0. , 0. , 0. ,
0. , 0. , 0.03845491, 0.09539211, 0.17804007,
0.26373664, 0.34529475, 0.39837988, 0.43601761, 0.44263179,
0.42029338, 0.41610261, 0.42114307, 0.4393086 , 0.4387737 ,
0.43035438, 0.43207914, 0.43840201, 0.40147432, 0.35235213,
0.30723513, 0.27118421, 0.21412765, 0.12096702, 0.02827168,
0. , 0. , 0. , 0. , 0. ,
0.02040602, 0.11062953, 0.18608279, 0.27081147, 0.35291778,
0.40640852, 0.42859704, 0.42801721, 0.42691026, 0.42339514,
0.43711525, 0.44568005, 0.43464572, 0.42646292, 0.43931709,
0.4321966 , 0.40257852, 0.36666728, 0.32669606, 0.27650885,
0.21719402, 0.12579285, 0.02693422, 0. , 0. ,
0. , 0. , 0. , 0.05628161, 0.1209559 ,
0.20712795, 0.29269382, 0.36254235, 0.40468346, 0.41959646,
0.42444973, 0.43129793, 0.43439108, 0.43926889, 0.44002337,
0.42434805, 0.43150579, 0.44395702, 0.42525305, 0.39565276,
0.3710153 , 0.33734366, 0.28084273, 0.20224602, 0.13196476,
0.06072177, 0.02723402, 0.01053565, 0. , 0. ,
0.00780878, 0.07050808, 0.13477738, 0.23050149, 0.30641081,
0.35779202, 0.38875958, 0.41895785, 0.42233559, 0.42572083,
0.43206811, 0.44035815, 0.44171571, 0.43530775, 0.43887727,
0.43956203, 0.41660005, 0.39467921, 0.37035814, 0.33471491,
0.2747054 , 0.20549548, 0.13002109, 0.06968553, 0.0442286 ,
0.02169105, 0. , 0. , 0.00464369, 0.07756347,
0.15877126, 0.25279079, 0.31454055, 0.35784455, 0.3809416 ,
0.40144353, 0.40663051, 0.41241853, 0.42470234, 0.43362445,
0.44163663, 0.44254793, 0.43944648, 0.43211477, 0.41738909,
0.39492234, 0.36953941, 0.3317193 , 0.2626028 , 0.19201395,
0.13238253, 0.06487699, 0.00720873, 0.00111554, 0. ,
0. , 0.01684228, 0.08041132, 0.17250332, 0.26218738,
0.3248206 , 0.3565772 , 0.37837721, 0.39325732, 0.40753051,
0.41356328, 0.41508733, 0.42915652, 0.4377368 , 0.44214895,
0.43181103, 0.43291154, 0.41808596, 0.40335883, 0.3707025 ,
0.33061227, 0.25877329, 0.19474455, 0.11757695, 0.05599719,
0.01834443, 0. , 0. , 0. , 0.02471679,
0.07774463, 0.17312389, 0.26261951, 0.33280211, 0.36512418,
0.39278746, 0.40524247, 0.41941539, 0.42244945, 0.42990087,
0.43183523, 0.442817 , 0.43678112, 0.42812915, 0.4307606 ,
0.41439324, 0.3964843 , 0.36211405, 0.31375972, 0.24265572,
0.1533867 , 0.08873031, 0.03609946, 0. , 0. ,
0. , 0. , 0.01673491, 0.0878077 , 0.16304726,
0.25137123, 0.3246157 , 0.3734039 , 0.41249505, 0.42235997,
0.43254136, 0.43259603, 0.43415667, 0.43123241, 0.43842367,
0.43184913, 0.43846301, 0.43380995, 0.40900249, 0.38154089,
0.33292645, 0.27917957, 0.19386896, 0.11012857, 0.07221584,
0.02042215, 0. , 0. , 0. , 0. ,
0.01378692, 0.08132795, 0.15189211, 0.21438286, 0.28840979,
0.36840071, 0.41004159, 0.42827406, 0.43113866, 0.43688584,
0.43033746, 0.42712919, 0.43576115, 0.42755436, 0.43733179,
0.42814368, 0.39151762, 0.34495823, 0.293887 , 0.23274446,
0.16904924, 0.10652938, 0.07903019, 0.01650713, 0. ,
0. , 0. , 0. , 0.03238282, 0.06049343,
0.11717767, 0.16491966, 0.24545798, 0.32541922, 0.38356558,
0.42085985, 0.43587465, 0.44668427, 0.44120495, 0.44284122,
0.43889708, 0.43502263, 0.42820984, 0.40150819, 0.34295293,
0.29524292, 0.24341204, 0.18979504, 0.13346593, 0.07845627,
0.05541322, 0.02222853, 0. , 0. , 0. ,
0. , 0.00522838, 0.03210987, 0.06110345, 0.09082982,
0.16572395, 0.24606533, 0.30672635, 0.37861919, 0.41689056,
0.42913179, 0.43672322, 0.43200321, 0.42842794, 0.41181975,
0.38165377, 0.32733816, 0.26392393, 0.22245658, 0.1788245 ,
0.12239288, 0.0802762 , 0.02949714, 0.03141965, 0.00966801,
0. , 0. , 0. , 0. , 0. ,
0. , 0.03472836, 0.05462183, 0.09760728, 0.14279819,
0.20792451, 0.27632276, 0.32245713, 0.35391792, 0.36714246,
0.35752738, 0.33836146, 0.3040463 , 0.27087976, 0.22000658,
0.16771057, 0.15002924, 0.11684203, 0.07906187, 0.0494708 ,
0.00123949, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.02622224,
0.04349002, 0.05739445, 0.09030618, 0.13443827, 0.1898996 ,
0.20480971, 0.23124963, 0.23451802, 0.21877729, 0.20908306,
0.19869266, 0.18366167, 0.15691439, 0.12366887, 0.08516472,
0.06247883, 0.0306758 , 0.01016381, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.00471006, 0.04329773, 0.02634197, 0.03002963,
0.03968821, 0.08594586, 0.10335321, 0.11229515, 0.12650289,
0.13894268, 0.12570129, 0.12727757, 0.12327982, 0.09066604,
0.07668645, 0.07073178, 0.05674737, 0.03547014, 0.01319718,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0.00309872, 0.02540952,
0.03123511, 0.00780964, 0.01165119, 0.02138761, 0.03160658,
0.02340193, 0.04013821, 0.02528557, 0.00260293, 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. ])pr_comp_train <- prcomp(x_train)
pve <- pr_comp_train$sdev^2 / sum(pr_comp_train$sdev^2)# Do it again using ggplot
data.frame(pve) %>%
ggplot(aes(x = 1:length(pve), y = pve)) +
geom_point() +
geom_line() +
labs(x = 'Principal Component', y = 'Proportion of Variance Explained')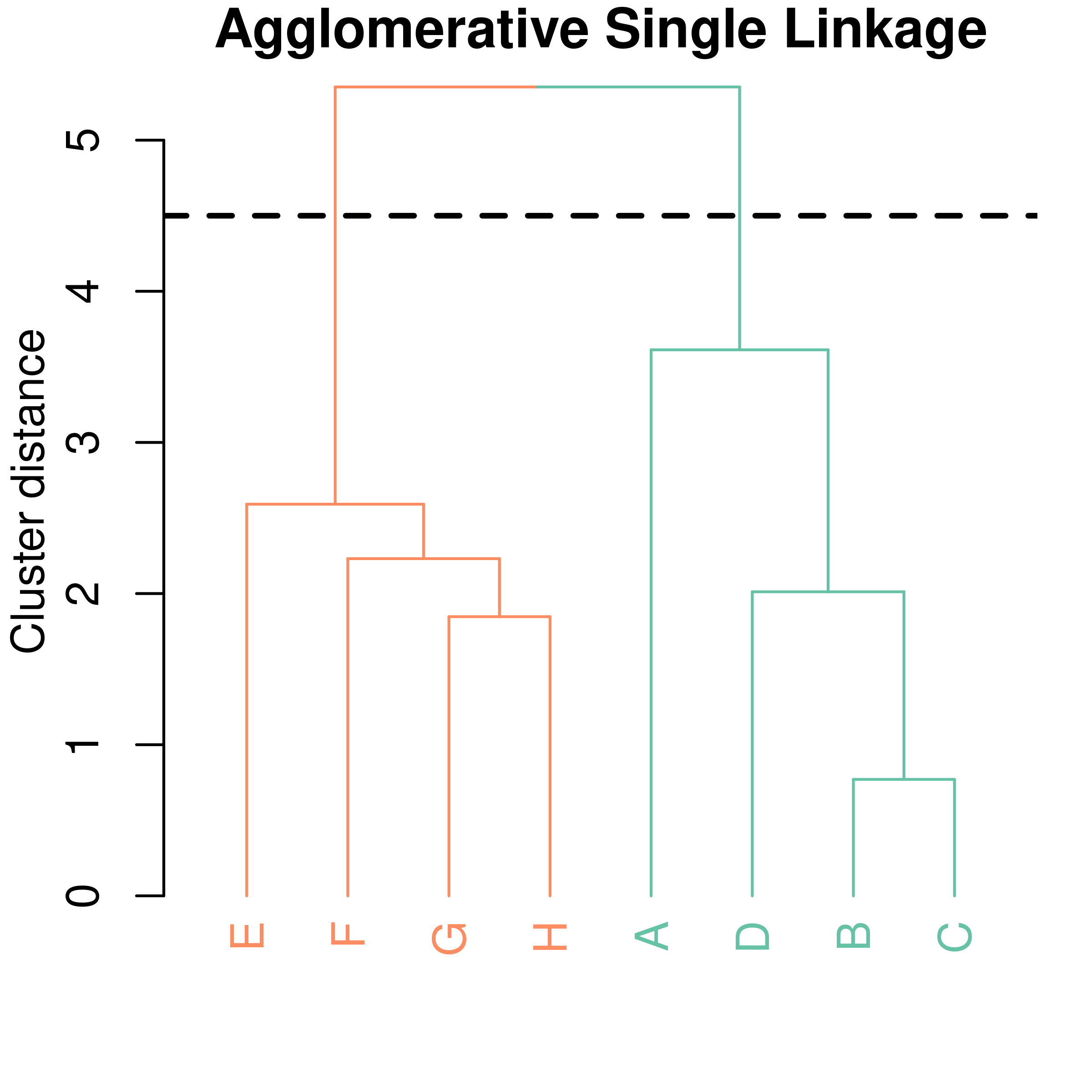
pca = PCA()
pr_out = pca.fit(x_train)
pve = (pr_out.explained_variance_ ** 2) / np.sum(pr_out.explained_variance_ ** 2)plt.figure(figsize=(8, 4))
plt.plot(pve, marker='o', linestyle = '', mfc = 'none', color='black')
plt.xlabel('Principal Component')
plt.ylabel('Proportion of Variance Explained')
plt.xticks(np.arange(0, 1000, step=200));

A scree plot is a line plot of the eigenvalues of principal components on the y-axis and the factors on the x-axis.
The scree plot is used to determine the number of factors to retain in a principal components analysis.
The point at which the line starts to level off is the number of factors to retain.
cve <- cumsum(pve)data.frame(cve) %>%
ggplot(aes(x = 1:length(cve), y = cve)) +
geom_point() +
geom_line() +
labs(x = 'Principal Component', y = 'Cumulative Prop. Variance Explained')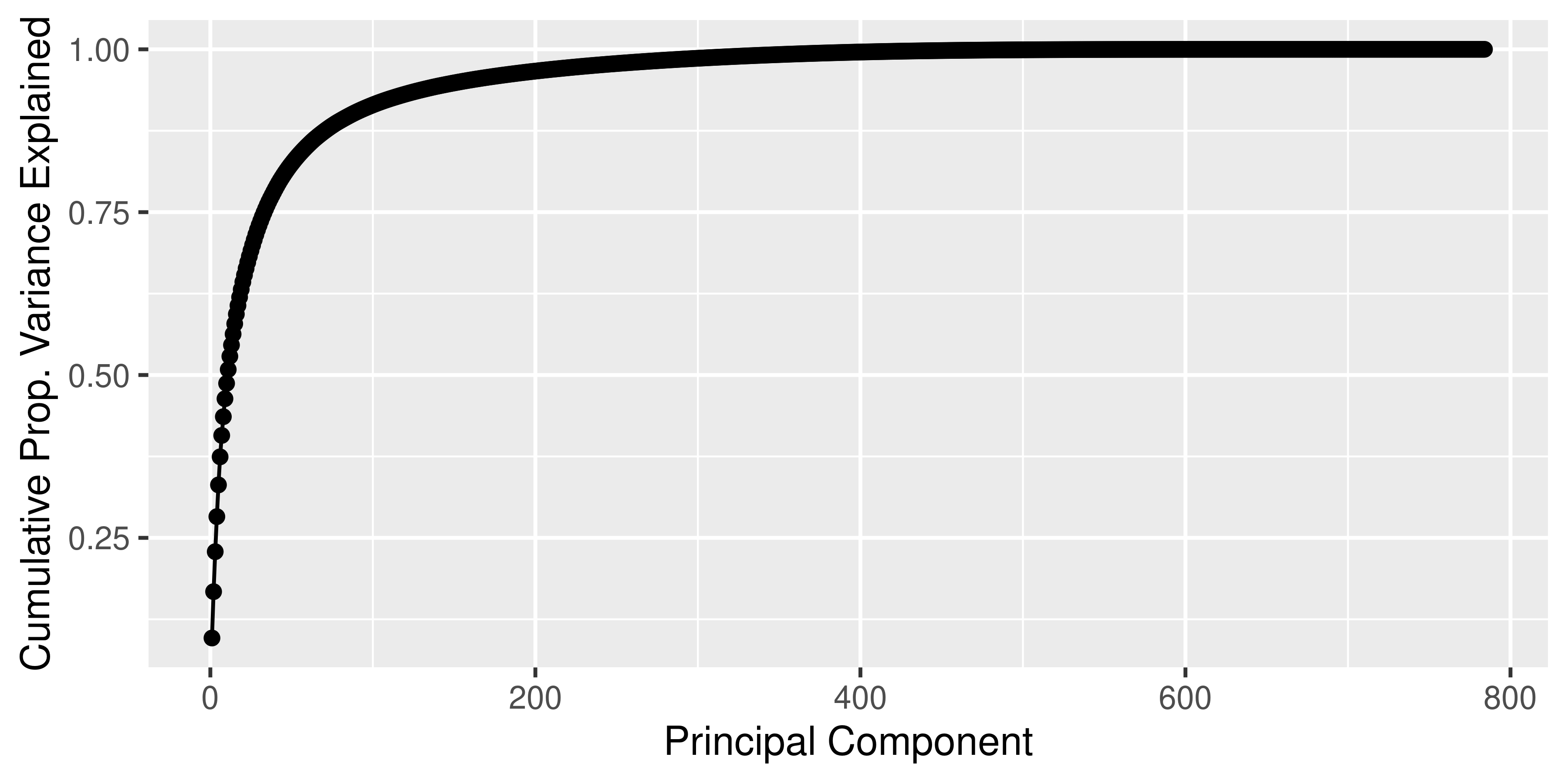
cve = np.cumsum(pve)plt.figure(figsize=(8, 4))
plt.plot(cve, marker='o', linestyle = '', mfc = 'none', color='black')
plt.xlabel('Principal Component')
plt.ylabel('Cumulative Proportion of Variance Explained')
plt.xticks(np.arange(0, 1000, step=200));
plt.yticks(np.arange(0, 1, step=0.2));
plt.show()
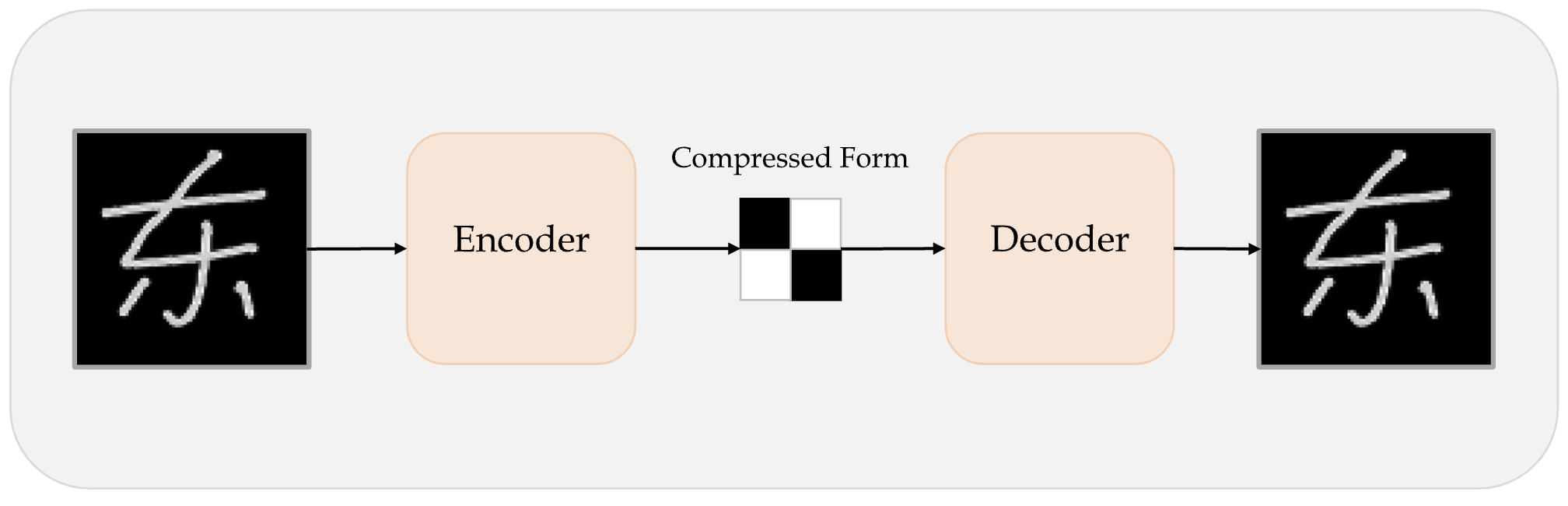
An autoencoder takes an observation, maps it to a latent space via an encoder module, then decodes it back to an output with the same dimensions via a decoder module.
# Perform PCA on non-zero variance columns
non_zero_var_cols <- which(col_std_devs != 0)
pca <- prcomp(x_train[, non_zero_var_cols], center = TRUE, scale. = TRUE)
pca_train_full <- predict(pca, newdata = x_train[, non_zero_var_cols])
indices <- c()
for (digit in 0:9) {
for (i in seq_along(y_train)) {
if (y_train[i] == digit) {
indices <- c(indices, i)
break
}
}
}
pca_autoencoder <- function(pca_train_full, num_components) {
pca_train <- pca_train_full[, 1:num_components]
# Inverse transform from the PCA reduced space back to the original space
pca_reconstructed <- pca_train %*% t(pca$rotation[, 1:num_components])
pca_reconstructed <- scale(pca_reconstructed, center = -pca$center, scale = FALSE)
# Create a full reconstructed dataset with zero-variance columns
pca_reconstructed_full <- matrix(0, nrow = nrow(x_train), ncol = 784)
pca_reconstructed_full[, non_zero_var_cols] <- pca_reconstructed
pca_reconstructed_full <- pmin(pmax(pca_reconstructed_full, 0), 1)
pca_reconstructed_full
}
plot_reconstructions <- function(x_train, pca_reconstructed_full, indices) {
par(mfrow = c(2, 5))
for (index in indices[1:5]) {
plot_digit(x_train[index, ])
}
for (index in indices[1:5]) {
plot_digit(pca_reconstructed_full[index,])
}
}num_components <- 400
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[1:5])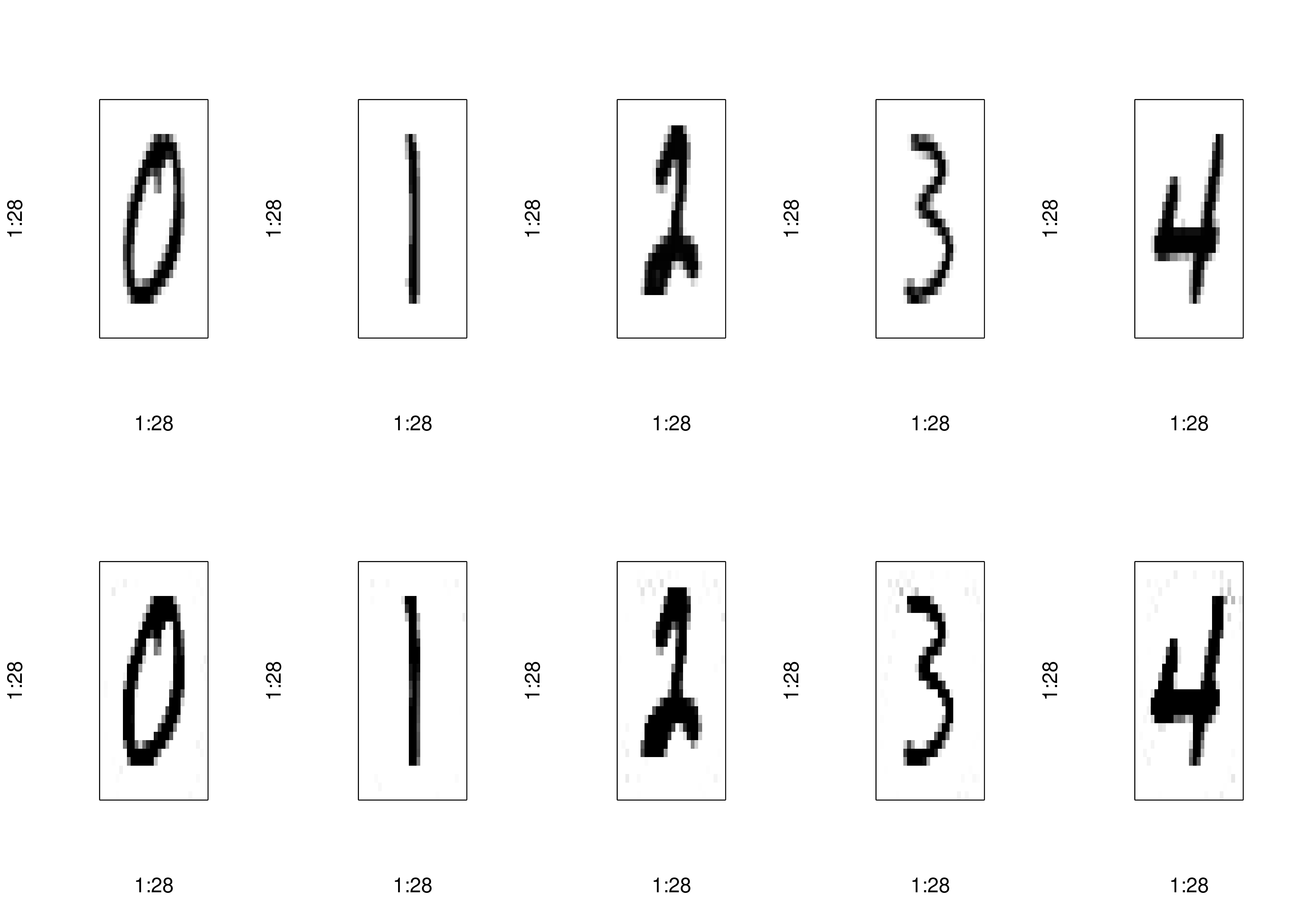
num_components <- 100
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[1:5])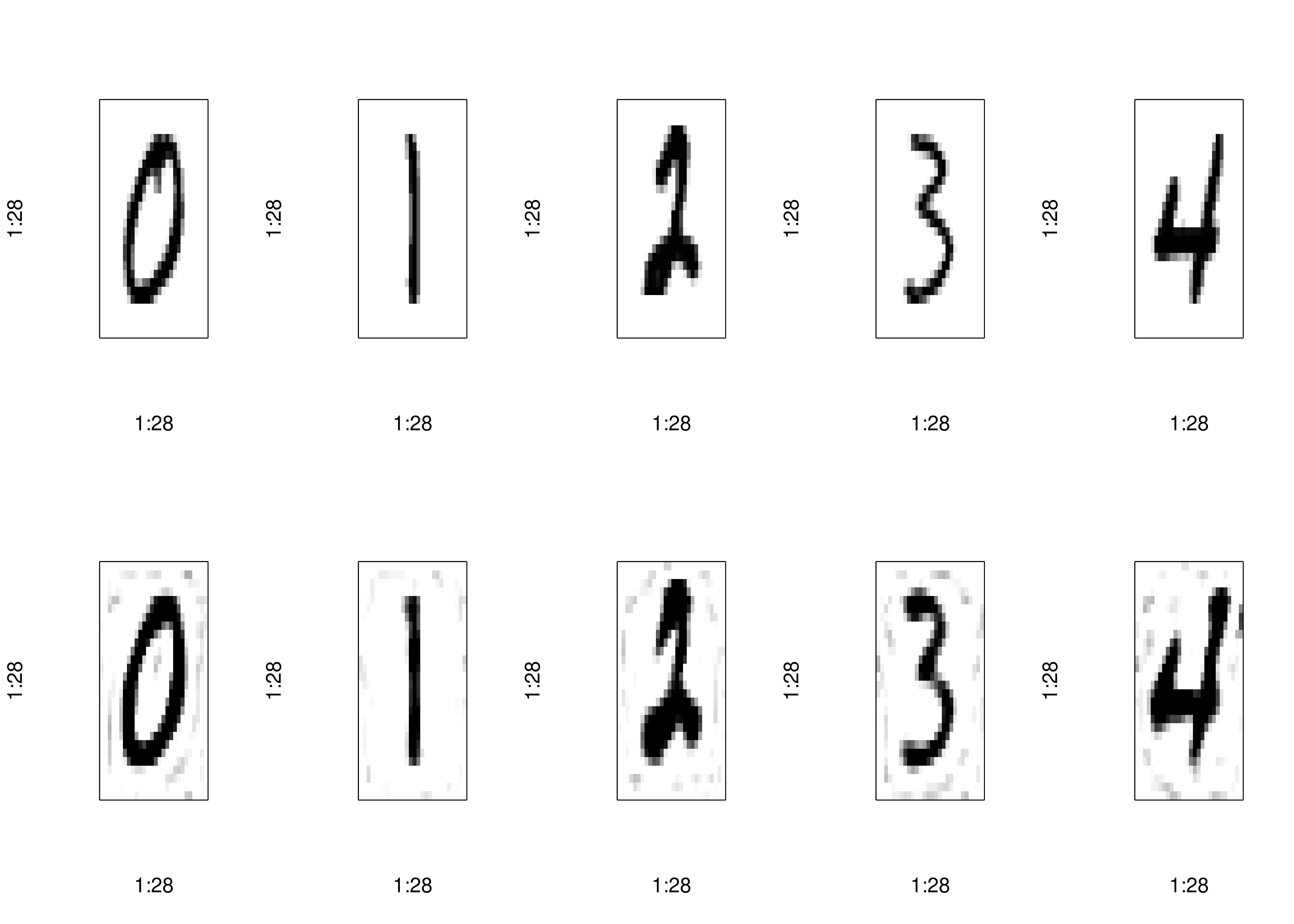
num_components <- 25
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[1:5])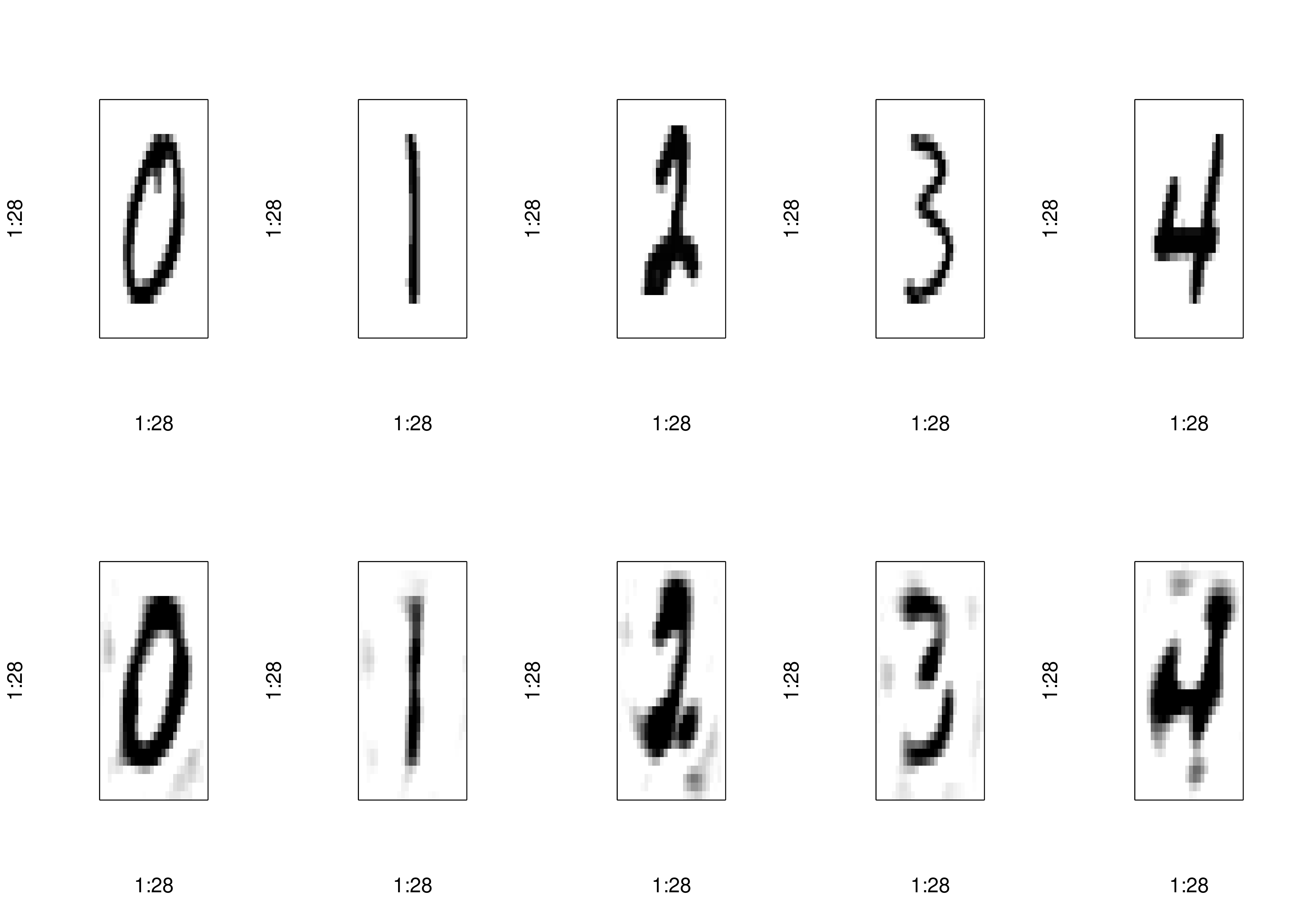
num_components <- 10
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[1:5])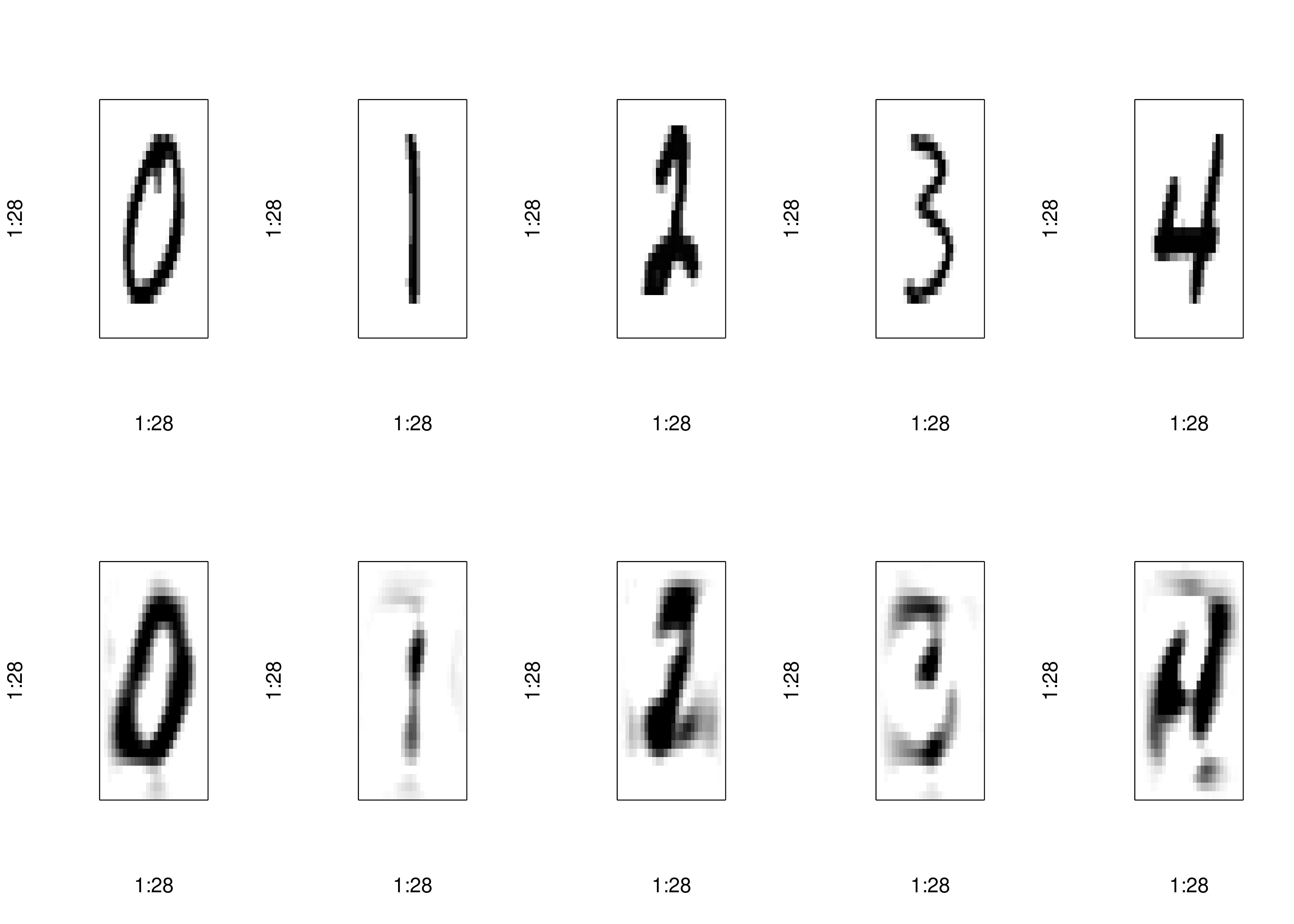
num_components <- 5
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[1:5])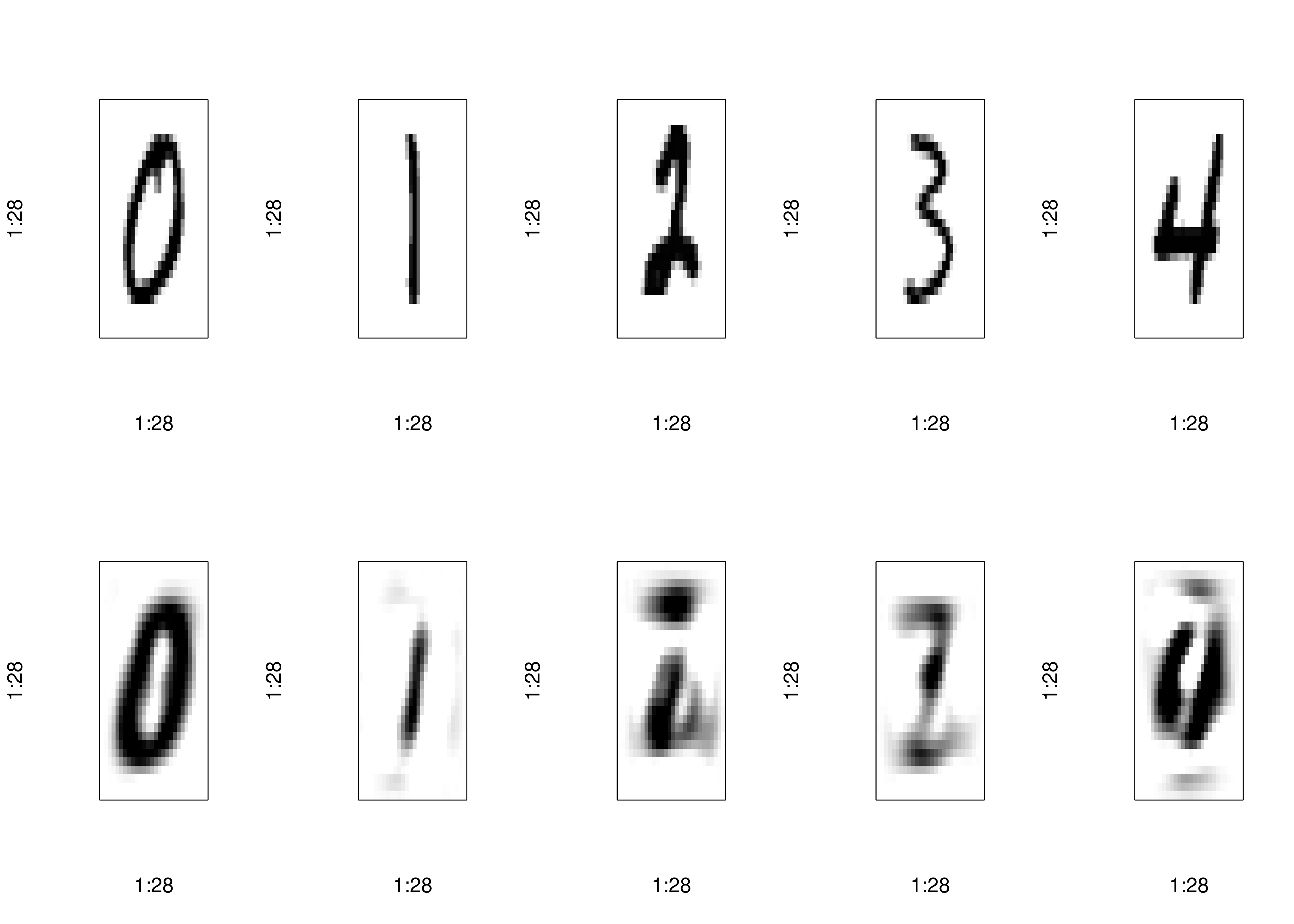
num_components <- 400
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[6:10])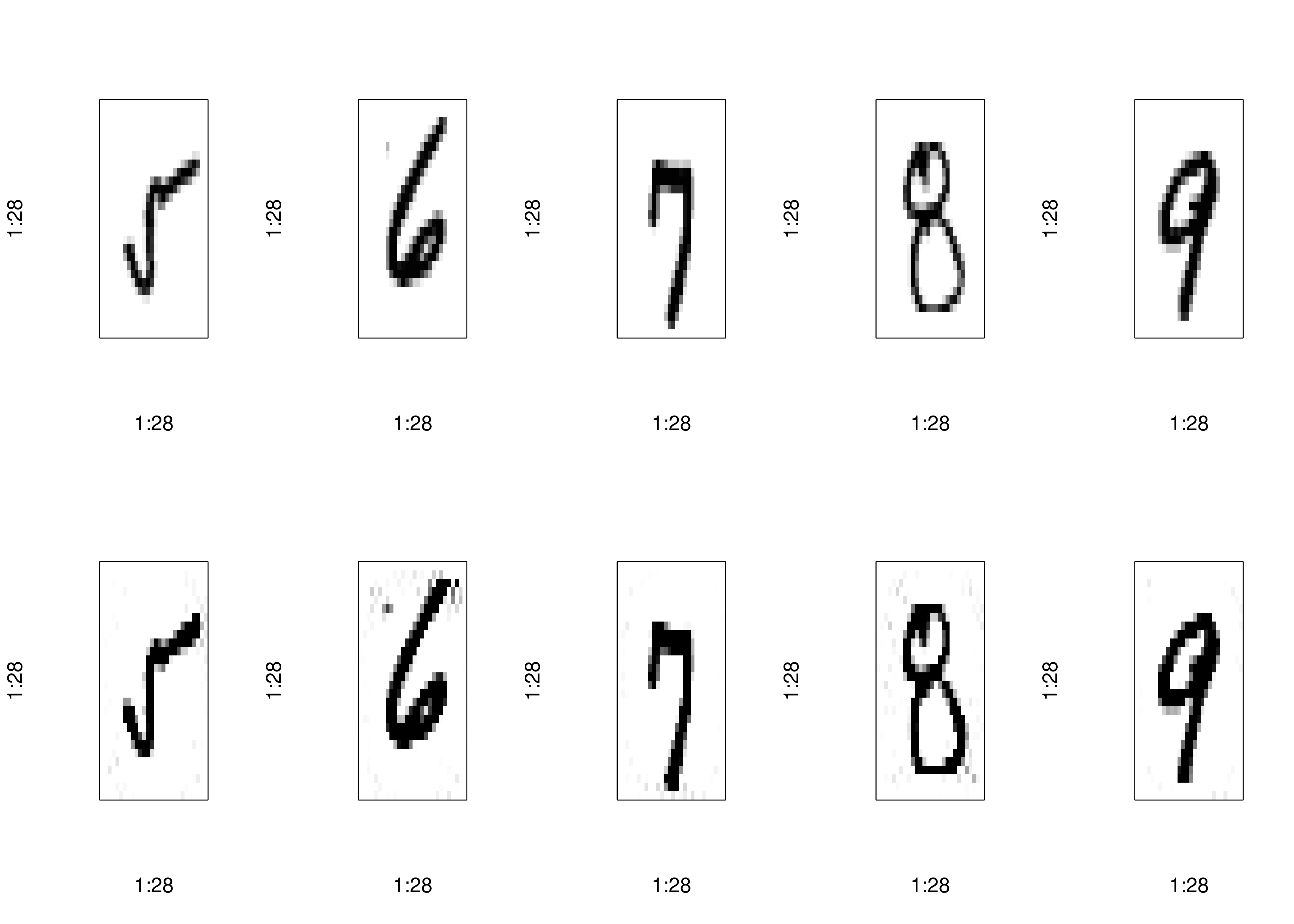
num_components <- 100
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[6:10])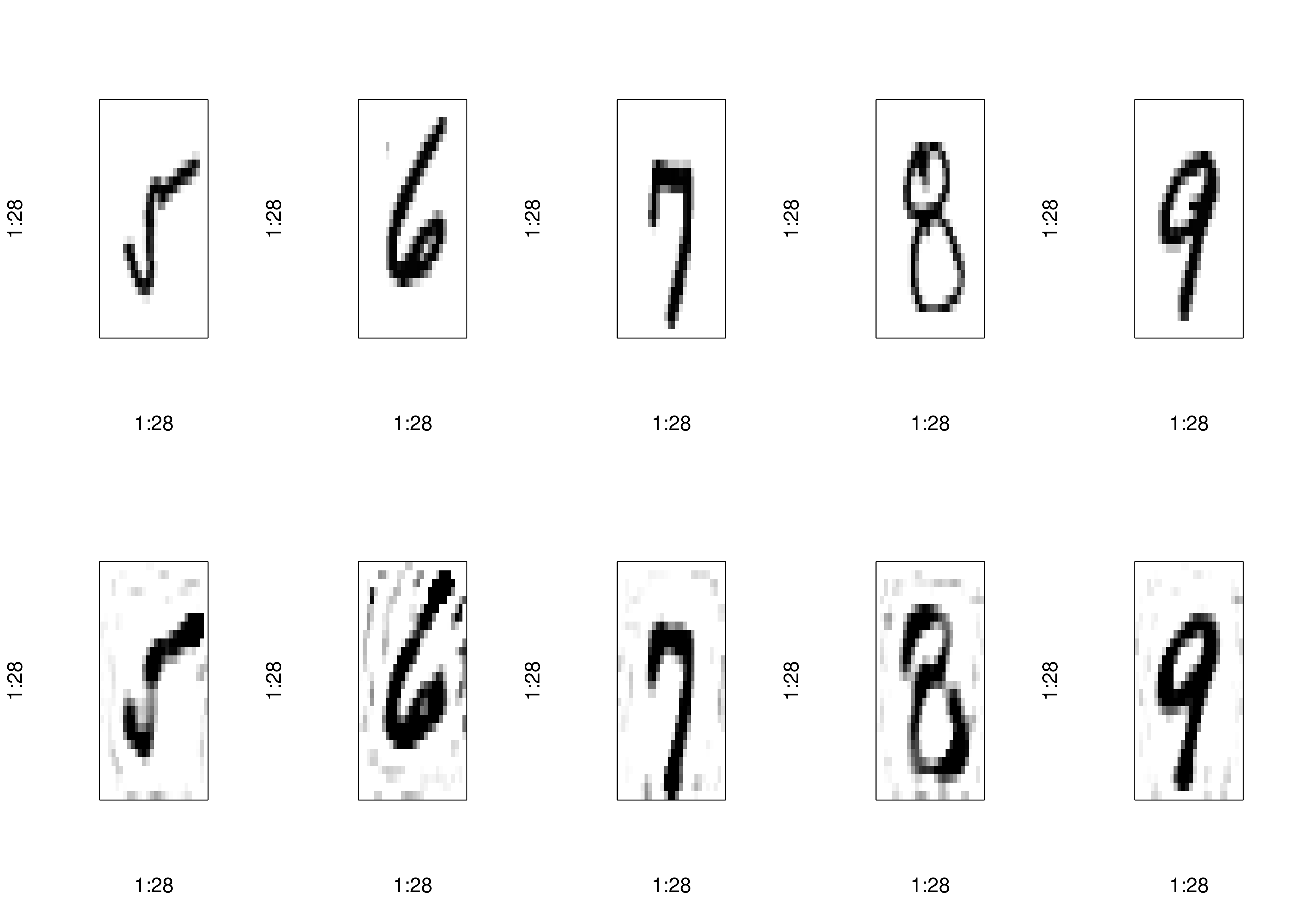
num_components <- 25
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[6:10])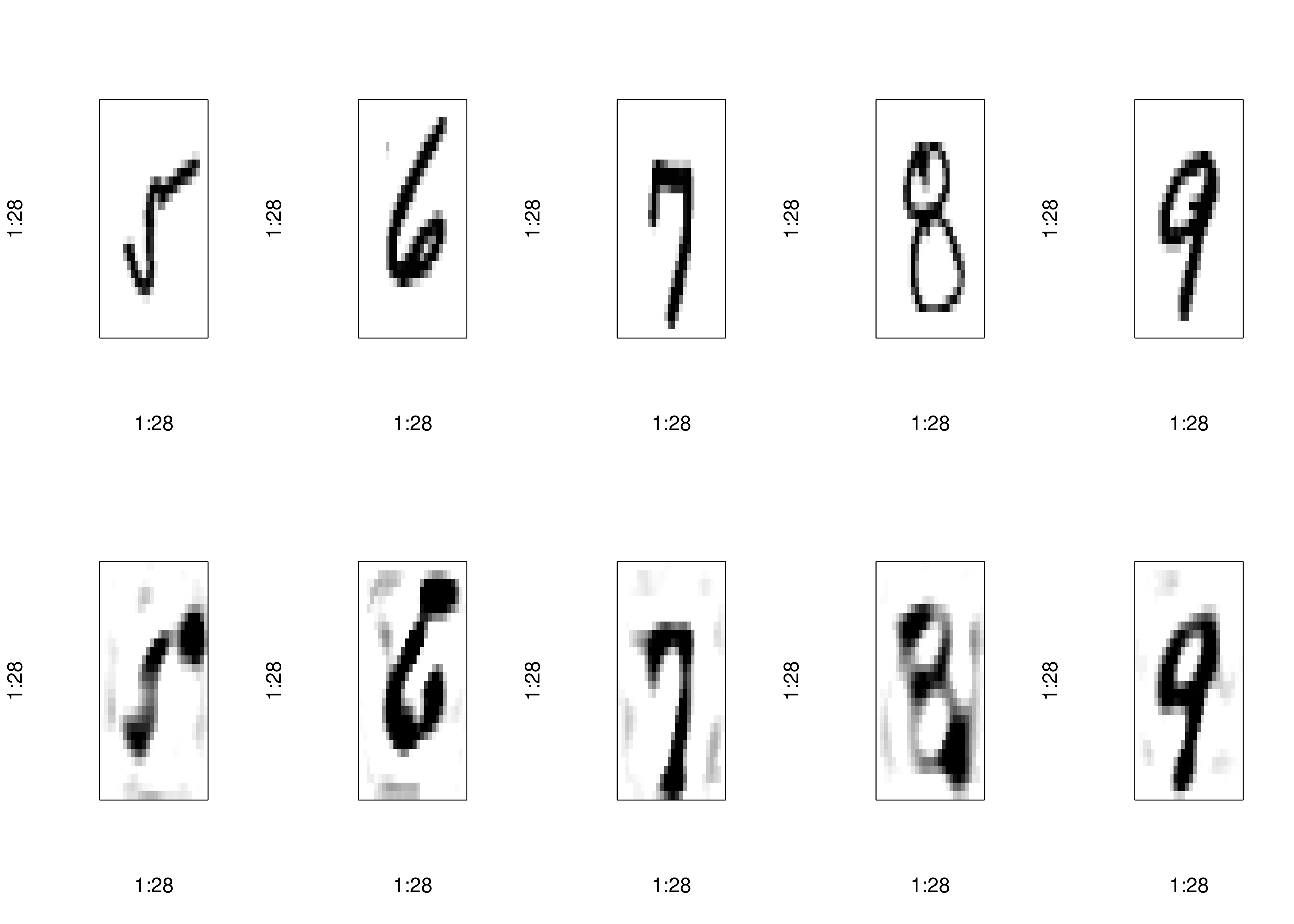
num_components <- 10
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[6:10])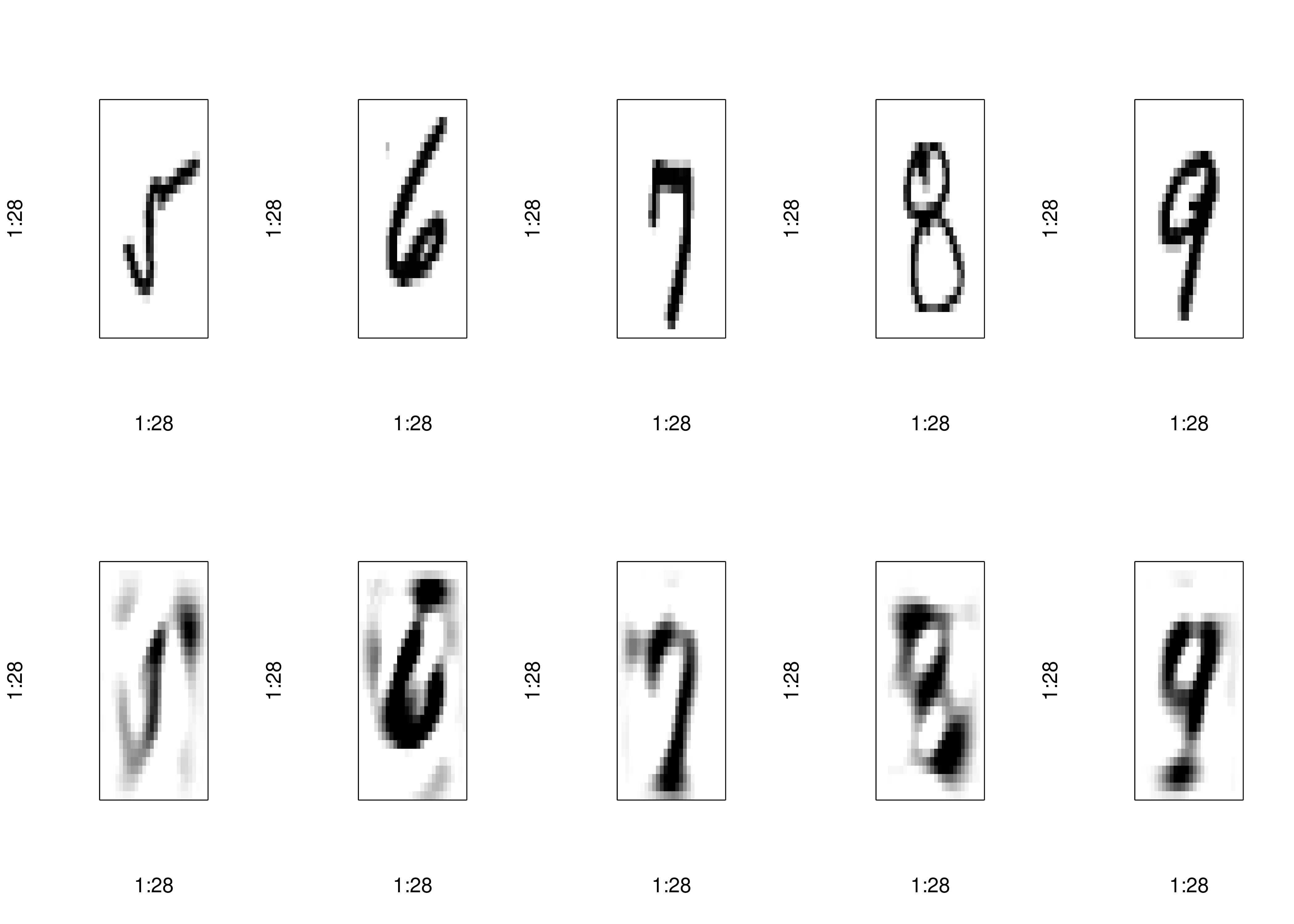
num_components <- 5
reconstructed <- pca_autoencoder(pca_train_full, num_components)
plot_reconstructions(x_train, reconstructed, indices[6:10])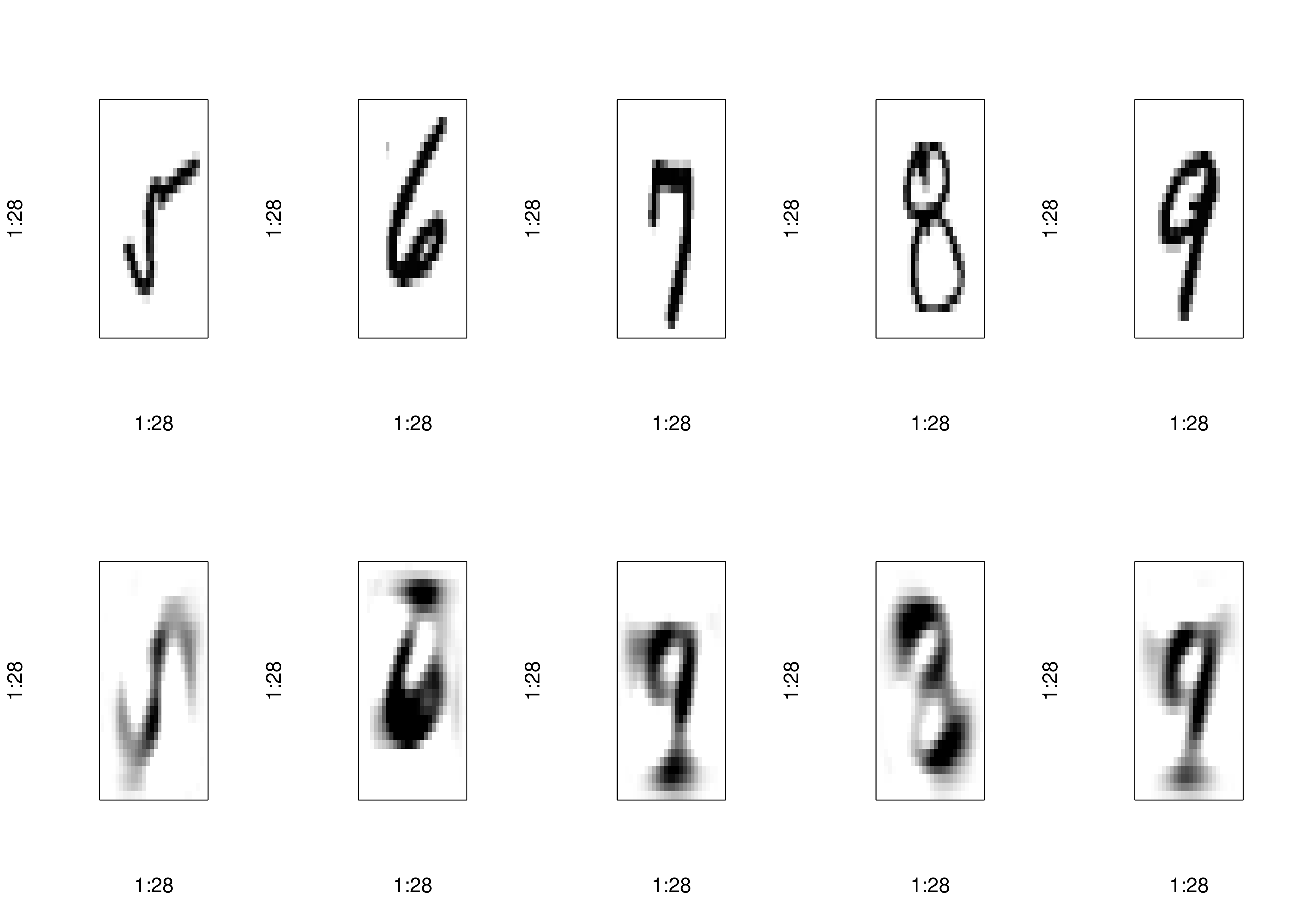
# Pull out the 4s and 7s
idxs <- which(y_train %in% c(4,7))
y_train <- y_train[idxs] == 7
x_train <- x_train[idxs,]
# Prepare validation data
idxs_val <- which(y_val %in% c(4, 7))
y_val <- y_val[idxs_val] == 7
x_val <- x_val[idxs_val,]
# Prepare validation data
idxs_test <- which(y_test %in% c(4, 7))
y_test <- y_test[idxs_test] == 7
x_test <- x_test[idxs_test,]
col_std_devs <- apply(x_train, 2, sd)
pr_comp_train <- prcomp(x_train)
# Print the first 10 digits in x_train
par(mfrow = c(2,5))
for (i in 1:10) {
plot_digit(x_train[i,])
}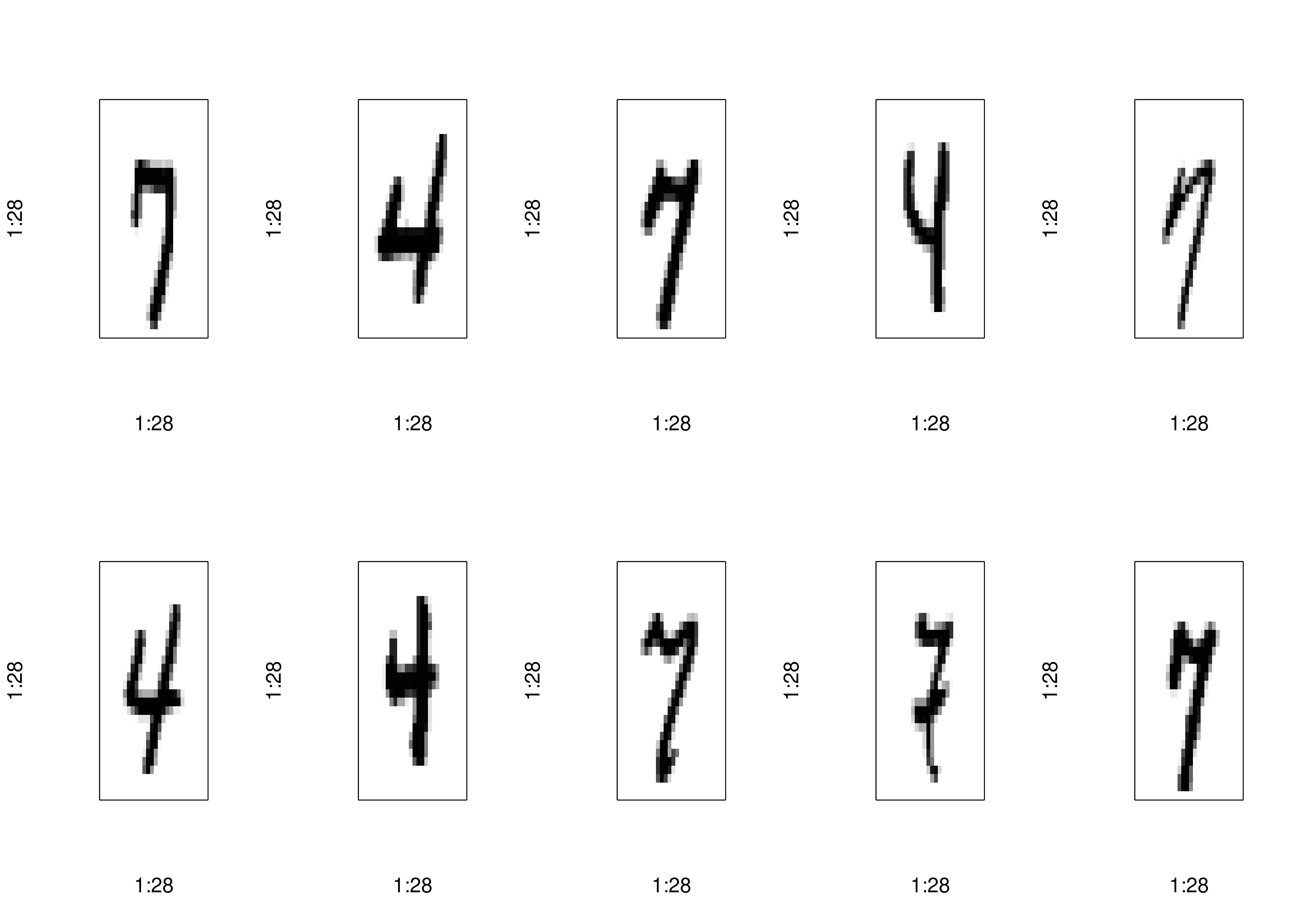
# Pull out the 4s and 7s
idxs = np.where(np.isin(y_train, [4, 7]))
y_train = y_train[idxs] == 7
x_train = x_train[idxs]
# Do the same for x_val, y_val, x_test, y_test
idxs_val = np.where(np.isin(y_val, [4, 7]))
y_val = y_val[idxs_val] == 7
x_val = x_val[idxs_val]
idxs_test = np.where(np.isin(y_test, [4, 7]))
y_test = y_test[idxs_test] == 7
x_test = x_test[idxs_test]
col_std_devs = np.std(x_train, axis=0)
pca = PCA()
pr_out = pca.fit(x_train)x_train_filtered <- as.data.frame(x_train[, col_std_devs > 0])
x_val_filtered <- as.data.frame(x_val[, col_std_devs > 0])
x_test_filtered <- as.data.frame(x_test[, col_std_devs > 0])
logistic_model_varying <- glm(y_train ~ ., data=x_train_filtered, family = binomial)Warning: glm.fit: algorithm did not convergeWarning: glm.fit: fitted probabilities numerically 0 or 1 occurrednrow(summary(logistic_model_varying)$coefficients)[1] 629logistic_model_varying = LogisticRegression(random_state=0, penalty=None).fit(x_train[:, col_std_devs > 0], y_train)
logistic_model_varying.coef_array([[-3.44371486e-03, -5.06131406e-02, -4.10565964e-02,
-3.85641140e-01, -4.31010687e-01, -8.31775010e-02,
-4.72067017e-03, -6.98438318e-03, -1.98765062e-03,
-9.46529212e-03, -7.97468380e-02, -2.87914640e-01,
-5.53993674e-01, -5.12114662e-01, -5.63785968e-01,
-6.75695417e-01, -6.10629193e-01, -3.15071690e-01,
-1.35050965e-01, -1.91287560e-01, -1.58111693e-01,
-6.46574919e-02, -7.57262708e-02, -5.29818750e-02,
-6.34255828e-03, -2.41692053e-02, -2.79405385e-02,
-8.23091298e-03, 8.25295700e-02, 3.63677709e-01,
3.88197351e-01, 3.27761838e-01, 3.19613863e-01,
5.43150460e-02, -1.81851980e-01, 2.35377642e-01,
-3.91299881e-01, -6.34588103e-01, -7.15623537e-01,
-8.06742986e-01, -6.76583636e-01, -4.66282210e-01,
-2.17286884e-01, -1.22800888e-01, -6.37169584e-02,
-6.14113522e-03, -9.25438667e-03, 8.67069547e-02,
3.22695747e-01, 3.64158234e-01, 3.13114830e-01,
3.35491327e-01, 3.18594590e-01, 2.15241890e-01,
4.67925908e-01, 3.09473873e-01, 7.21797225e-02,
-3.10541736e-01, -5.41588331e-01, -4.79496508e-01,
-4.29546188e-01, -3.09058885e-01, -4.75791621e-01,
-6.67135557e-01, -6.84975229e-01, -2.45811195e-01,
-6.97224806e-02, -4.91403577e-03, 1.09170077e-02,
2.02135548e-02, -3.98313366e-02, -4.06066502e-02,
2.69923360e-01, 8.99337333e-02, 2.83298680e-01,
-5.13736514e-03, -3.19113839e-01, 1.30935915e-01,
6.40252634e-01, 5.33122475e-01, 5.00774514e-01,
2.71010496e-01, 3.29978436e-02, 1.28453610e-01,
3.90494956e-01, -5.08309125e-02, -3.80023387e-01,
-2.45496186e-01, -5.61053843e-01, -2.65227616e-01,
-7.77099305e-02, -1.18568814e-02, 4.38205661e-02,
1.98759726e-01, 9.59260023e-02, -3.12102186e-02,
1.86649422e-01, 7.56049106e-02, 5.42776807e-01,
2.19631144e-01, 6.55048348e-02, 4.95259193e-01,
4.65318490e-01, 5.76587125e-01, 9.22608755e-01,
6.93742777e-01, 9.89654802e-01, 1.00235522e+00,
5.60169794e-01, -8.99695851e-02, -2.21588406e-01,
-1.06840321e-01, -2.88768665e-01, -1.74652952e-01,
-5.98904933e-02, -7.78368618e-03, 3.43515616e-02,
4.94050875e-01, 6.17639182e-01, 5.79207213e-01,
8.16903580e-01, 4.10815266e-01, 4.49447403e-01,
1.42606257e-01, 2.94603196e-01, 1.07798947e-01,
-5.08142425e-02, 5.82551174e-01, 7.76678711e-01,
9.13287714e-01, 1.10128970e+00, 8.37499422e-01,
5.72953314e-01, -2.37120672e-01, 1.46792347e-02,
-1.06256216e-01, -1.92522473e-01, -2.76577767e-01,
-2.20288521e-01, -2.11769715e-02, 1.53826372e-02,
3.71279741e-01, 6.17774858e-01, 7.21874391e-01,
8.05797781e-01, 4.88789434e-01, 1.79057867e-01,
-1.73157788e-01, -1.95450334e-01, -4.81382140e-01,
-4.67344574e-01, 4.70965713e-01, 8.64618637e-01,
1.12444311e+00, 1.05264359e+00, 3.93002782e-01,
4.85341531e-01, 3.39100151e-01, 3.32681112e-01,
-2.11557818e-01, -1.60451936e-01, -3.23384222e-01,
-2.43668025e-01, -9.83460039e-02, 1.51626029e-02,
1.20415157e-01, 1.01904922e-01, 3.35348461e-01,
1.41077283e-01, 2.43966933e-01, -5.40311204e-02,
-9.36063667e-01, -4.46096296e-01, -4.55445928e-01,
3.46395391e-03, 1.05236767e+00, 1.26515215e+00,
8.17443972e-01, 4.49564872e-01, 5.79322070e-01,
7.73440173e-01, 5.68860268e-01, 3.15405894e-01,
2.73094722e-01, -2.40614349e-01, -1.31936458e-01,
-9.35318641e-02, -1.23792175e-01, 1.52842196e-03,
3.57920785e-02, 7.57036169e-02, 2.74612191e-01,
-2.81537005e-01, 7.34222564e-02, -1.91924126e-01,
-1.01473266e+00, -9.26802919e-01, -5.99675668e-01,
-3.44100229e-01, 1.23462131e-01, -1.45869908e-03,
-1.80187445e-01, 4.06545875e-01, 3.98732003e-01,
1.01203543e+00, 1.86644173e-01, 2.60630353e-01,
1.00176562e-01, -6.94092765e-04, 1.54919345e-02,
-1.27906458e-03, -6.87734291e-03, 1.68418590e-02,
3.09423068e-01, 1.82964337e-01, 3.36634909e-01,
-5.02394017e-02, -2.27761949e-01, -7.39432797e-01,
-1.13471546e+00, -1.43358703e+00, -9.02240191e-01,
-6.43276651e-01, -4.24776398e-01, -1.21330253e-01,
-3.89921434e-01, -1.21721898e-01, 8.80677043e-01,
2.81453721e-01, 3.01863718e-01, 3.30947280e-01,
9.69713756e-02, -2.02749358e-02, -4.57246521e-02,
6.63767356e-03, 1.68796988e-02, -3.06919709e-01,
-4.89338348e-01, -7.17717100e-01, -9.23706391e-01,
-9.45612640e-01, -1.13592347e+00, -1.45725682e+00,
-1.60336217e+00, -1.68649415e+00, -9.28955642e-01,
-6.68867637e-01, -7.27086288e-01, -1.62423244e-01,
4.01296451e-01, -1.74198729e-01, -1.17714547e-01,
7.09244207e-01, 7.47053361e-01, 4.98456846e-01,
-1.13553094e-01, -1.83623551e-02, -3.03668835e-03,
-4.88841551e-01, -4.95021302e-01, -5.06350202e-01,
-8.16009600e-01, -1.01985497e+00, -8.96971759e-01,
-7.70277120e-01, -1.17282684e+00, -1.34372632e+00,
-8.87229350e-01, -4.28012272e-01, -2.16910418e-01,
2.04183808e-01, 7.81080427e-01, 9.90227965e-01,
4.69685114e-01, 4.01459877e-01, 8.08015830e-01,
8.28142355e-01, 2.06175461e-01, 5.49445377e-02,
3.06853752e-03, -3.00908209e-03, -4.70636900e-01,
-4.38921647e-01, -1.01118574e-01, -2.86854217e-01,
-5.21523346e-01, -4.36489262e-01, -5.04522764e-01,
-8.24589051e-01, -6.20714333e-01, -4.36259116e-01,
-7.71929463e-01, -1.08245625e+00, -6.25499465e-01,
9.23119473e-01, 4.95819856e-01, -8.50328607e-02,
-1.79909286e-01, -2.13616135e-01, 3.19574568e-01,
8.18903658e-02, -1.16737525e-02, 4.49076198e-02,
-8.55794006e-04, -4.24867969e-01, -5.01954415e-01,
-1.45881426e-01, -7.14931522e-02, -1.24612036e-01,
-8.22319923e-02, -1.89987808e-01, -2.25149207e-01,
-4.97015949e-01, -6.77919837e-01, -4.83998928e-01,
-8.61298747e-01, -1.82023780e-01, 4.98093674e-01,
-3.51189085e-02, -3.00858984e-01, -4.58414932e-01,
-2.19748119e-01, 2.84686549e-01, -8.70742752e-02,
-4.91079832e-02, 1.47087140e-01, -4.23909691e-01,
-5.39635795e-01, -4.41721524e-01, -8.82155056e-02,
-1.29991893e-01, -4.96585745e-04, 1.91298450e-01,
-1.35832565e-01, -1.17927845e-01, 2.70271056e-01,
-3.57200536e-01, -5.55403966e-01, -2.77779786e-02,
-1.09219591e-01, -6.42359275e-01, -5.36117176e-01,
-3.32796965e-01, -1.12882084e-01, 1.31342370e-01,
-2.07832363e-02, -1.18494320e-02, -4.94045127e-02,
-4.68107050e-01, -3.35645612e-01, -2.75061741e-01,
-1.84315986e-01, 2.30148312e-01, 2.32622073e-01,
2.28127989e-01, 5.04280032e-01, 2.06076043e-01,
-4.56676626e-01, -5.83446757e-01, -1.86791814e-01,
-2.67722922e-01, -2.41560371e-01, -1.69234940e-01,
-1.97681596e-01, -1.44735568e-01, -1.03319452e-01,
-1.50015987e-01, -1.05862272e-01, -3.42812318e-01,
-3.28387332e-01, 3.52190945e-02, 3.24435265e-02,
-1.84394545e-02, 1.41920760e-01, 4.18236558e-02,
-2.87601347e-01, -4.21981400e-01, -6.14566871e-01,
-1.26072242e-02, 1.86642493e-01, 1.87871499e-01,
-4.49688699e-02, -3.15700476e-01, -4.70168130e-01,
-4.55517287e-01, -2.24429693e-01, 3.17227437e-03,
-5.78480784e-02, 8.31450493e-02, 1.57896049e-01,
1.68119615e-01, 1.44704731e-01, -2.32181579e-01,
3.23114964e-02, -1.65348492e-01, -4.81768528e-02,
2.22837560e-01, 2.20645907e-01, 3.02285660e-02,
2.57290041e-01, -1.80624109e-01, -5.28628988e-01,
-5.09455072e-01, -3.01092550e-01, -1.97431216e-02,
5.73715454e-04, 4.78849227e-01, 5.77908370e-01,
5.49406111e-01, 5.88599094e-01, 4.48041686e-01,
4.52773737e-01, 2.25512979e-01, 4.69691710e-01,
4.08193560e-01, 5.49618868e-01, 2.52396171e-02,
-4.42147844e-02, -6.34786446e-02, -2.10073976e-01,
-4.44571827e-01, -3.71321280e-01, -8.07027582e-02,
-8.33406253e-03, 3.54108216e-02, 5.33533281e-01,
6.13805303e-01, 3.70958661e-01, 5.06039613e-01,
6.56105401e-01, 4.58605772e-01, 5.14118223e-01,
5.21091522e-01, 1.22429245e-01, 5.23767298e-01,
-5.62584897e-02, -2.34823981e-01, -1.27809600e-01,
-9.96564871e-02, -9.02715119e-02, -3.25883791e-02,
-2.07556426e-02, -4.26704013e-03, 1.72114636e-03,
4.12655522e-02, 3.73797101e-01, 5.42173108e-01,
7.65763786e-02, 4.83646151e-01, 4.94702488e-01,
3.65434335e-01, 5.79848610e-01, 7.30011782e-01,
2.73982163e-01, 4.25204999e-01, 2.63058991e-01,
3.62179958e-01, 3.66192675e-02, -3.19994313e-02,
-8.69652178e-02, -2.51441230e-02, -1.05530139e-02,
-3.33362515e-04, 1.42711717e-02, 1.91733515e-02,
3.62766231e-02, 4.93359956e-02, -8.23276379e-02,
-1.25479182e-01, 2.43863943e-01, 6.98199054e-01,
8.62824788e-01, 6.48933238e-01, 2.81726283e-01,
3.45629116e-01, 3.21541088e-01, 8.23260442e-02,
2.29530872e-02, 3.13806764e-02, -9.74177598e-03,
-5.31087702e-03, 1.82871795e-02, 1.23348818e-02,
1.18630091e-02, 2.05903684e-02, 1.21628465e-01,
1.60572425e-01, 2.01539117e-01, 2.91040734e-01,
2.43222585e-01, 3.51812130e-01, 3.82830393e-01,
2.83961437e-01, 8.89264452e-02, 4.59230251e-02,
5.08985612e-02, 2.79865276e-02, 6.45179694e-03,
4.68784545e-03, 8.18057118e-04, 6.70806833e-03,
8.24601543e-03, 2.10268801e-03, 3.87131349e-03,
1.04261897e-02, 2.99938444e-02, 2.81283087e-02,
4.58866790e-02, 1.62881533e-02, 1.67672164e-03]])pca_train <- as.data.frame(pr_comp_train$x[, 1:50])
logistic_model_pca <- glm(y_train ~ ., data=pca_train, family = binomial)Warning: glm.fit: fitted probabilities numerically 0 or 1 occurredsummary(logistic_model_pca)$coefficients Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.198515947 0.21135576 5.67060924 1.422906e-08
PC1 3.647866454 0.19481760 18.72452246 3.124608e-78
PC2 -2.851327556 0.17512018 -16.28211881 1.322109e-59
PC3 -0.677184850 0.09516631 -7.11580437 1.112620e-12
PC4 1.637208408 0.12421894 13.18002196 1.143575e-39
PC5 0.077537401 0.12214106 0.63481847 5.255468e-01
PC6 -0.502354456 0.11548195 -4.35006906 1.360947e-05
PC7 0.792560391 0.11826262 6.70169838 2.060109e-11
PC8 0.351994691 0.11458539 3.07189847 2.127021e-03
PC9 -0.075791383 0.12492815 -0.60667978 5.440634e-01
PC10 0.008328826 0.14043146 0.05930884 9.527061e-01
PC11 0.128684822 0.14642117 0.87886762 3.794731e-01
PC12 -0.717080199 0.15831254 -4.52952237 5.911718e-06
PC13 0.278289184 0.16411883 1.69565667 8.995092e-02
PC14 -0.326632889 0.13879100 -2.35341547 1.860184e-02
PC15 1.260314977 0.22677140 5.55764509 2.734387e-08
PC16 0.517611645 0.19579969 2.64357748 8.203499e-03
PC17 0.203745210 0.17867643 1.14030267 2.541602e-01
PC18 -0.462318412 0.19603068 -2.35839822 1.835399e-02
PC19 1.687111767 0.21417667 7.87719665 3.348078e-15
PC20 0.464271371 0.19228580 2.41448599 1.575743e-02
PC21 -1.227411717 0.20335604 -6.03577694 1.581997e-09
PC22 -0.031785262 0.20788935 -0.15289510 8.784810e-01
PC23 -0.333466917 0.24870750 -1.34079960 1.799855e-01
PC24 0.331709788 0.21617545 1.53444707 1.249197e-01
PC25 0.626650997 0.25568504 2.45087077 1.425111e-02
PC26 -1.792752826 0.26452044 -6.77736968 1.223835e-11
PC27 0.471841396 0.23345342 2.02113724 4.326556e-02
PC28 -0.249239562 0.25586412 -0.97410906 3.300024e-01
PC29 0.991269359 0.23006621 4.30862643 1.642716e-05
PC30 -0.853862005 0.26247390 -3.25313109 1.141408e-03
PC31 -1.192374498 0.25172114 -4.73688668 2.170264e-06
PC32 0.486319978 0.28792777 1.68903464 9.121279e-02
PC33 -0.746747809 0.27508134 -2.71464359 6.634713e-03
PC34 0.184436366 0.28628786 0.64423398 5.194237e-01
PC35 -0.762210130 0.26286217 -2.89965700 3.735712e-03
PC36 0.491384339 0.29200836 1.68277492 9.241867e-02
PC37 -0.861588987 0.28665695 -3.00564484 2.650183e-03
PC38 0.069090777 0.31310575 0.22066276 8.253550e-01
PC39 0.331016384 0.29757616 1.11237535 2.659768e-01
PC40 0.442420067 0.31078038 1.42357787 1.545687e-01
PC41 -1.064491450 0.31896066 -3.33737542 8.457363e-04
PC42 1.334134332 0.33253726 4.01198455 6.021044e-05
PC43 0.434922210 0.34397461 1.26440207 2.060857e-01
PC44 1.554630008 0.33352244 4.66124567 3.143013e-06
PC45 0.642598732 0.31020298 2.07154271 3.830811e-02
PC46 0.072133706 0.33629020 0.21449839 8.301584e-01
PC47 -0.226714454 0.35323387 -0.64182535 5.209866e-01
PC48 0.095129357 0.34666329 0.27441428 7.837663e-01
PC49 -1.167863645 0.35342292 -3.30443662 9.516749e-04
PC50 -0.346077437 0.37424065 -0.92474572 3.550982e-01pr_out = pca.fit_transform(x_train)
logistic_model_pca = LogisticRegression(random_state=0, penalty=None).fit(pr_out[:, :50], y_train)
logistic_model_pca.coef_array([[-6.0753918 , 3.98708715, 2.05197569, -2.74121417, 0.86832373,
-0.4540733 , 1.6488431 , 1.66139935, 0.96397812, -1.11779385,
0.69926109, -0.04299947, -1.29184418, -1.08957067, -2.13875871,
-1.59027548, 0.56780922, 0.87858239, -0.23114992, 3.67962549,
1.38612478, 0.15315765, -0.23185715, -1.9792099 , -0.11281676,
1.2829825 , -2.10826642, 1.70570471, -2.72183216, -1.87313151,
-1.42228006, 0.10093863, -3.5761485 , -0.11095522, 0.07648331,
-2.9476521 , 2.27404433, -1.35848294, -2.50330241, -0.6200639 ,
0.97699899, -1.74761916, -2.11271925, -1.05139496, 0.24505012,
0.48072199, -1.31626291, 1.32579875, -0.90546252, -2.30792921]])# Perform PCA on the validation set using the same rotation from the training set
pca_val <- as.data.frame(predict(pr_comp_train, newdata = x_val)[, 1:50])
# Calculate accuracy on validation data
y_pred <- predict(logistic_model_varying, x_val_filtered, type = "response") > 0.5Warning in predict.lm(object, newdata, se.fit, scale = 1, type = if (type == :
prediction from rank-deficient fit; attr(*, "non-estim") has doubtful casesaccuracy_varying <- mean(y_pred == y_val)
y_pred <- predict(logistic_model_pca, pca_val, type = "response") > 0.5
accuracy_pca <- mean(y_pred == y_val)
c(accuracy_varying, accuracy_pca)[1] 0.9641089 0.9847360# Calculate accuracy on x_val/y_val
accuracy_varying = np.mean(logistic_model_varying.predict(x_val[:, col_std_devs > 0]) == y_val)
accuracy_pca = logistic_model_pca.score(pca.transform(x_val)[:, :50], y_val)
accuracy_varying, accuracy_pca(np.float64(0.9767631471667346), 0.9714635140644109)“A photograph, which used to be a pattern of pigment on a sheet of chemically coated paper, is now a string of numbers, each one representing the brightness and color of a pixel. An image captured on a 4-megapixel camera is a list of 4 million numbers-no small commitment of memory for the device shooting the picture. But these numbers are highly correlated with each other. If one pixel is bright green, the next one over is likely to be as well. The actual information contained in the image is much less than 4 million numbers’ worth-and it’s precisely this fact that makes it possible to have compression, the critical mathematical technology that allows images, videos, music, and text to be stored in much smaller spaces than you’d think.” Jordan Ellenberg
Note there are different ways to do this, but we ignore this subtlety in this course.↩︎