USArrests.hist <- hclust(dist(USArrests), method = "complete")
plot(USArrests.hist)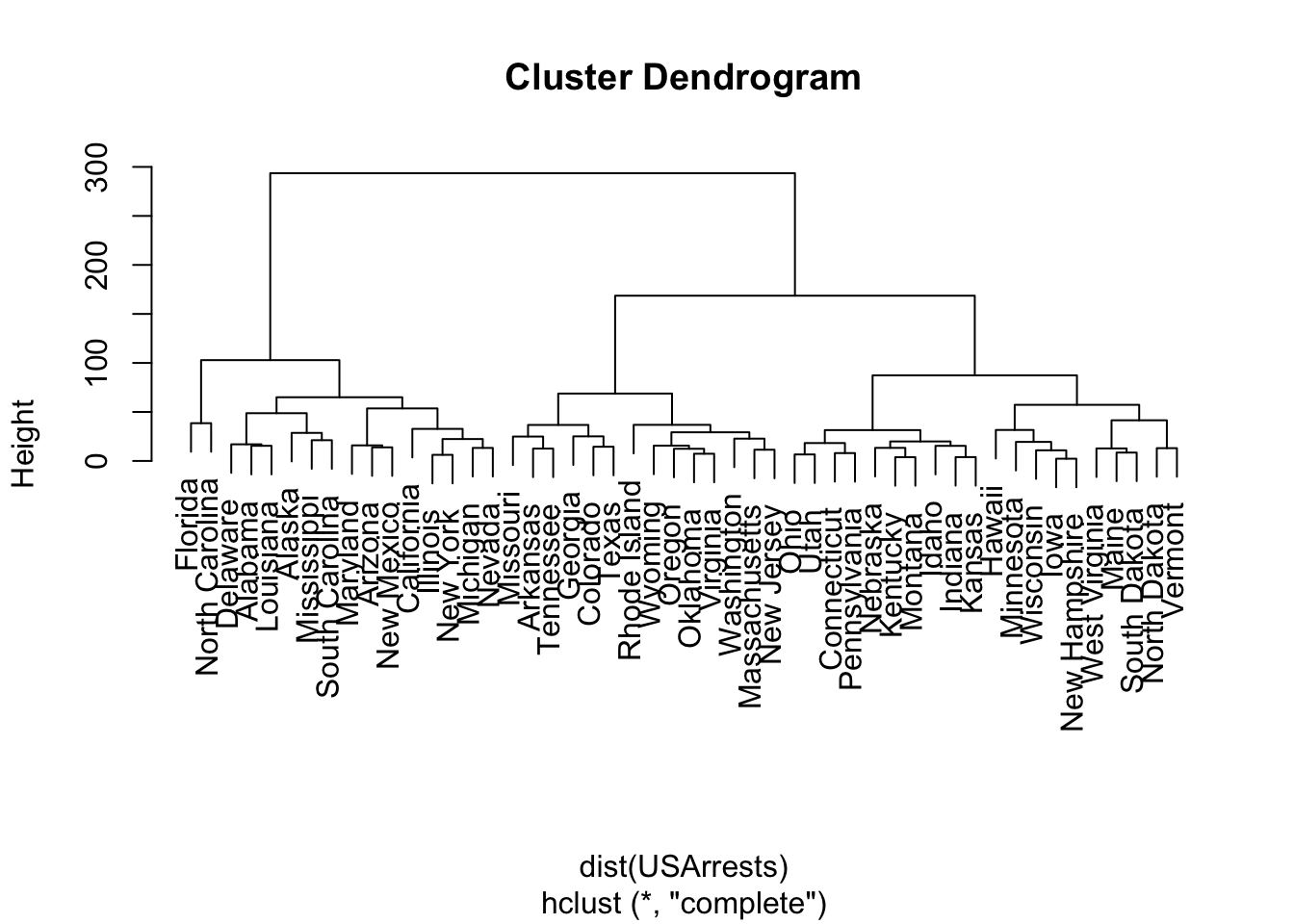
Lab 9: Clustering
Questions
Conceptual Questions
(ISLR2, Q9.2) \star Suppose that we have four observations, for which we compute a dissimilarity matrix, given by \begin{aligned} \begin{bmatrix} & 0.3 & 0.4 & 0.7 \\ 0.3 & & 0.5 & 0.8 \\ 0.4 & 0.5 & & 0.45 \\ 0.7 & 0.8 & 0.45 & \end{bmatrix} \end{aligned} For instance, the dissimilarity between the first and second observations is 0.3, and the dissimilarity between the second and fourth observations is 0.8.
On the basis of this dissimilarity matrix, sketch the dendrogram that results from hierarchically clustering these four observations using complete linkage. Be sure to indicate on the plot the height at which each fusion occurs, as well as the observations corresponding to each leaf in the dendrogram.
Repeat (a), this time using single linkage clustering.
Suppose that we cut the dendrogram obtained in (a) such that two clusters result. Which observations are in each cluster?
Suppose that we cut the dendrogram obtained in (b) such that two clusters result. Which observations are in each cluster?
It is mentioned in the chapter that at each fusion in the dendrogram, the position of the two clusters being fused can be swapped without changing the meaning of the dendrogram. Draw a dendrogram that is equivalent to the dendrogram in (a), for which two or more of the leaves are repositioned, but for which the meaning of the dendrogram is the same.
(ISLR2, Q9.3) \star In this problem, you will perform K-means clustering manually, with K = 2, on a small example with n = 6 observations and p = 2 features. The observations are as follows.
Obs X_1 X_2 1 1 4 2 1 3 3 0 4 4 5 1 5 6 2 6 4 0 Plot the observations.
Randomly assign a cluster label to each observation. You can use the
sample()command inRto do this. Report the cluster labels for each observation.Compute the centroid for each cluster.
Assign each observation to the centroid to which it is closest, in terms of Euclidean distance. Report the cluster labels for each observation.
Repeat (c) and (d) until the answers obtained stop changing.
In your plot from (a), color the observations according to the cluster labels obtained.
Additional Questions
\star In hierarchical clustering, two dissimilarity measures have been mentioned: Euclidean and correlation.
Consider two vectors \mathbf{x} = (x_1, x_2, \dots, x_n)^T and \mathbf{y} = (y_1, y_2, \dots, y_n)^T
Their Euclidean dissimilarity is: \left(\sum_{i=1}^n(x_i-y_i)^2\right)^{1/2}
For the correlation dissimilarity, we treat \mathbf{x} values as if they are from the same distribution X and \mathbf{y} values as if they are from the same distribution Y. Hence, there correlation dissimilarity is 1-\text{Corr}(X,Y)
Show that, in the case where \mathbb{E}[X] = \mathbb{E}[Y] = 0 and \sigma_X =\sigma_Y=1, correlation dissimilarity and Euclidean dissimilarity give the same results. (Use the population variance instead of the sample variance)
Provide a geometric interpretation of the correlation dissimilarity and the Euclidean dissimilarity. When would each be appropriate?
Applied Questions
(ISLR2, Q9.9) \star Consider the
USArrestsdata. We will now perform hierarchical clustering on the states.Using hierarchical clustering with complete linkage and Euclidean distance, cluster the states.
Cut the dendrogram at a height that results in three distinct clusters. Which states belong to which clusters?
Hierarchically cluster the states using complete linkage and Euclidean distance, after scaling the variables to have standard deviation one.
What effect does scaling the variables have on the hierarchical clustering obtained? In your opinion, should the variables be scaled before the inter-observation dissimilarities are computed? Provide a justification for your answer.
(ISLR2, Q9.13) On the book website,
www.statlearning.com, there is a gene expression data set (Ch12Ex13.csv) that consists of 40 tissue samples with measurements on 1,000 genes. The first 20 samples are from healthy patients, while the second 20 are from a diseased group.Load in the data using
read.csv(). You will need to selectheader = F.Apply hierarchical clustering to the samples using correlationbased distance, and plot the dendrogram. Do the genes separate the samples into the two groups? Do your results depend on the type of linkage used?
Solutions
Conceptual Questions
See Figure 1
Figure 1: The dendrogram from hierarchically clustering the four observations using complete linkage. See Figure 2
Figure 2: The dendrogram from hierarchically clustering the four observations using single linkage. (1,2), (3,4)
(1, 2, 3), (4)
See Figure 3
Figure 3: The dendrogram equivalent to Figure 1, for which two or more of the leaves are repositioned, but for which the meaning of the dendrogram is the same.
See Figure 4
Figure 4: The sample with n=6 observations and p=2 features. See Table 1.
Table 1: Randomly assigned cluster labels to each observation. Obs. X_1 X_2 Label 1 1 4 1 2 1 3 1 3 0 4 2 4 5 1 2 5 6 2 1 6 4 0 2 Label 1 X_1 = 2.67, X_2 = 3.00
Label 2 X_1 = 3.00, X_2 = 1.67
See Table 2.
Table 2: Cluster labels to each observation after one iteration. Obs. X_1 X_2 Label 1 1 4 1 2 1 3 1 3 0 4 1 4 5 1 2 5 6 2 2 6 4 0 2 See Figure 5
Figure 5: The final result of the K-means clustering.
Additional Questions
-
Breaking down the Euclidean dissimilarity: \begin{aligned} \sum_{i=1}^n(x_i-y_i)^2 &= \sum_{i=1}^n (x_i^2 - 2x_iy_i + y_i^2) \\ &= \sum_{i=1}^n (2-2x_iy_i) \end{aligned} Noting that 1 = \sigma^2_X = \mathbb{E}(X^2) - \mathbb{E}(X)^2 = \mathbb{E}(X^2) = \frac{1}{n}\sum_{i=1}^n x_i^2.
Now breaking down the Correlation dissimilarity: \begin{aligned} 1 - \text{Corr}(X, Y) &= 1-\frac{\mathbb{E}((X-\mathbb{E}(X))(Y-\mathbb{E}(Y)))}{\sigma_X\sigma_Y} \\ &= 1 - \mathbb{E}(XY) \\ &= 1 - \frac{1}{n}\sum_{i=1}^n x_iy_i \end{aligned} This is directly proportional to the Euclidean dissimilarity, and thus will give the same results (provided the method is linear in the way it summarises).Euclidean dissimilarity looks at how close the points are to each other in the parameter space, so if the data is clustered and related data tends to be of the same order of magnitude, this is appropriate. Correlation dissimilarity looks at how well the points fit on the same line. This is more appropriate if similar changes in features indicate similarity, despite the values being rather different.
Applied Questions
cutree(USArrests.hist, 3)Alabama Alaska Arizona Arkansas California 1 1 1 2 1 Colorado Connecticut Delaware Florida Georgia 2 3 1 1 2 Hawaii Idaho Illinois Indiana Iowa 3 3 1 3 3 Kansas Kentucky Louisiana Maine Maryland 3 3 1 3 1 Massachusetts Michigan Minnesota Mississippi Missouri 2 1 3 1 2 Montana Nebraska Nevada New Hampshire New Jersey 3 3 1 3 2 New Mexico New York North Carolina North Dakota Ohio 1 1 1 3 3 Oklahoma Oregon Pennsylvania Rhode Island South Carolina 2 2 3 2 1 South Dakota Tennessee Texas Utah Vermont 3 2 2 3 3 Virginia Washington West Virginia Wisconsin Wyoming 2 2 3 3 2USArrests.scale <- scale(USArrests, center = FALSE, scale = TRUE) USArrests.scale.hist <- hclust(dist(USArrests.scale)) plot(USArrests.scale.hist)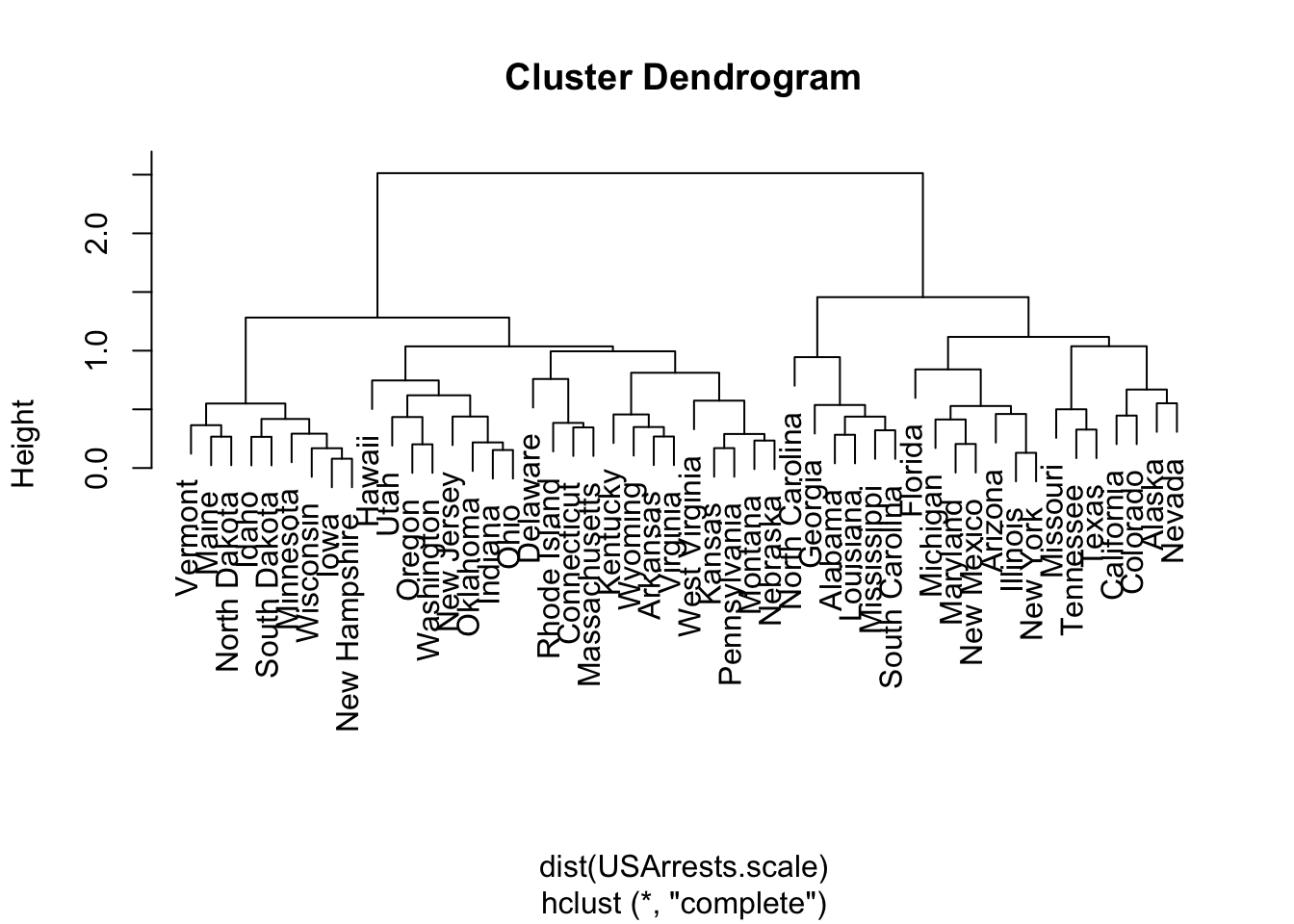
- Scaling reduces the effect of variables which have a significantly higher order of magnitude, especially since a Euclidean distance is used. This will cause some of the values to shuffle categories around the second-third level or lower, but the overall high-level structure remains about the same. Scaling should be used especially when a distance metric is used, since it ensures the values are comparable and have the same (null) unit.
# Note that you will have to download the csv file into your working # directory myData <- read.csv("Ch12Ex13.csv", header = FALSE)- We note that the splits are very clear for complete linkage. Try some of the other methods to see what they produce.
gene.cluster <- hclust(as.dist(1 - cor(myData)), method = "complete") plot(gene.cluster)